由式（2-1）～式（2-3）可看出，雷达接收的回波波前具有二次项相位及更高阶的相位项，将严重影响外差光电探测效率，其中二次项相位可通过接收望远镜离焦实现补偿。

图2-3为离焦望远镜的示意图。设望远镜目镜焦距为f1、物镜焦距为f2。望远镜物镜入瞳在物镜的前焦面，孔径光阑直径d2，孔径函数p（x，y）。望远镜出瞳在目镜的后焦面，孔径光阑直径d1。则望远镜的放大倍数为M=。望远镜物镜和目镜的离焦量为Δl，望远镜光程为l。目标散射点回波入射到望远镜入瞳面上的光束波前为e0（x，y），采用线性光学系统的衍射分析［4］，在望远镜出瞳面上的场强波前为

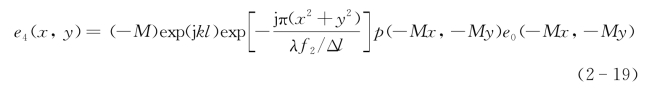
图2-3　离焦望远镜结构示意图

1）菲涅耳衍射波面补偿

对于菲涅耳衍射波面可以采用望远镜离焦方法补偿相位二次项，由式（2-1）和式（2-19）可以得到望远镜出瞳的光场为

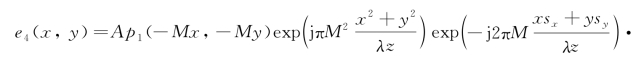
右边第一项p1（-Mx，-My）表示入瞳函数的缩小成像，第二项表示目标点衍射产生的波前二次项，第三项exp（-j2πM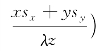表示目标点位置横向离轴产生的空间线性相位移，第四项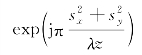表示目标点位置横向离轴产生的相位二次项延迟，第五项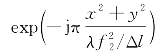表示望远镜离焦产生的相位二次项波前偏置。在逆合成孔径成像模式下，第四项是关键性因子，其是在接收过程中产生二次项相位的时间历程，用于激光孔径合成成像。

可通过控制第五项中离焦量补偿第二项的二次项相位，当离焦量为

可以消除入射波前的二次项，得到

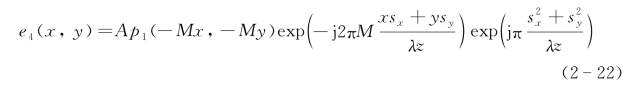
从上式可以看出，补偿后的目标回波光场仅包含目标点位置横向离轴产生的相位二次项延迟历程和线性相位项，该线性项影响了光学外差效率，应当小于光学外差接收机的接收视角所限定的最大线性相位。光学外差接收方向性函数表示回波光束相对于本振光偏角下的接收效率，其等效于接收口径的衍射极限方向性函数。

消除回波信号的衍射波面像差的另外一种方案是望远镜本身不离焦而采用出瞳补偿相位平板或者入瞳补偿相位平板进行等效离焦操作。采用望远镜出瞳位置上相位平板补偿时，其相位调制函数应为

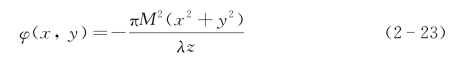(www.daowen.com)

采用望远镜入瞳位置上相位平板补偿时，其相位调制函数应为

2）夫琅禾费衍射波面补偿

对于夫琅禾费衍射波面可以采用望远镜离焦方法补偿相位二次项，由式（2-2）和式（2-19）并且通过

可以得到望远镜出瞳的输出波前为

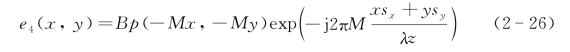
上式只存在目标点位置横向离轴产生的线性相位移，应当注意夫琅禾费衍射下不存在二次项相位的时间历程因子，不能实现孔径合成。此时也可以采用出瞳补偿相位平板或者入瞳补偿相位平板进行等效离焦操作。

3）瑞利-索末菲衍射波面补偿

由式（2-3）、式（2-19）并通过离焦调制控制可以消除入射波前的二次项相位，但是不能消除高阶像差。例如保留式（2-3）中的前3项，则有

可见第三项球面像差无法消除，是不适用的。

式（2-20）～式（2-27）中A，B和C为复常数。

4）讨论

目标处于菲涅耳衍射区域时可以采用离焦望远镜或等效相位板补偿回波波前二次项相位，保留目标运动产生的二次项相位历程；目标处于夫琅禾费衍射区域时可以采用离焦望远镜或等效相位板补偿回波二次项相位，但保留了目标运动产生的二次项相位历程；目标处于瑞利-索末菲衍射区域时不可能采用离焦望远镜补偿回波高阶像差，应当避免。

望远镜在不离焦的状态下也可以在望远镜之外采用光学系统或附件达到等效的离焦。有两种方法：一种是连接一个4f转像光学系统，其中间焦面离焦；另一种是对本振光束进行空间相位二次项偏置。

事实上，望远镜入瞳可以位于物镜前焦面的距离ΔL1上，则望远镜出瞳位于目镜后焦面的距离为ΔL2，有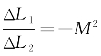，由此可以改变出瞳位置。光电探测器一般应当放在接收望远镜出瞳平面上，光电探测器可以离开望远镜出瞳平面一定距离，当光电探测器离开望远镜出瞳平面距离较大时应当采用转像光学系统。当光电探测器的输入端口为光纤时，光纤端面为光电探测器的等效感光面。