1.连续性方程和动量守恒方程

非压缩流体体积流动的质量守恒方程（尤其是两相系统）

其中，v指每相速度的加权总和（以固相体积分数f_s和液相体积分数f_L表示）

从方程（3-29）和方程（3-30）可以得到一个特别有用的关系

体积流动是由一般动量守恒方程的典型形式得出

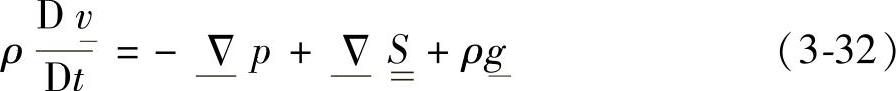
其中，

ρ=f_sρ_s+（1-f_s）ρ_L

式中 ρ——合金密度；

p——各向同性压力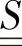；——附加应力张量；

g——重力加速度。

合金被当做不可压缩非牛顿流体：

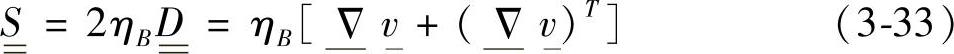
其粘度与固相体积分数f_s和变量κ（代表着内部触变结构变量）有关。

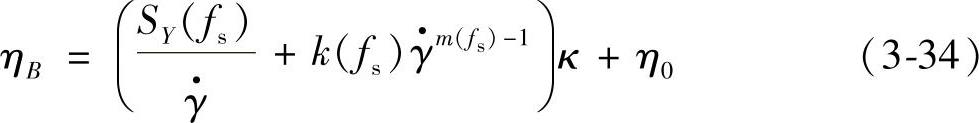
其中，

η₀=η_L（1+2.5f_s+14.1f²_s）（3-35）

粘度_η0指当κ=0时该半固态浆料完全解聚时的粘度。一般剪切速率定义为

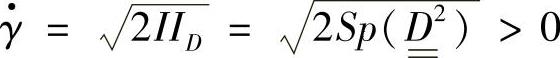
使用应变速率张量的第二不变量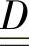，方程（3-34）中其他变量：S_Y（f_s），k（f_s）和m（f_s）分别是屈服应力、连续性和流动指数。由于很难确定全部的流变参数，通常方程（3-34）的最一般的形式是不适用的，对于一个典型的数值模型通常将方程（3-34）简化为以下方程

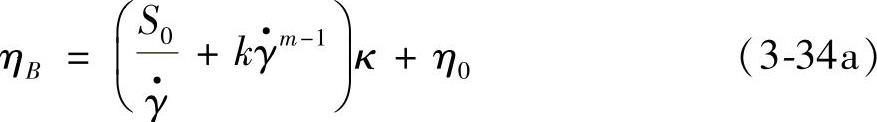
其中，S₀为屈服应力，k为连续性参数，m为流动指数，都是常数。方程（3-34a）代表当κ为常数时的各向同性结构流动。

对液相，动量守恒方程有下列形式

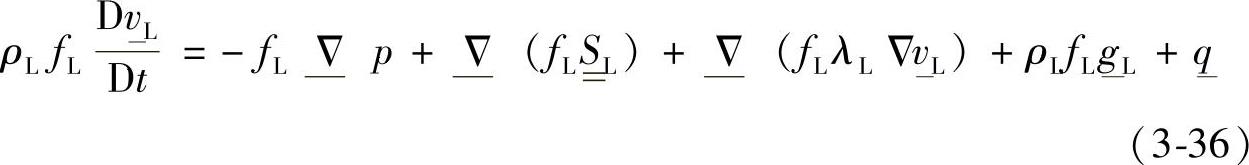
其中，

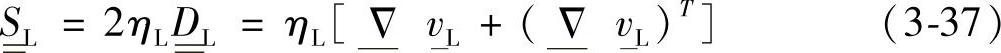
式中 ρ_L——液相密度；

p——各向同性压力；

液相流动的额外应力张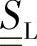——液相流动的额外应力张量；

η_L——常数（通常在0.02～0.025Pa·s，即牛顿流体）。

由于相间流动性的差别可能产生相分离，对于液相速度不一定等于零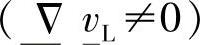的发散算子，液相被当做有效可压缩的对象来模拟。

这证明了方程（3-36）右边第三项所描述的这种有效压缩的发生，其中Lame系数λ_i用泊松比ν来表示

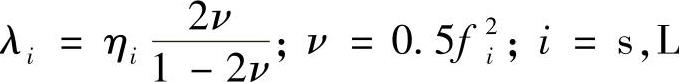
相界面摩擦力和滑移速度差成正比，阻力常数为C_Ls：

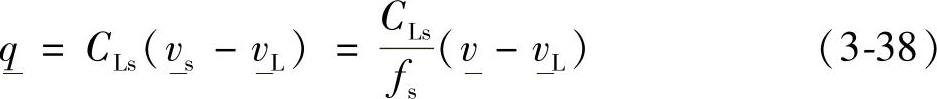
在高固相体积分数的情况下（0.5或更高，在相分离时可能会局部产生），阻力常数C_Ls很大，与之平衡的反压力梯度也会很大，在这种情况下，方程（3-36）可以有效简化为Darcy定律

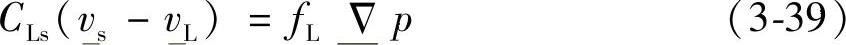
在这种状况中，C_Ls和固相渗透系数密切相关，通过Carman-Kozeny毛细管模型可以证明。在这一模型中，固相介质的孔隙与许多平行的毛细管系统类似。其关系可以在参考文献[37]中找到

其中假定f_s≥f_cr。临界值f_cr变化范围为0.4～0.5。另一方面，在低固相体积分数时的中间相阻力可用Stokes定律的适当形式表示

其中假定f_s≤f_cr。d_p为固相颗粒的平均直径，需在金相分析的基础上估值。

2.触变动力学方程

触变成形与时间密切相关，因此研究浆料流动模拟时触变模型很重要。这里介绍的触变模型来源于Moore^[38]经典方法，其中κ为结构参数，它表示集聚度，通常与剪切速率历史有关。其一般状态方程（如同方程式（3-34）中明确给出的）的一般形式为

结构参数的动力学变化（触变动力学方程），可按照下面的微分方程进行假设，即(www.daowen.com)

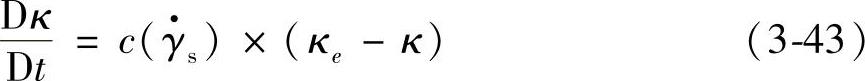
从上面方程明显看出，任何结构的变化都趋向于所谓的平衡结构参数所描述的平衡演化：

其中，n为所谓的平衡流动指数，将方程（3-44）用方程（3-44a）替代，得到

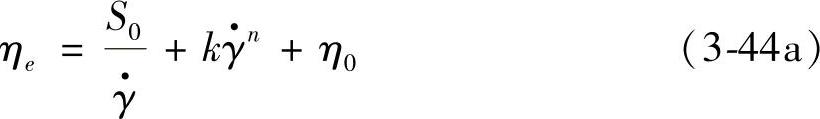
该式定义了所谓的平衡流动曲线，它代表流变平衡状态，理论上，经过很长时间以后可以得到。κ_e和η_e是与剪切速率有关的参数，因此，在任意流动过程中可能改变。

3.温度—焓的关系

在这里，热能守恒方程用以下形式表示

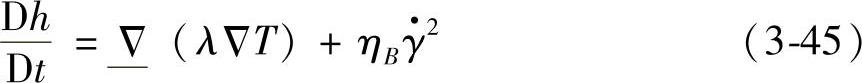
假定焓—温度之间存在一种独有的关系

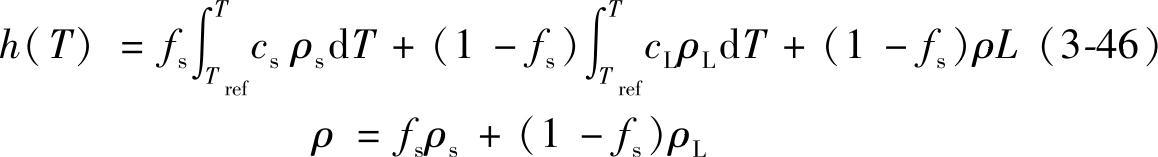
比热容恒定时，方程（3-46）可分解为如下的焓—温度公式

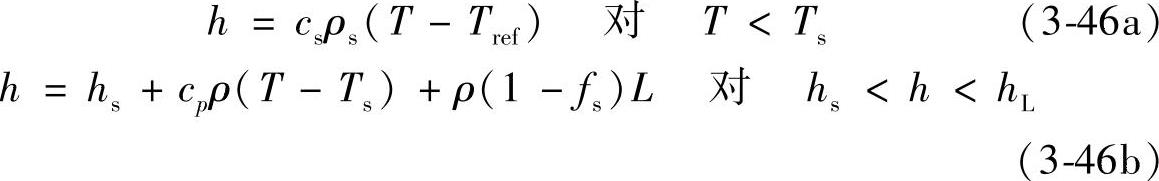
其中，h_s=c_sρ_s（T_s-T_ref）同时h_L=h_s+c_Lρ_L（T_L-T_s）+ρ_LL

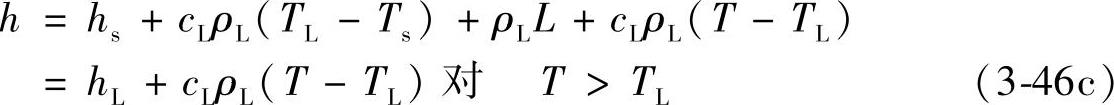
因此，以上关系可以用简明线性形式表示

A₁T+A₂h+A₃f₃=b （3-47）其中，

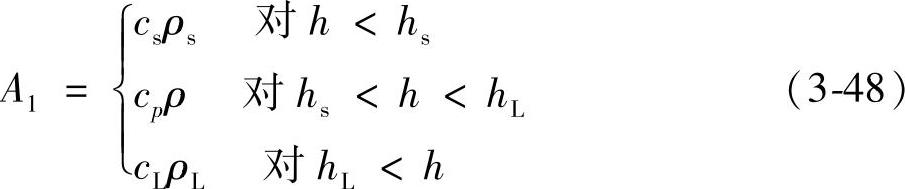
对纯金属：A₂=-1对熔体：

对纯金属，固相体积分数完全由焓决定，即

但是熔体在糊状时，固相体积分数f_s是独立变量。假定，固相体积分数变化时的动力学方程由其质量守恒方程决定，即

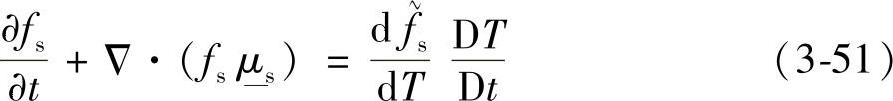
上式右侧表示相变速率，假定相变由Scheil方程描述的平衡状态决定，即

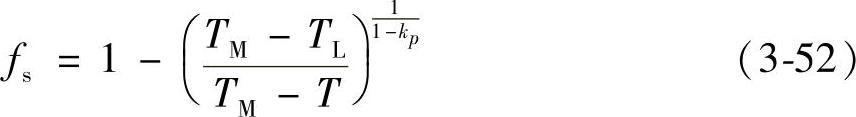
这样就得到右侧固相体积分数的一阶导数，即

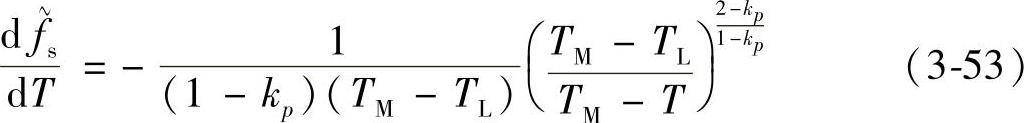
4.铝合金复杂零件触变成形的数值模拟

为了对上述数值模型进行验证，评价其对触变成形复杂形状零件的操作条件，本节对一实体模具进行了分析。典型零件选择的是由波兰WSK PZL-Reszow S.A.公司生产的汽车发动机支架，该零件原来由铝合金AlSi7Mg重力铸造而成，合金初始浇铸温度为700℃。在触变成形数值模拟模型中，初始温度设定为600℃；对于边界条件，温度设为255℃；对所有外表面速度矢量v=0，但对于入口表面速度设为5m/s。

使用商业软件ANSYS制作网格，然后通过专用的读入接口转变成模拟软件支持的格式，图3-16a表示了入口点和出口点以及热电偶的位置，该网格由四面体单元组成，节点和单元总数分别为6637个和24887个。

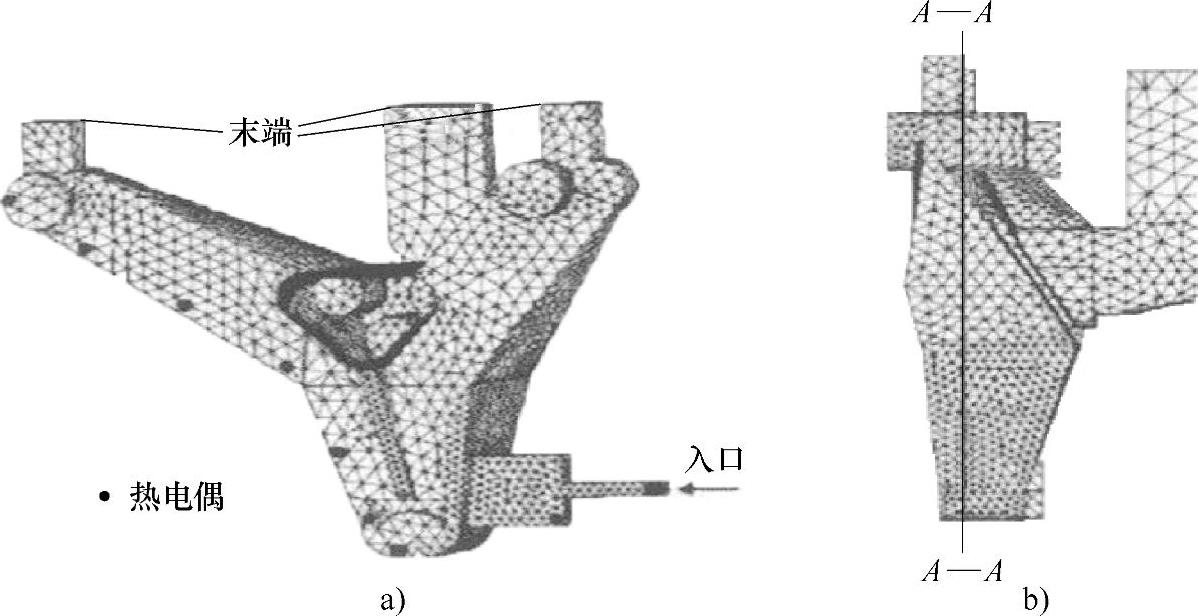
图3-16 汽车发动机支架的计算网格

a）热电偶位置 b）横截面图

瞬态触变成形过程的模拟使用了另一种由自己开发的模拟软件（时间步长和前面一样）。研究同时模拟了三个速度场（体积流动速度场，固相流动速度场，液相流动速度场）、温度场、焓场、固相体积分数分布场，模拟结果通过另一接口程序转化到商业软件FEMGV上展示。

图3-17表示该复杂零件触变成形的体积流动速度场，图3-18表示该复杂零件触变成形的压力场，计算的最大压力值为0.3×10⁸Pa（由于显示比例不均匀，不能直接从图3-18中看出）。因此实际半固态触变成形中施加的压力至少为30MPa。为了便于比较，图3-19表示重力铸造的压力场，其较好地反应了静水压力。

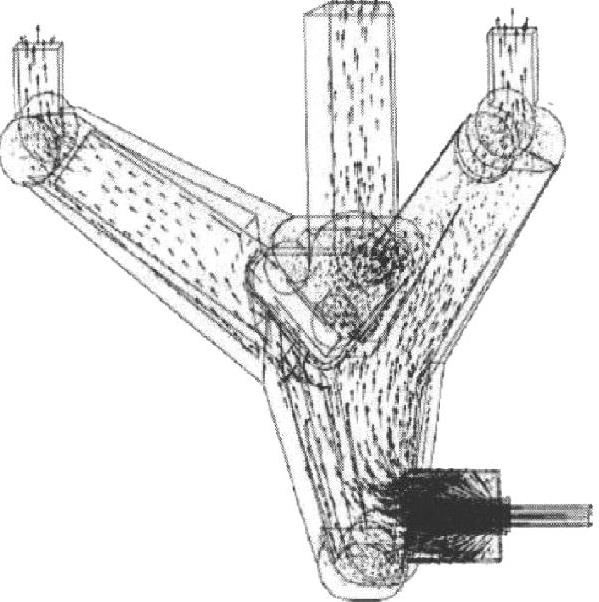
图3-17 复杂零件触变成形的 体积流动速度场

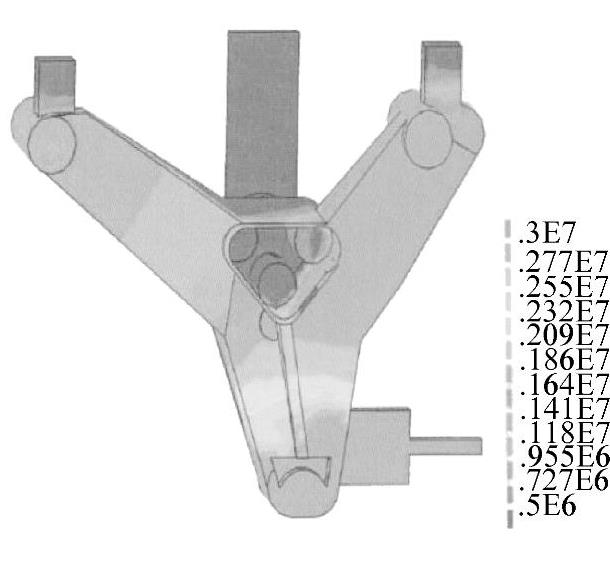
图3-18 复杂零件触变成形的压力场

图3-20用自由表面进程和相应的固相体积分数变化表示触变成形的不同阶段，其轮廓与图3-16a的横截面图相一致。观察可知，只要有合适的设备，则可以获得较好的充型能力。图3-21比较了热电偶测温的测试值和模拟值（起始的两个点被去除了，因为它们和所加的边界条件不相符）。观察发现，尽管测试值大多由边界条件而定，不过还是可以看到测试值和模拟值很好地吻合。

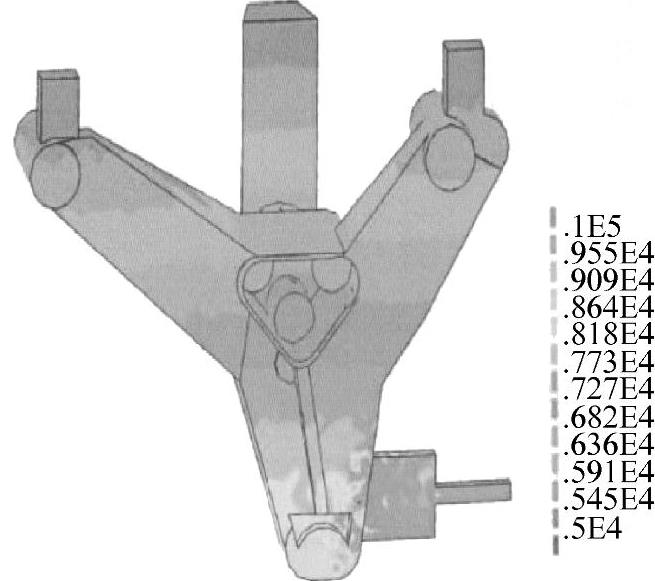
图3-19 复杂零件触变成形的静水压力场

数学模型是金属材料加工中热力学描述最常用的方法，包括应用于半固态加工中的触变成形技术。首先，考虑到液固相偏析和分离是半固态触变成形的典型特征，因此在半固态状态下应完全使用两相法来描述半固态浆料的流动。根据局部区域固相体积分数范围条件，使用Carman-Kozeny或the Stokes law模拟界面张力。第二，该模型能够反应与时间有关的现象如触变性，主要是由于在合金球状结构中发生了集聚。第三，用温度—焓—固相体积分数的关系同时描述非等温相变，提高计算各种场随时间变化的效率，特别包括在固定网格中对任意三维流动条件下的相变前沿追踪。

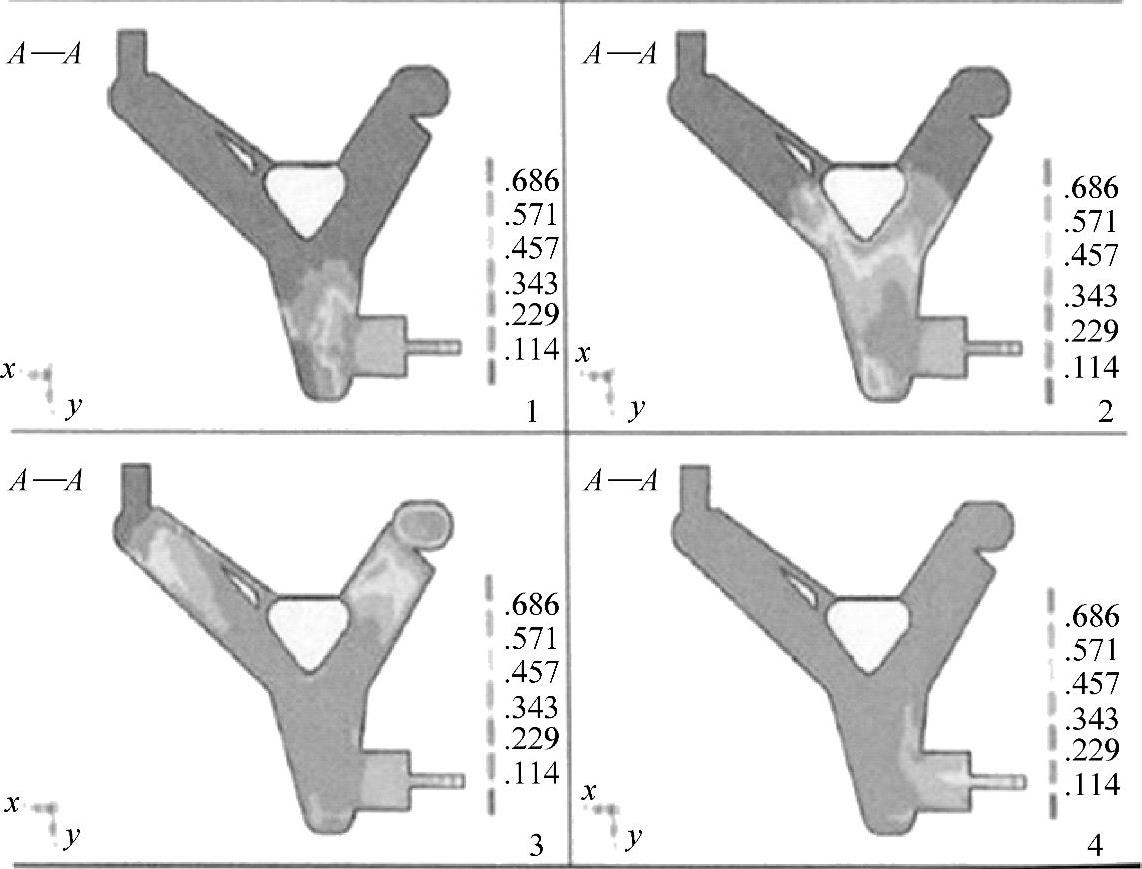
图3-20 用自由表面进程和相应的固相体积分数变化表示触变成形的不同阶段

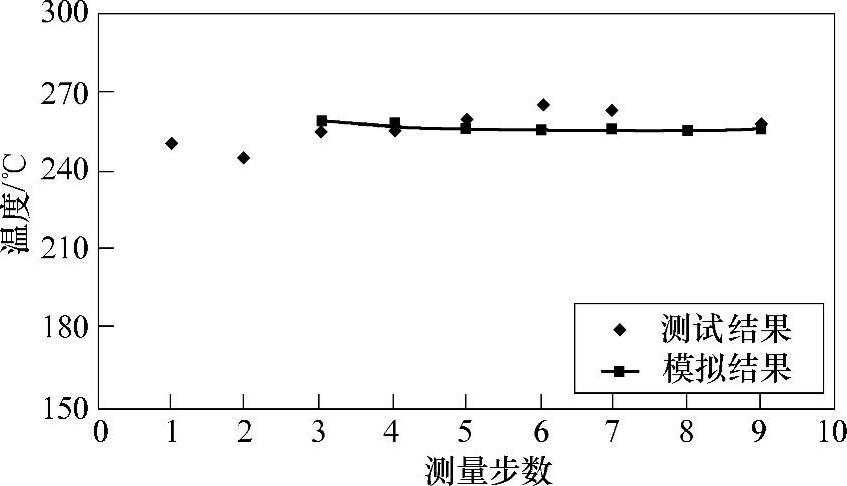
图3-21 热电偶测温的测试值和模拟值对比