在触变成形中，相分离是一个严重的问题，相分离的产生是由于在固液相线间的温度范围内同时存在液相和固相的不同流动性，通过在平行板间压缩圆柱件可以说明此问题。因为该试验设计几何结构简单，并且该试验已被很多研究小组详细的研究过，因此是一个非常理想的验证试验。例如：Chen和Tsao^[24]以恒定的应变速率压缩圆柱件，初始条件为：固相体积分数f_s=0.76，结构参数κ=1（完全“built-up”）。从图3-15可以看到，外部边界产生了相分离，为了对试验进行详细比较，对不同的应变速率给出了平均固相体积分数——相对半径比的曲线图。可以看出：由于液固两相的流动性不同，在圆柱件的外侧固相体积分数显然较低。

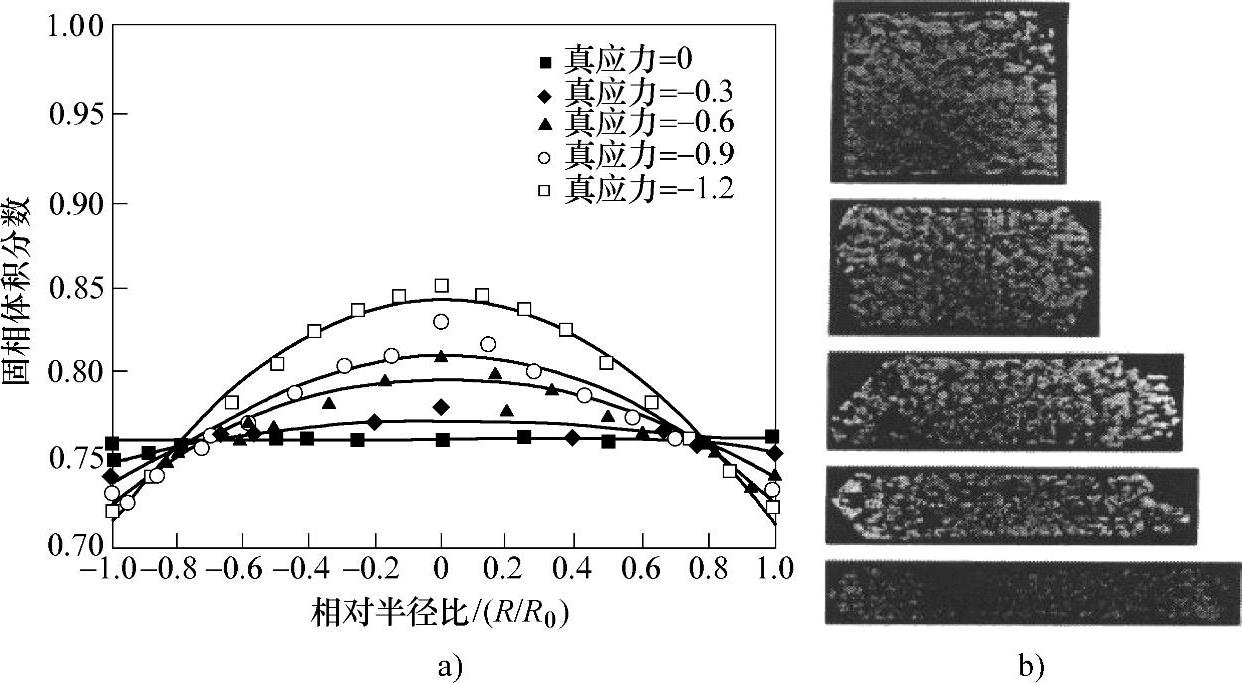
图3-15 压缩试验

a）固相体积分数与相对半径比R/R₀在不同真应变条件下的关系（应变速率为0.01/s，起始高度为10mm，起始半径为5mm） b）压缩时的组织变化

对相分离的解释有两种机理：向外的压力梯度和多孔固相的压缩性。考虑相分离就需用两相法，这里所讨论的两相法非常适合于等温条件下相分离过程的模拟，而非等温条件下该现象会进一步放大。因此，为节约试验经费，在试验之前可运用两相模拟进行过程设计。

由于在加工前需要准备坯料，因此触变成形技术与传统的金属成形方法相比具有本质的不同。触变成形在固液相线温度之间进行，且温度决定了被加工浆料的固相体积分数，因此对最终成形零件的质量来说，精确的温度设置最为重要。半固态金属材料加工时伴随着传热的进行，浆料中的化学成分发生分离，同时产生相变动力学、液相从界面前端扩散流失和对流混合。

在处理凝固/熔化问题时，其中一个最重要的技术是确定液固相界面位置随时间的变化。从数值稳定性的角度来说，只要相变在一定温度范围内发生，潜热充分释放的问题就容易解决。但是，等温相变时会有焓的突变，比热容经历狄拉克δ行为（Dirac delta behaviour），在极短的距离内释放潜热。从本质上来讲，存在两种模拟凝固过程的方法：第一种是在移动网格条件下使用前沿追踪法，第二种是在固定网格上使用前沿追踪法。前一种对简单问题的前沿可准确定位，但由于该方法涉及到可动的边界条件，其运用限制于一维或者界面已清晰界定的问题。后一种方法，通过焓来说明潜热的释放过程，且整个计算是在固定的网格上进行的。在固定网格法中，焓、比热容、虚热流和温度恢复技术都可以区别开。(www.daowen.com)

最常用的是有效比热容法，该法依赖于凝固前沿的焓梯度dh/dT的评价，可解决金属等温凝固和有限温度范围（糊状区域）凝固问题。然而，对金属等温凝固问题，需引入凝固时间间隔，但使用的时间间隔太长或者计算网格太大，则很可能会导致不能确定相变空间相应的前沿位置。另外一点是直接确定有效热容很困难，这与在凝固前沿相邻格点的步进行为有关。用迭代求解方法会产生数值波动，必须用一些平均化技术来处理这些问题。利用焓和温度的空间导数就可以准确确定相变点。虽然在相变中常使用焓梯度，但比热容在热能方程中使用还是比较普遍。为了避免数值波动，一般还会使用质量块。Sharma等[25]推出了另一种比热容方程改进法，来计算二元合金凝固过程中潜热释放问题，他们运用平衡关系或Scheil方程来确定相变速率。尽管仍然假定相变是以不同速率沿着相图中的平衡曲线进行的，但比热容方程改进法有时还是被错误地命名为非平衡的方法。

为处理相变过程的传热问题推出了一般焓法的不同变量。Swam-inatha和Voller^[26]引入了其中一个很有名的变量，他们用温度-焓关系来说明潜热的释放过程，原则上它只适用于合金和混合物^[27，28]。由于焓函数的不连续，为了消除等温凝固过程中焓值的突变^[26，29]，需对其取反函数。为了避免数值波动和更精确地模拟物理真实过程，Kim和Anghaie^[30]在通常的焓法中引入了一个有效传导长度模型，他们假设，相变单元边界的热流可以通过真实界面和相邻单元节点间距离来计算，而不是相邻单元间之间的距离来计算，将该方法运用到一维的金属等温凝固问题，发现它只适用于这种简单问题。

Swaminathan和Voller^[26]虽然提出了有名的逐步变化的温度-焓关系来处理纯金属问题，但将其运用到合金系统时，由于有很多常数，不能被普遍使用。特别是为适应非线性温度-焓的关系，需要进行长时间的迭代。Basu和Sekhar^[31]针对线性枝晶和等轴枝晶提出了一个凝固模型，他们假定在糊状区域液相体积分数—温度关系为线性，用线性的Scheil方程表示，但对于溶质含量低的合金却无效。

在解决凝固问题时，可使用许多数值方法，例如：流体体积元法^[32]、有限差分法^[33，34]和有限元法^{[26，35，36]}。

本节提出的凝固模型使用有限元法且适用于触变成形过程，该模型不仅涉及到热问题，更涉及到了半固态合金的流变性能。一种新的通用焓法变量已经被用在有限元算法中，使焓、温度和固相体积分数同时得到解决，这样就避免了为适应焓—温度关系来进行耗时的迭代过程计算。热能守恒方程（使用焓作为显式独立变量）与固相的质量守恒方程联立求解。其中后者涉及到Source/Sink因子，用以解释基于Scheil关系的相变速率。状态流变方程影响每一相的流动并反映了热量的变化。