在不可压缩半固态浆料(ρ=常量)中,对触变成形过程数值模拟的偏微分方程应用了质量守恒方程(3-14)(连续性),动量守恒方程(3-15)(重力是唯一有效作用力)和能量守恒方程(3-16)(针对非等温条件)。施加的外力包括模具内的压力和由附加应力张量 (方程3-15)表示的切应力。附加应力张量包括了所有关于半固态合金流动性能的属性信息,因此可以表示浆料的内摩擦。质量守恒方程
(方程3-15)表示的切应力。附加应力张量包括了所有关于半固态合金流动性能的属性信息,因此可以表示浆料的内摩擦。质量守恒方程 动量守恒方程
动量守恒方程
能量守恒方程
方程(3-14)至式(3-16)表明,通过速度矢量v将一系列微分方程联系起来。为了解决微分方程中大量的未知变量,必须有相应数量的偏微分方程用来求解。如果是等温状态,则方程(3-16)就不需要了,再将方程(3-14)、方程(3-15)转换为具体坐标系统(如笛卡儿坐标系),则未知变量就可以简化。如方程(3-16)和方程(3-17)可向坐标系中x向转变,未知变量写在了括号里。考虑到在y和z方向上总共加起来还有10个未知变量,即:压力、3个速度分量和6个附加应力张量。后者实际上是从角动量平衡得来的,要求切应力互等,即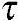 xy=
xy=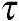 yx,
yx,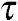 xz=
xz=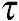 zx和
zx和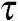 yz=
yz=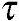 zy。
zy。
一系列紧密联系的偏微分方程最终通过应力—速度关系完成。通过半固态合金的粘度、应力张量S∗中的局部应力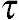 ij(i,j=x,y,z)与局部速度梯度联系起来(方程(3-19)),从而就可以获得剩下的6个方程(方程(3-20))。
ij(i,j=x,y,z)与局部速度梯度联系起来(方程(3-19)),从而就可以获得剩下的6个方程(方程(3-20))。
其中η——粘度(对半固态合金的流动特性进行模拟并计算获得); ——应变速率张量(i=x,y,z;j=x,y,z)。
——应变速率张量(i=x,y,z;j=x,y,z)。
式(3-19)中未知的η可以由表示金属悬浮液(浆料)流动行为的模型方法计算得出。
2.金属浆料的流动特性
由于半固态金属合金是由液相和悬浮在液相中的球状固相颗粒组成的,因此该浆料可以被当做如图3-6所示的经典悬浮液(半固态铝合金的结构和人工乳胶悬浮液)。悬浮液(浆料)的粘度与以下因子有关:固相体积分数、平均粒子尺寸、粒子尺寸的分布和粒子的形状,这些因子都影响浆料的流动阻力。此外,悬浮液(浆料)的流动性质还与其时间和应力历史有关。
图3-6 悬浮物
a)半固态铝合金的自由悬浮物b)人工乳胶悬浮物
半固态金属合金的典型流动特性就是剪切变薄和触变性,如果浆料静止还存在屈服应力,这都与其内部结构有关(即发生着固相颗粒的凝聚和解聚)。图3-7~图3-9给出了牛顿流体和半固态合金的流动行为的定性比较。图3-8b显示了剪切变薄浆料的典型粘度曲线,浆料粘度随剪切速率的增加而降低。图3-8a说明了在一定剪切速率下,随着时间的增加、粘度降低时材料的触变性。图3-9b给出了屈服应力存在时的流动曲线。
3.金属浆料的本构方程
图3-7剪切速率对不同流体粘度的影响曲线
a)牛顿流体 b)半固态合金
图3-8剪切速率一定时流体粘度随时间的变化曲线
a)牛顿流体 b)半固态合金(www.daowen.com)
图3-9屈服应力随剪切速率的变化曲线
a)牛顿流体 b)半固态合金
应力—速度关系的应用需要对以上试验所得的流动现象进行数值模拟,从资料上还可以找到其他不同的试验模拟结果。本节所讨论的公式见表3-1。
表3-1 金属浆料的本构方程
在20世纪初期,Einstein在半固态低体积分数情况下(fs<0.02)对牛顿流体进行了开发。Batchelor[11]和Thomas[12]等作者在Einstein方程的基础上对经验公式进一步发展,使其适用于较高的固相体积分数。为了说明固相粒子间的作用,他们引入了与固相体积分数fs有关的高阶因子。但是,以上两种都没有考虑剪切速率和时间(两者对半固态合金的流动特性很重要)的影响,表3-1中后三个方程考虑到了上述影响。
Ostwald-de-Waele关系式考虑到剪切速率的影响,切应力与剪切速率的n次方成正比关系,其中n为流动指数、k为稠度系数。当n=1时:Ostwald-de-Waele简化为牛顿方程(k=η);当n<1时,剪切变薄流体;当n>1时,剪切增厚流体。Herschel-Bulkley拓展了Ostwald-de-Waele公式用来描述存在屈服应力的流体,但McLelland[13]和Figuere-do[14]对于触变金属浆料是否存在屈服现象有争论。Barnes等[15-17]认为不存在屈服应力,他们认为屈服只是定义,不能测量;而Cheng[18]根据材料内部结构随时间的变化确定了静态和动态屈服应力,动态屈服应力逐渐增加直到达到静态屈服应力值(即内部结构完全build-up时的最大值)。
对以上所讨论模型的进一步发展是引入一个与时间有关的参数,该参数反映了半固态合金的触变性,Atkinson[19]总结了处理触变性的不同理论,它们主要是:
1)结构的build-up和break down程度是由一个标量参数来描述的。
2)直接描述微观结构及其随时间的变化(如固相粒子间大量的键)。
3)尝试使用粘度数据本身作为理论基础。
Koke等[20]提出的说明材料触变性的方法如表3-1中的最后一个。其中,κ是宏观结构参数,它包含与固相颗粒集聚状态有关的时间和剪切速率,当全部集聚时κ=1,当完全解聚时κ=0。
时间变化参数κ的定义如下:用速度常数c表示的一阶微分(式3-21),该方程需要结合质量守恒方程一起求解。
平衡时的结构参数κe根据方程(3-22)定义:
式中n——平衡态时流动指数;
m——在假定结构常数(表3-1中最后一个方程中κ=常数)下
描述流动特性的指数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






