通常将金属在半固态下根据其流动行为分为三种形式：①低固相体积分数状态（f_s＜20%）；②中等固相体积分数状态（20%＜f_s＜60%）；③高固相体积分数状态（f_s>60%）。当固相颗粒形成孔状实体时，半固态浆料可看成宏观组织是均匀的且各向同性的两相介质：整体的孔状实体和在实体中流动的液体组成，宏观变形必须与固相颗粒相协调^[9]。

在半固态流变成形的研究过程中发现，当剪切速率瞬间增加以后，浆料好像越来越厚。当合金的粘度降低到一稳定值时，浆料好像一剪薄的流体。粘度的大小主要取决于固相体积分数和剪切速率。在静止状态时，固相颗粒形成一骨架，它决定了半固态浆料的屈服应力^[1]。

根据M.Modigell等^[8]的研究，通常情况下，半固态浆料被认为具有非牛顿流体性能的均匀介质。其流变行为可用Herschel-Bulkley模型来表示

式中 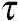₀——屈服应力；

κ——粘度指数；(www.daowen.com)

m——幂律指数。屈服应力和粘度指数可用与固相体积分数f_s相关的函数表示

式（3-12）中系数C₁、C₂和C₃可根据流变所测定的值进行调整。粘度指数κ表示了半固态浆料的悬液结构。浆料触变结构的动力学方程可用粘度指数κ的瞬间演变模型表示，通过对κ进行一阶求导得到下面的偏微分方程

式中 c——反应速度；

κ_e——在当前剪切速率下结构参数的平衡值。