如前所述，转子每一转出现的齿槽转矩基波周期数等于定子槽数Z和极数2p的最小公倍数N_c，即一个齿槽转矩基波周期对应的机械角θ₁=360°/N_c。因此，如果定子铁心斜槽角或转子磁极斜极角θ_sk和它相等，即可消除齿槽转矩的基波：

θ_sk=360°/N_c

对于整数槽电机，N_c=Z，斜槽角θ_sk：

θ_sk=360°/Z

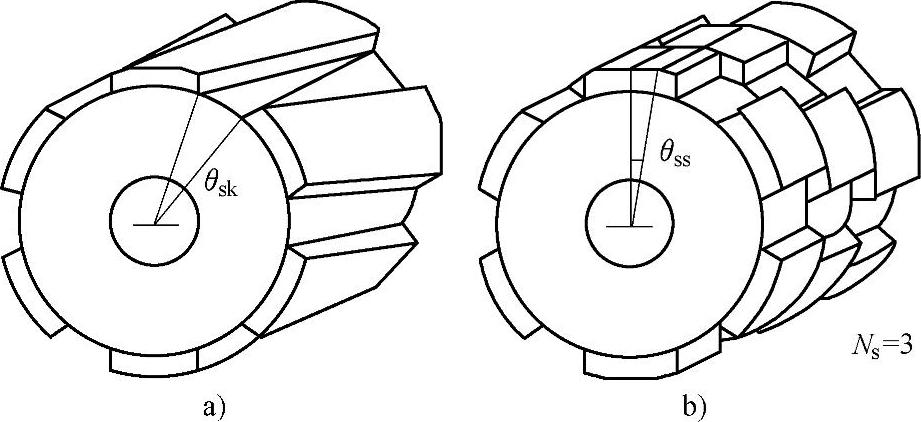
图10-13 转子斜极和转子磁极分段错位方法

看一个例子，一台Z=18，2p=6极的q=1整数槽电机，有N_c=Z=18，按上式，斜槽角度θ_sk为20°，即定子斜一个槽距，或转子斜极20°，见图10-13a，即可消除基波齿槽转矩。

但要指出的是，它同时会使反电动势和输出电磁转矩有所下降。定子斜槽还使绕组嵌线难度增加。而且，定子斜槽或转子斜极在电机绕组通电时，会产生附加的轴向力。轴向力大小与斜槽角度有关。

为了制造工艺上容易实施，可采用转子磁极分段错位方法近似斜极的效果，如图10-13b所示。该图是分段数N_s=3的情况。每段错移角度θ_ss表示为

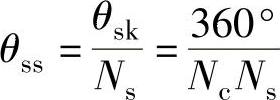
为了了解转子磁极不同的分段数N_s对降低齿槽转矩的效果，参考文献[5]用有限元方法进行分析计算，结果如图10-14所示。如图所示，随着分段数N_s增加，齿槽转矩的幅值逐步降低，而且当分段数N_s分别为2，3，4时，剩余的齿槽转矩变化次数增加，主要是2，3，4次谐波。从本实例可见，转子磁极分4段时降低齿槽转矩的效果已经很好，分段数为5时，齿槽转矩已经完全可以忽略了。

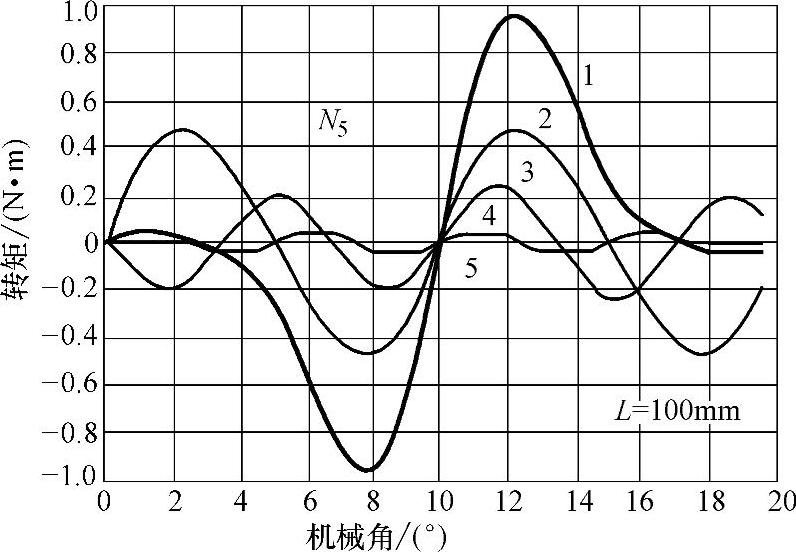
图10-14 转子磁极不同分段数的效果(www.daowen.com)

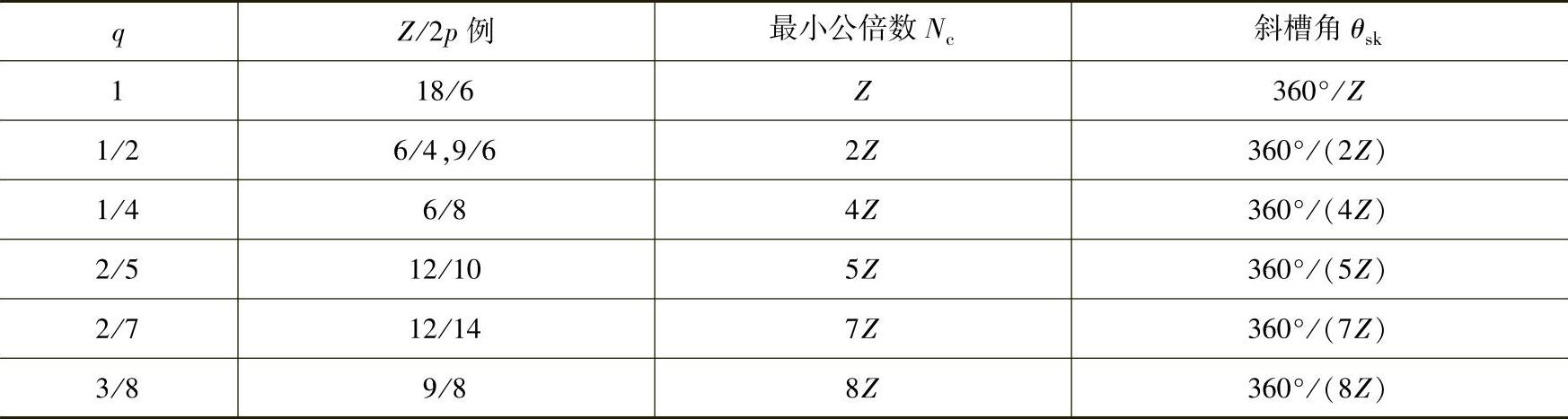
再来看分数槽情况。如前面分析，如果分数槽集中绕组的每相每极槽数q表示为q=c/d，则Z和2p的最小公倍数N_c=dZ。一些斜槽角θ_sk与q值关系例子见表10-8所示。斜槽角θ_sk与q值关系的一般表达式为

上式表明，对于分数槽电机，采用定子斜槽或转子斜极方法降低齿槽转矩时，定子斜槽角或转子斜极角小于一个定子槽距角，比整数槽电机小了许多，它们和q值有关，只需一个定子槽距角的1/d即可。所以，从斜槽工艺角度看，分数槽也是较好的选择。

从这个结论也可以引伸得：对于q有较大d值的分数槽集中绕组电机，定子直槽时的齿槽转矩已经不大了，甚至没必要采取定子斜槽角或转子斜极方法就能够适应大多数应用的要求^[12]。

表10-8 分数槽电机斜槽角θ_sk与q值关系例子

在图10-15给出对一台9槽6极电机（q=1/2）有限元分析的例子，得到在不同的定子斜槽角下齿槽转矩变化，由图可见，斜槽角20°或40°时，即斜半个槽或一个槽时，齿槽转矩最低。它与式（10-8）计算或表10-8结果一致。在图10-16还显示不同斜槽角与电机反电动势幅值关系。显然，取斜半个槽优于斜一个槽，对反电动势影响小一些。

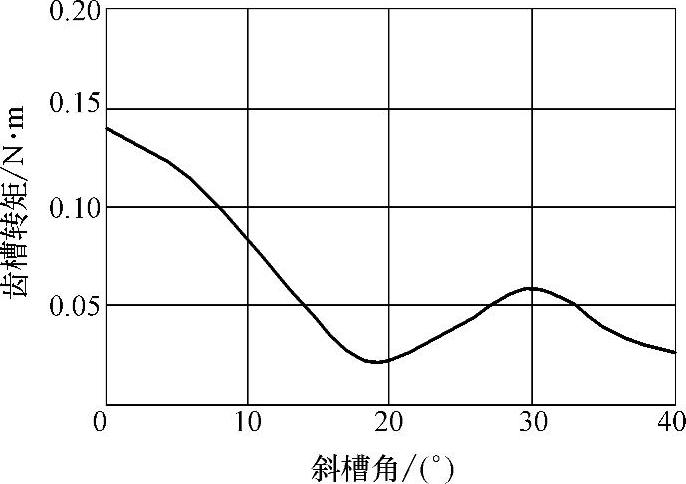
图10-15 一台9槽6极电机的斜槽角与齿槽转矩关系

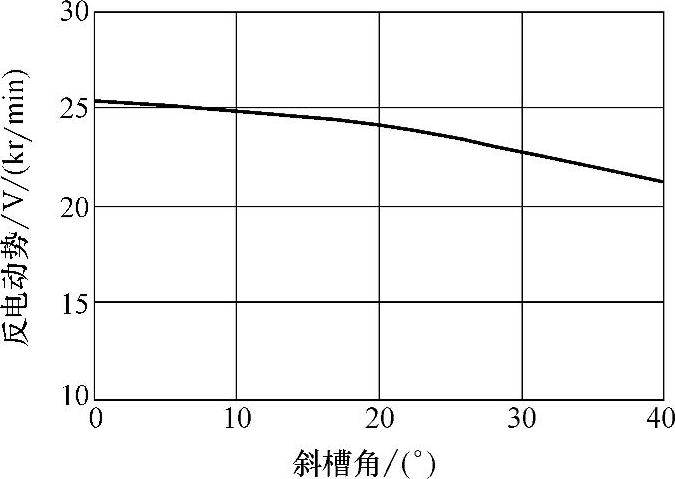
图10-16 一台9槽6极电机的斜槽角与反电动势关系

另外一个例子：分数槽电机Z=15，2p=4，q=5/4，有N_c=60，由d=4，利用式（10-8）计算斜槽角=360/（4×15）=6°。或由N_p=N_c/Z=60/15=4，即在一个齿距内平均有4个齿槽转矩基波周期，所以斜槽可以取一个齿距的1/4、2/4、3/4。最小的斜槽是1/4齿距，即6°，为最佳斜槽角。