转子磁极极弧宽和定子槽口宽是齿槽转矩很重要的影响因素。下面，极弧系数α_p是指磁极极弧宽和磁极极距之比，槽口系数β是槽口宽和槽距之比。槽口宽影响见第10.9节。

首先看整数槽电机情况。对于表面贴装的永磁磁极，如瓦形磁极，通常认为磁极极弧宽接近槽距的整数倍时有较低的齿槽转矩。如果以τ_s和τ_p分别表示定子槽距和磁极极距，最佳极弧系数可由下式给出：

上式可变换为

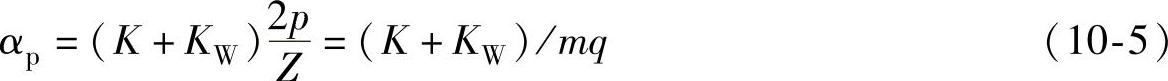
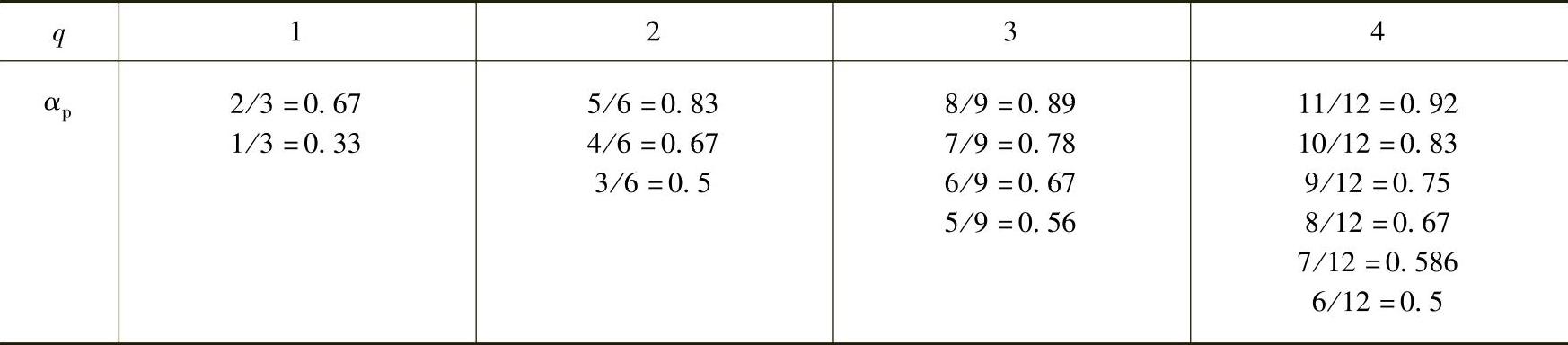
式中，K_W是修正系数，它与漏磁等因素有关。对于三相整数槽电机当不考虑修正时，取K_W=0，计算最佳极弧系数α_p结果见表10-5。

在参考文献[17]研究永磁体内置实心转子永磁同步电动机的齿槽转矩，提出了实心转子永磁同步电动机的齿槽转矩解析分析方法。其中以解析法分析并以有限元法验证了一台36槽6极电机，极弧系数为5/6时有较低的齿槽转矩。如果利用式（10-5）或对照表10-5，由该电机q=2，5/6是最佳极弧系数之一，说明计算结果与参考文献[17]分析结果一致。

表10-5 三相整数槽电机的最佳极弧系数α_p（设K_W=0）

考虑修正时，K_W的值有文献给出是0.14（1988年，Liao slemon），也有给出是0.17（1993年，Ishikowa和Liao slemon^[3]）。下面按0.17计算。对于常用的三相整数槽电机，由上式，q=1时，mq=3，最佳极弧系数为

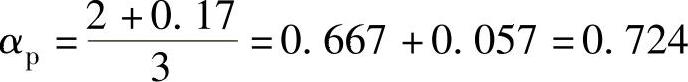
q=2时，mq=6，最佳极弧系数为

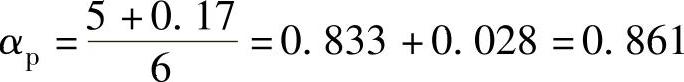
或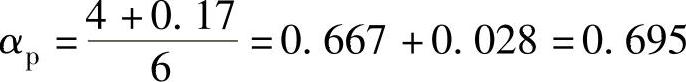

对于内置式永磁的情况，有文献对Z/2p=24/4，q=2的整数槽电机进行分析，如图10_-6所示，结构角θ_B2在35°～39°变化时，最佳角θ_B1是29.75°，即最佳极弧角约60°，最佳极弧系数约为60/90=0.67，与表10-5基本相同。从图10-6b可见，只要稍为偏离最佳极弧角，齿槽转矩就明显增大^[5]。

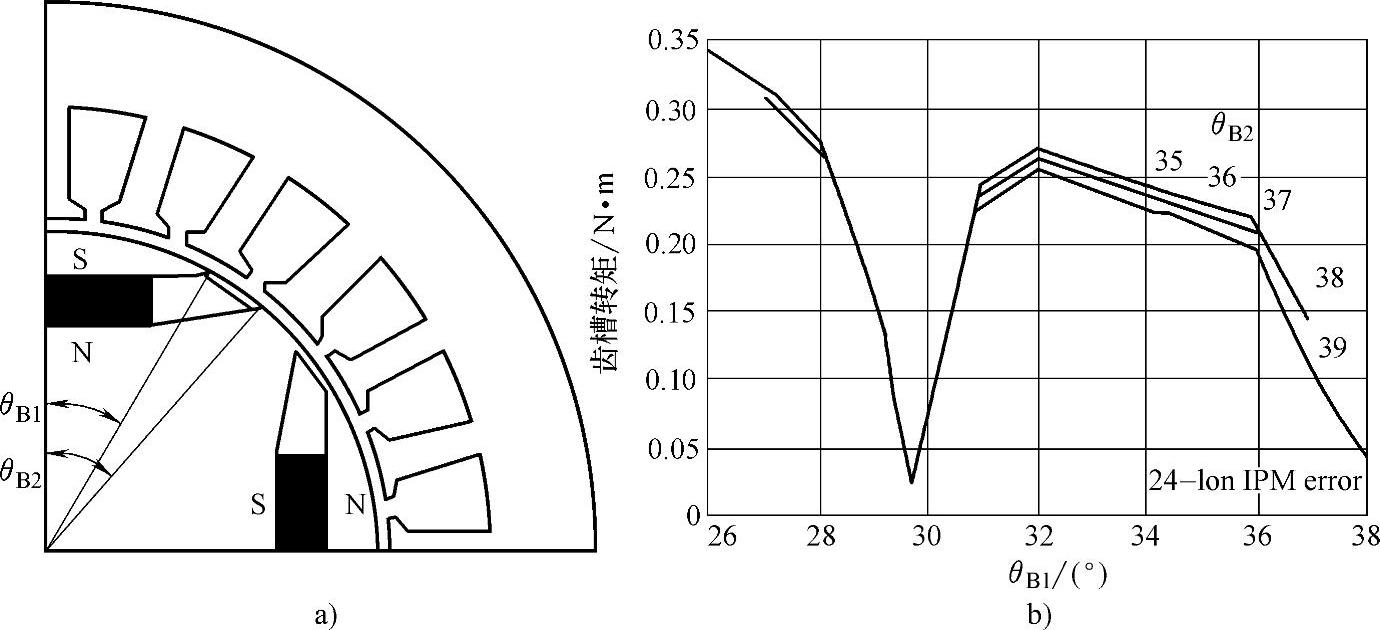
图10-6 永磁内嵌式4极电机齿槽转矩峰值与结构角关系

再来看分数槽电机情况，参考文献[2]提出，最佳极弧系数可由下式决定：

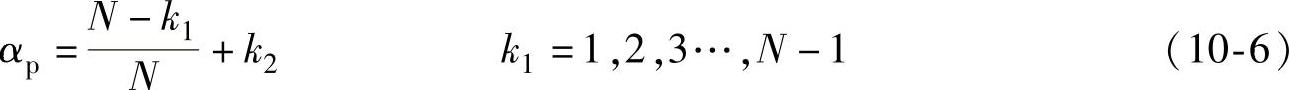
式中，N=N_c/2p，即平均一个极下基波齿槽转矩周期数，k₂是顾及磁极边沿漏磁的因数，和磁极间距、气隙大小等因素有关，可取0.01～0.03。设计时，为了获得尽可能大的气隙磁通而增加输出转矩，磁极弧长对磁极的比值应尽可能取得高一些，所以k₁宜取为1。

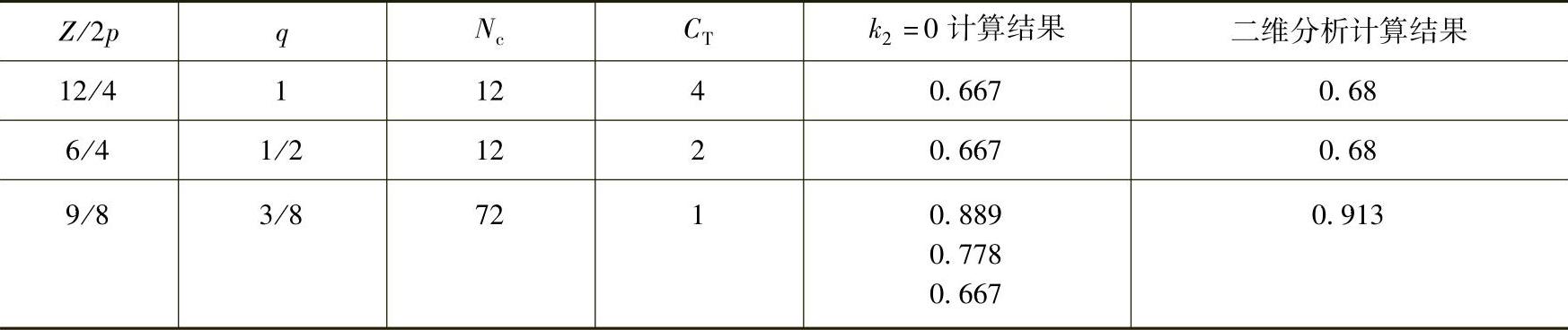
在图10-7给出三种槽数和极数组合的极弧系数与齿槽转矩峰值的比较，它们是利用式（10-6）尚未计及漏磁因数（k₂=0）时的计算结果。图中，Q_s为定子槽数，即Z。如果计及漏磁因数，采用二维有限元分析计算结果见表10-6所示，最佳极弧系数有所增大。

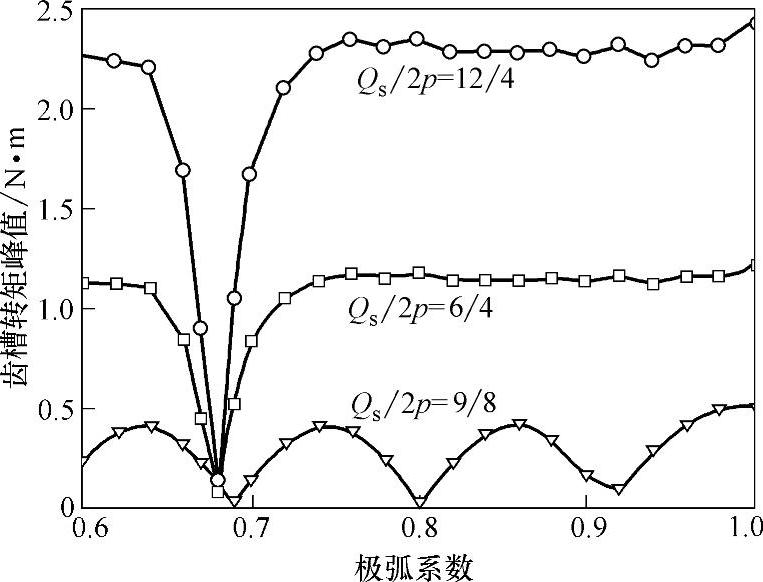
图10-7 三种槽数和极数组合的极弧系数与齿槽转矩峰值的比较

表10-6 三种槽数和极数组合的最佳极弧系数α_p

(www.daowen.com)

对于9槽8极无刷电机，当k₂=0，k₁分别取1、2、3时，利用式（10-6）计算得到α_p等于0.89、0.78、0.67为齿槽转矩低点对应的值。参考文献[14]采用有限元分析，借助Ansoft EM软件包中的Rmxprt模块和MaxweⅡ2D模块，应用场路结合对一台定子外径132mm铁氧体永磁9槽8极样机进行快速模拟和仿真。分析忽略漏磁和饱和的影响，求取α_p在0.6～1之间不同值的齿槽转矩。结果如图10-8所示。从图可以看出，齿槽转矩随着α_p的改变呈现近似周期性的变化，最低点分别出现在α_p接近0.89、0.78、0.67，与表10-6的k₂=0计算值吻合。从图还可以看出，如果稍微偏离这些点，齿槽转矩会有大幅提升。

在参考文献[1]第五章第2节专门讨论了基于极弧系数选择的齿槽转矩削弱方法，对永磁体剩磁通密度分布的傅里叶分解系数进行研究，分析它对齿槽转矩的影响。其中，对27槽6极电机例子进行分析，得到取极弧系数为0.667或0.777时，齿槽转矩应较小。如果我们利用式（10-6）进行计算，由N_c=54，N=N_c/2p=9，得到最佳极弧系数是α_p=0.889，0.778，0.667…。计算结果与参考文献[1]分析结果一致。文中另一个例子，30槽6极电机分析结果，当极弧系数为0.6或0.8时，齿槽转矩应较小。同样，如果我们利用式（10-6）进行计算，由N_c=304，N=N_c/2p=5，得到最佳极弧系数是α_p=0.8，0.6，0.4…。计算结果与参考文献[1]分析结果一致。

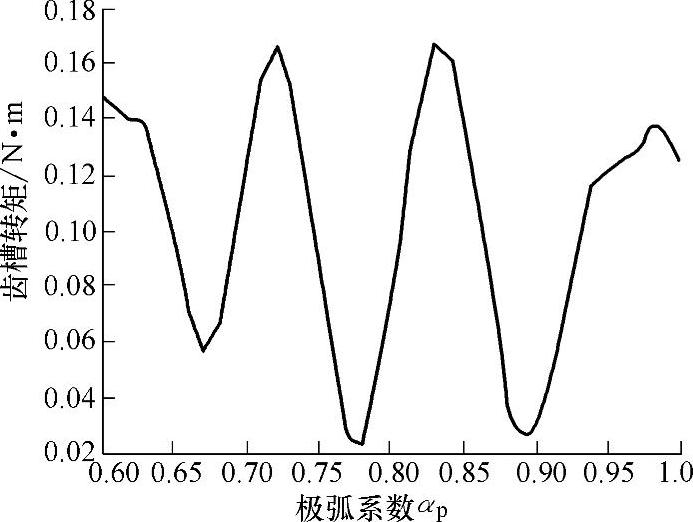
图10-8 9槽8极电机极齿槽转矩与极弧系数α_p关系

参考文献[4]对集中绕组永磁电机齿槽转矩进行理论研究，得到最佳极弧系数和槽口系数：

式中，N₁=0，1，2，…，2p-1；K=1，2，…，Z-1。

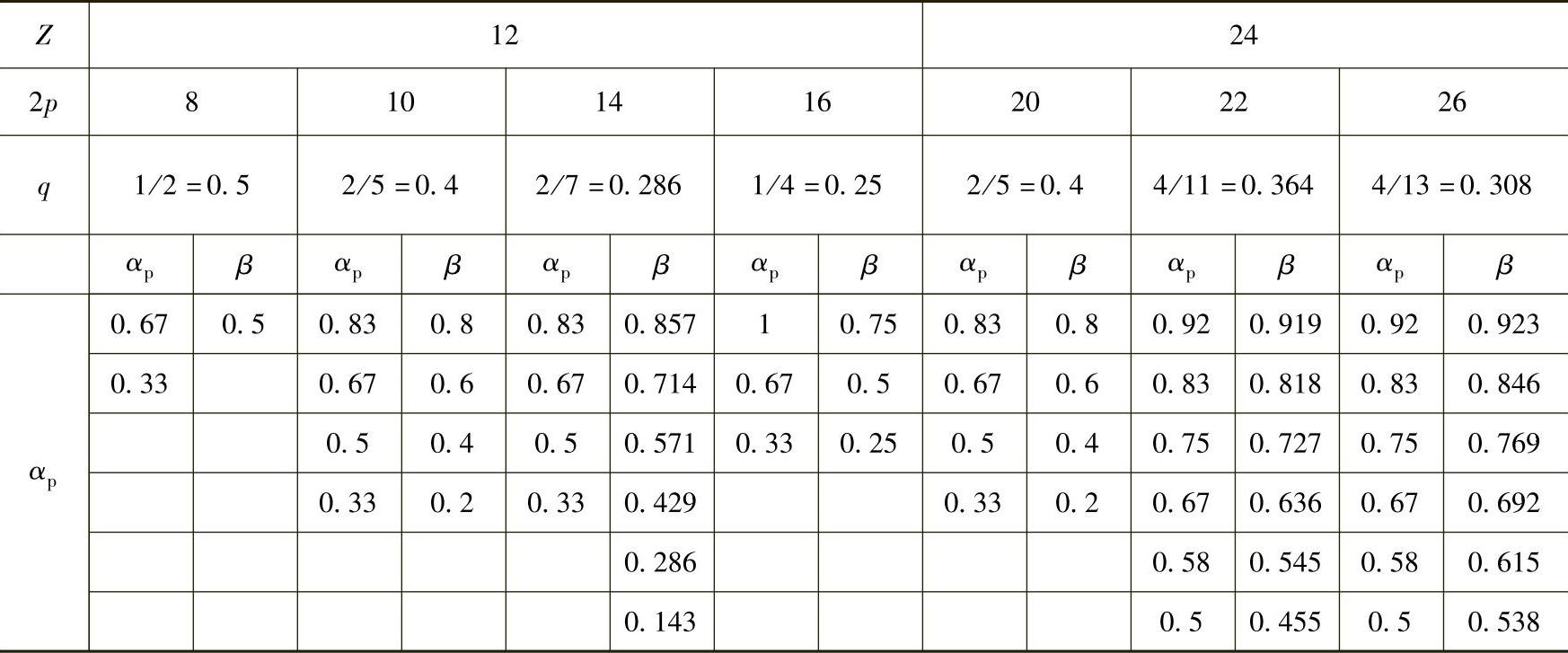
一些12槽和24槽电机最佳极弧系数和槽口系数分析结果见表10-7。表中，在同一个q值下，可以有若干个最佳极弧系数供选择。

为了验证上述分析，用有限元法计算了一台槽口系数为0.08的12槽电机在几种极数下的齿槽转矩峰值与极弧系数关系，结果如图10-9所示。归纳结果如下：

2p=8极时，较好的极弧系数是0.78，相当于表10-7中的0.67加上修正系数为0.17情况；

2p=10极时，较好的极弧系数是0.92、0.76、0.59，相当于表10-7中的0.83、0.67、0.5加上修正系数为0.09情况；

2p=14极时，较好的极弧系数是0.86、0.69、0.53，相当于表10-7中的0.83、0.67、0.5加上修正系数为0.02～0.03情况；

2p=16极时，较好的极弧系数是0.93、0.60，相当于表10-7中的1、0.67减去修正系数为0.07情况。

这些结果说明，表10-7的分析数据和有限元法分析结果接近，有一定参考价值。对于槽口系数为0.08的12槽电机，如图10-9所示，在较好的极弧系数点，2p=10，14有更低的齿槽转矩，而且2p=14最好；2p=8（q=1/2）齿槽转矩明显增高，2p=16（q=1/4）最差。

表10-7 12槽和24槽电机的最佳极弧系数α_p和槽口系数β

以上是对于表面安装磁瓦情况的分析结果。对于内嵌永磁的情况，参考文献[6]对Z/2p=6/4，12/4内嵌式永磁进行有限元分析计算，分析了其齿槽转矩峰值与极弧系数关系，分析的结果如图10-10所示，在q=1/2和q=1两种情况下较好的极弧系数都是取0.68左右。值得注意的是，q=1/2的齿槽转矩峰值约为q=1情况下的一半。

上述的最佳极弧系数是理论分析计算结果，可供参考。实际上，最佳极弧系数还和所用永磁材料、磁化情况（如径向磁化或平行磁化）、气隙大小、槽口宽度等因素有关。上面的最佳极弧系数数据是在小槽口情况分析的结果。参见10.9节分析。

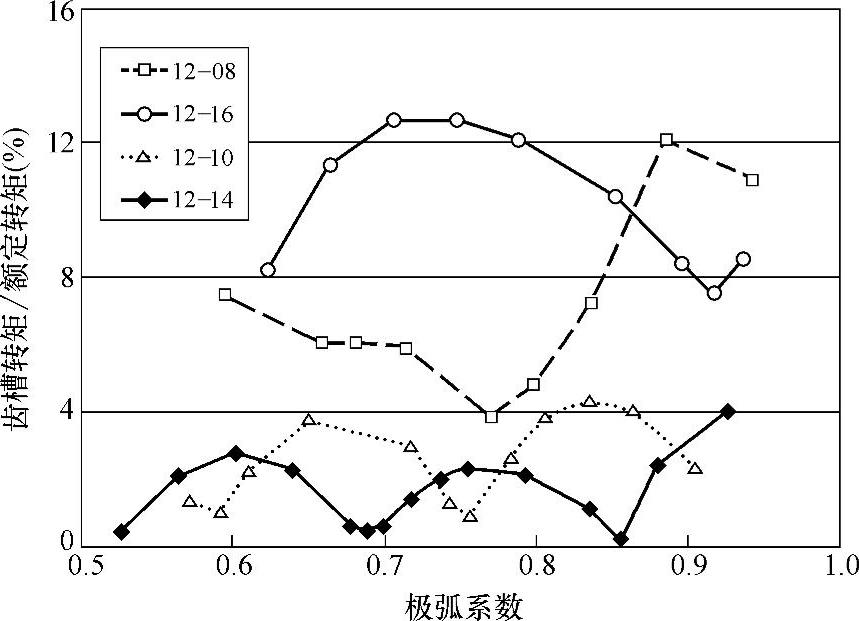
图10-9 12槽电机几种极数下的齿槽转矩峰值与极弧系数关系

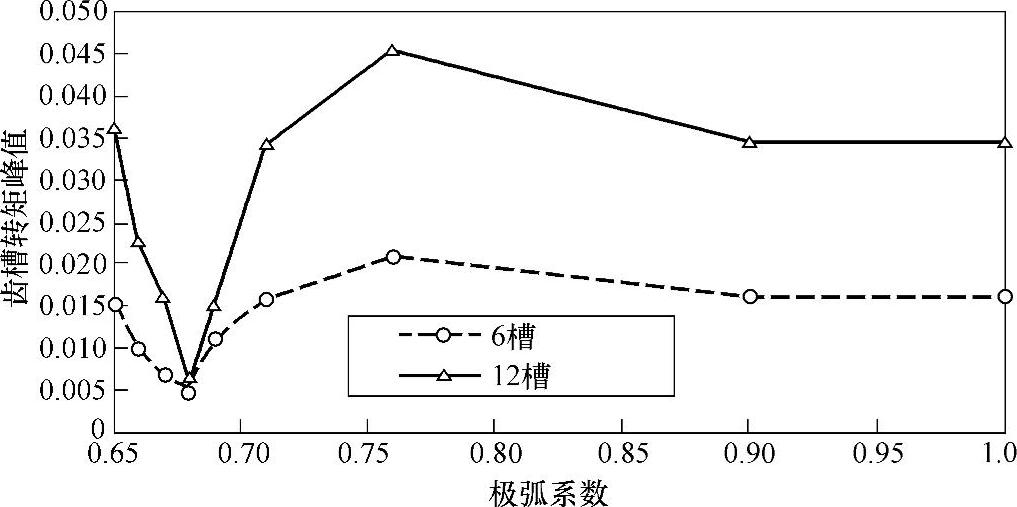
图10-10 6槽和12槽内嵌式永磁4极电机的齿槽转矩峰值与极弧系数关系

需要注意的是，负载时的纹波转矩也随极弧系数变化而变化，但最低纹波转矩的极弧系数和最低齿槽转矩的极弧系数并不一致。例如，第5章图5-11给出12/14组合的纹波转矩和齿槽转矩与极弧比关系有限元分析结果，最低齿槽转矩的极弧系数是0.52、0.69、0.86，而最低纹波转矩的极弧系数是0.91。电机设计时宜兼顾考虑。