首先，考虑槽数Z和极数2p组合与齿槽转矩的关系。通常认为，基波齿槽转矩周期数γ越大，其幅值就越小。所以，宜选择最小公倍数（LCM）较大的定子槽数Z和转子极数2p组合。

Z.Q.Zhu和D.Howe^[2]提出选择定子槽数Z和极数2p组合的评价因子C_T：

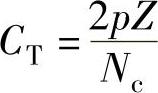
并认为评价因子C_T越小，齿槽转矩的峰值T_c越低。显然，C_T数值上就是槽数Z和极数2p的最大公约数N_m。

由每极每相槽数q的定义，有Z/2p=mq，m为相数，这里m=3，可分别得到三相无刷电动机整数槽绕组和分数槽绕组的评价因子表达式：

1）对于整数槽绕组电机，q为整数，mq必为整数，随之，Z和2p的最小公倍数N_c=Z，最大公约数N_m=2p，N_p=2p/N_m=1。这样，整数槽绕组电机的评价因子表达式为

C_T=2p

2）对于分数槽绕组电机，q为分数，设q=c/d不可约分，有Z/2p=Z₀/2p₀=mc/d，式中Z₀和2p₀是对应单元电机的定子槽数和转子极数。由第5章分析，分数槽绕组单元电机槽数和极数组合的约束条件之一是其极数不允许选择为相数m的倍数，所以d不会等于m或是m的倍数。即mc/d仍为不可约分数。设Z和2p的最大公约数为N_m，有Z=N_m×mc和2p=N_m×d，得最大公约数N_m=2p/d。随之，分数槽绕组的Z和2p的最小公倍数表达式为

N_c=2pZ/N_m=dZ （10-3）

并得到 N_p=2p/N_m=d （10-4）

这样，分数槽绕组电机的评价因子表达式为

C_T=2p/d

上述分析归纳于表10-1。从表可见，有相同槽数Z的分数槽绕组电机与整数槽绕组电机相比，基波齿槽转矩周期数增大d倍；有相同极数2p的分数槽绕组电机与整数槽绕组电机相比，齿槽转矩的评价因子C_T降低了d倍。这个分析清楚说明采用分数槽绕组电机有利于降低齿槽转矩。

表10-1 整数槽绕组与分数槽绕组电机的基波齿槽转矩周期数N_c及评价因子C_T对比

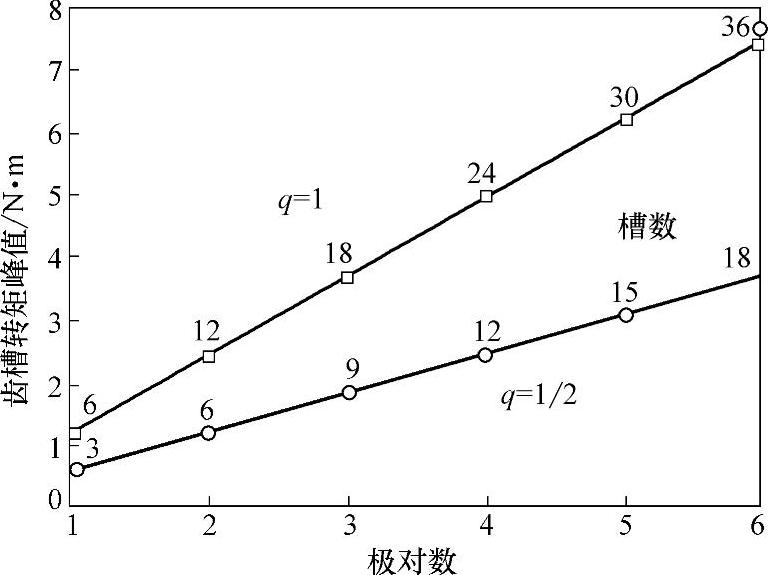
图10-3 q=1和q=1/2几种槽数和极数组合的齿槽转矩峰值的比较

图10-3给出一台电机采用整数槽绕组q=1和采用分数槽绕组q=1/2情况下，几种槽数和极数组合的齿槽转矩峰值的有限元分析结果^[2]。图中，上面一条线表示q=1，槽数分别为6，12，…，36情况，下面一条线表示q=1/2，槽数分别为3，6，…，18情况。从图可见，同一个极对数下，q=1的齿槽转矩峰值约为q=1/2的2倍。其实，这一点从槽口—极间单元模型就很好理解：以最简单的p=1为例，当电动机的转子一个极间面对定子的一个槽口时（此时产生齿槽转矩），在q=1/2情况（Z=3），另一个极间面对定子的齿中央（不产生明显的齿槽转矩），而在q=1情况（Z=6），另一个极间则面对另一个定子的槽口，产生齿槽转矩，使叠加的总齿槽转矩接近2倍。

采用分数槽绕组电机有利于降低齿槽转矩原理在于：它的定子各个槽口所处磁场位置不同，所以各自产生的齿槽转矩相位便不相同，从而，叠加的结果不但提高了基波齿槽转矩周期数，并有可能产生相互抵偿的作用。而整数槽绕组电机每个磁极下的齿槽个数和位置都是相同的，它们在所有极下产生的齿槽转矩相位相同，2p个极的齿槽转矩叠加起来使总齿槽转矩大为增加。(www.daowen.com)

在表10-2和表10-3分别给出Z为奇数和Z为偶数的三相分数槽集中绕组单元电机与q=1整数槽绕组的齿槽转矩基波周期数N_c和评价因子C_T比较。从表可见，和整数槽电机相比，在同样极数下，分数槽集中绕组电机以较少的槽数得到小的评价因子C_T和较大的齿槽转矩基波周期数N_c值。

从表10-2和表10-3可见，引入评价因子C_T概念只能显示分数槽电机优于整数槽电机，而在评价不同Z/2p组合的分数槽绕组电机方面作用不大：Z₀为奇数分数槽单元电机的基波齿槽转矩周期数N_c=2p₀Z₀，评价因子C_T都等于1；Z₀为偶数集中绕组单元电机的基波齿槽转矩周期数N_c=p₀Z₀，评价因子C_T都等于2。这里Z₀和p₀分别是分数槽集中绕组单元电机的槽数和极对数。

所以，评价不同的分数槽集中绕组电机的齿槽转矩时，我们不如关注它们槽极数组合的最小公倍数N_c或N_p。在表10-2和表10-3所列的分数槽集中绕组中，q=1/2、1/4的组合，它们的N_c值较低。随着极数增加（2p≥8），可选择的Z/2p组合有较高的最小公倍数N_c值，这意味着它们会有较低的齿槽转矩。这里说的集中绕组是指线圈元件的节距y=1，即一个线圈元件绕在一个齿上。分数槽集中绕组选择合适的槽极数组合，定子铁心无须斜槽情况下，可能获得满意的低齿槽转矩效果，而且便于定子绕组的自动绕线，工艺上更为简便，所以分数槽集中绕组获得越来越广泛采用。在第5章5.3.3节表5-11给出的三相分数槽集中绕组无刷直流电动机Z/2p组合的LCM值，可利用该表对拟选择的Z/2p组合的齿槽转矩强弱作初步评估。该表中同一Z列的Z/2p组合，宜取q=1/3～1/4的组合，一般会有较大的LCM值。

表10-2 Z为奇数集中绕组单元电机与整数槽电机的齿槽转矩周期数N_c和评价因子C_T比较

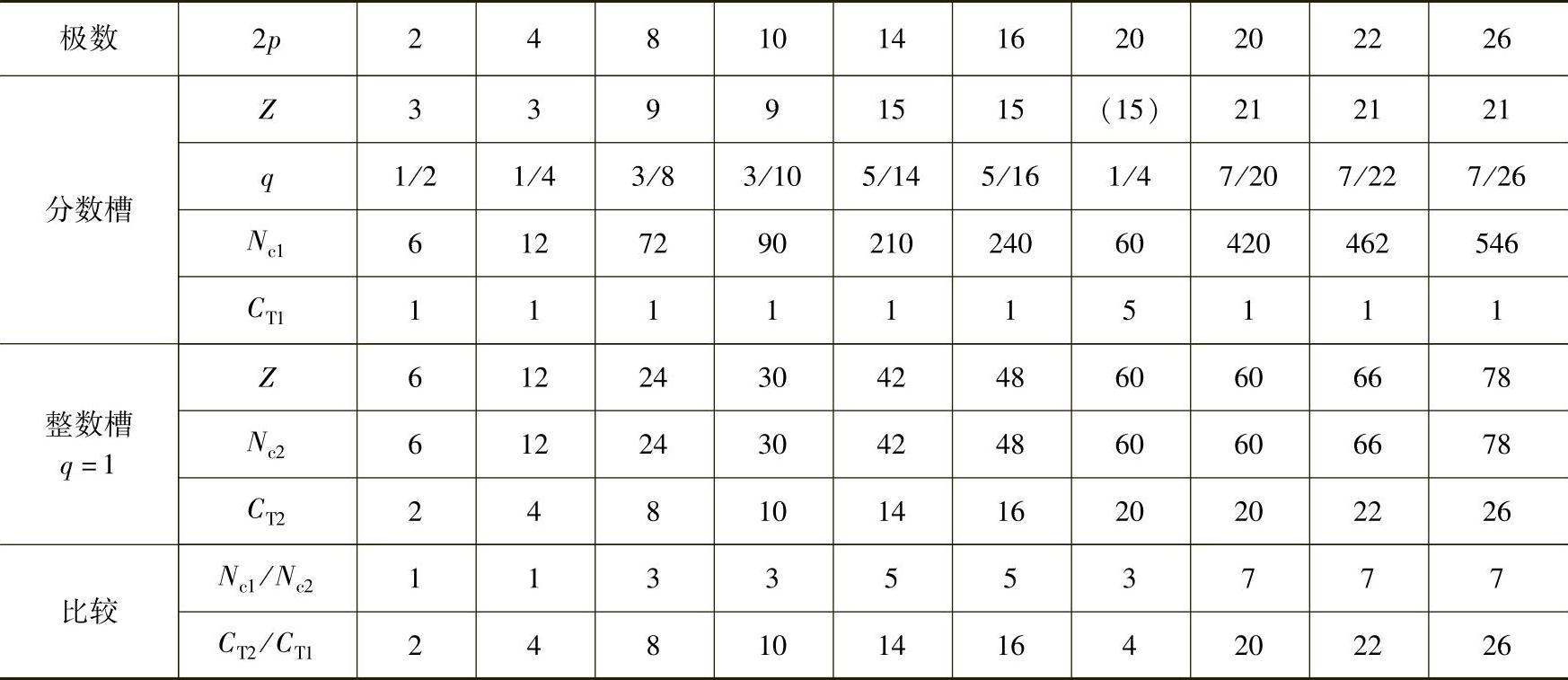
注：有括号的不是单元电机。

表10-3 Z为偶数集中绕组单元电机与整数槽电机的齿槽转矩周期数N_c和评价因子C_T比较

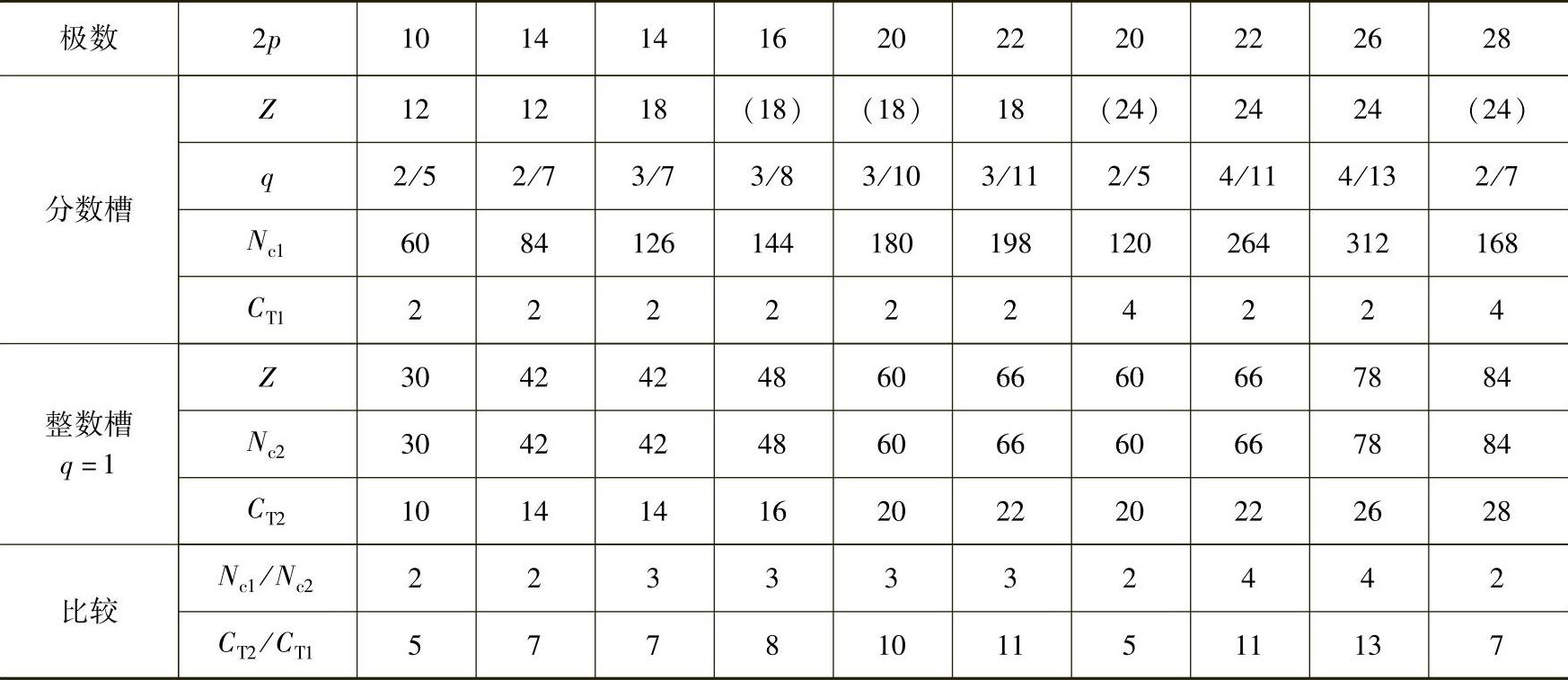
注：有括号的不是单元电机。

这里给出一台具体电机数据，显示按三个不同q值设计下的齿槽转矩有限元分析结果。该电机是外转子结构，磁片表面粘结，电机主要数据见表10-4。在图10-4给出它们的齿槽转矩有限元分析结果：q=1整数槽电机齿槽转矩最大，约为q=0.5电机的8倍。两个分数槽电机小了许多，其中，q=0.36的齿槽转矩几乎为零。由磁片弧度角，可计算得到极弧系数是0.67。按10.4节分析，对于这三个q值电机都是最佳极弧系数。并且它们有相同的槽口宽度。两个分数槽电机B和C齿槽转矩之所以如此大差异，它们的最小公倍数（LCM）值有明显差距是主要因素^[13]。

在图10-5给出9槽6极与9槽8极两台电机齿槽转矩的比较，它们有相同的定子冲片，仅转子极数不同。尽管它们都是分数槽集中绕组，但齿槽转矩有很大差异，因为它们的最小公倍数（LCM）一个是18，而另一个是72。

表10-4 电机主要数据

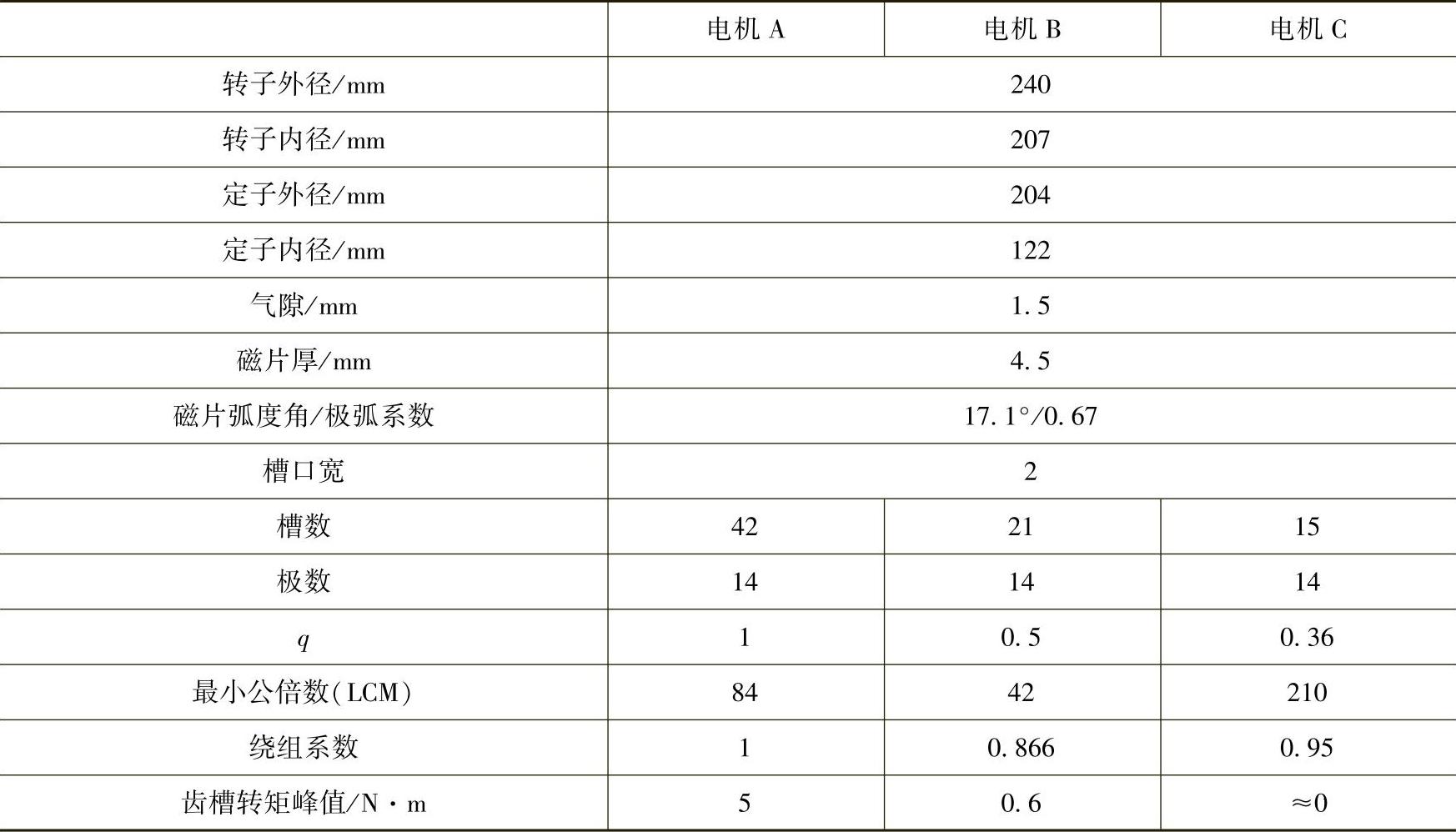
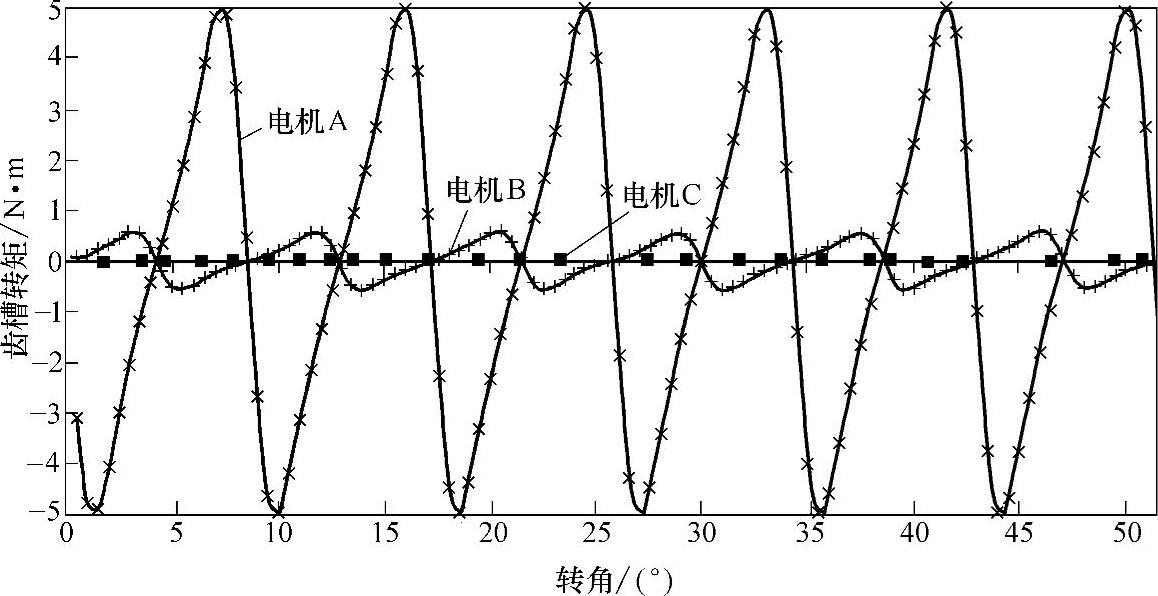
图10-4 三个电机齿槽转矩比较

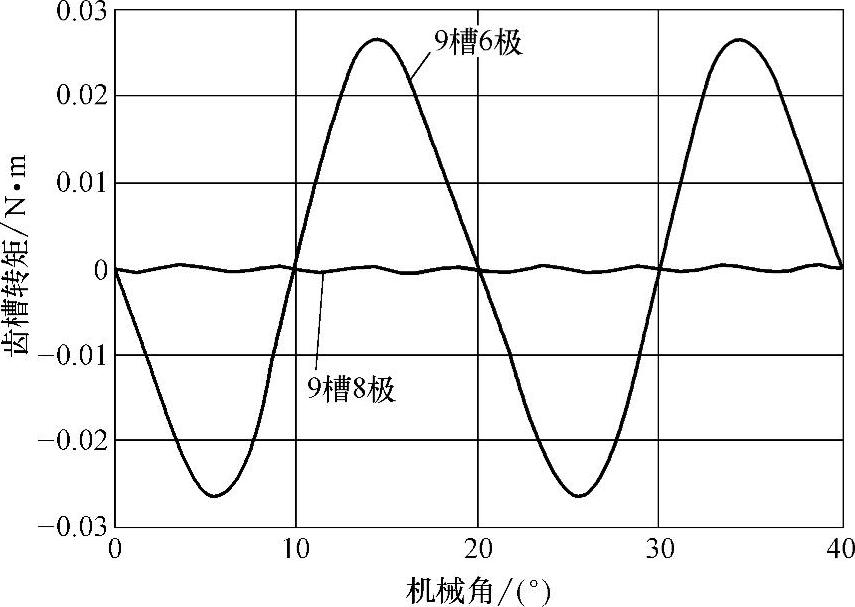
图10-5 9槽6极与9槽8极电机齿槽转矩的比较