对于永磁电机来说，储存在磁场中的磁共能W为

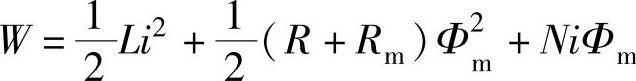
式中，L为定子绕组自感；i为定子绕组相电流；N为定子绕组匝数；R_m为闭合磁路定子铁心的磁阻；R为气隙磁阻；Φ_m为永磁磁通。

在电流i为常数时，由磁共能产生的转矩按下式计算：

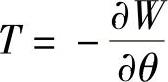
得

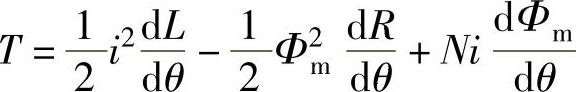
式中的第一项由绕组自感随位置变化引起的转矩；第三项是转子永磁体与定子磁动势相互作用产生电机的有效转矩；第二项为齿槽转矩T_c。齿槽转矩是气隙磁阻变化引起的磁阻转矩，以下式表示：

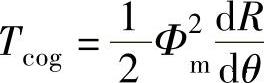
上式表明，齿槽转矩与永磁磁通的平方成正比关系。可见，如果适当降低磁通密度，可以降低齿槽转矩，但是同时也降低了电机的性能。因此，减小dR/dθ是抑制齿槽转矩的可行办法。

在表贴式无刷电机，假设电枢铁心磁导率无穷大，不通电时，电机内存储的磁能可近似表示为永磁体的和气隙中的磁能之和，即

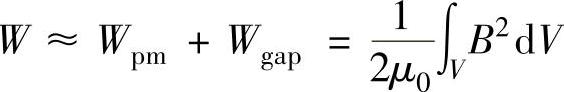
气隙磁通密度沿电枢表面的分布可表示为

B（θ，α）=B_r（θ）G（θ，α）

式中，B_r（θ）是永磁剩磁磁通密度分布；α为某一指定电枢齿中心线与某一指定永磁体中心线之间的夹角。则齿槽转矩可表示为

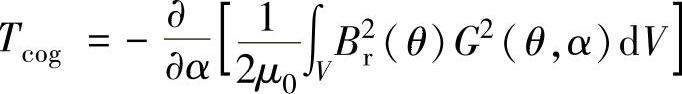(www.daowen.com)

式中，θ为位置角。将B_r（θ）与G（θ，α）分别用傅立叶级数展开，可得齿槽转矩的解析表达式：

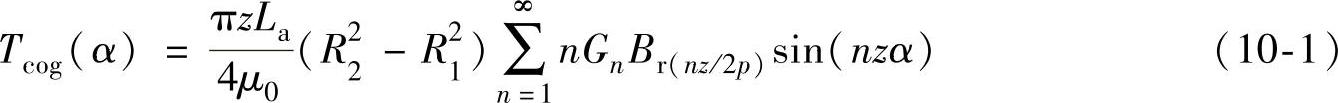
式中，z为槽数；2p为极数；L_a为铁心长度；对于外转子结构，R₁和R₂分别为定子外半径和转子轭内半径；对于内转子结构，R₁和R₂分别为转子轭外半径和定子内半径；n为使nz/2p为整数的整数。

可以利用式（10-1）研究降低齿槽转矩各种方法。由上式可以看出，只有B_r（θ）的nz/2p次谐波分量才对齿槽转矩产生作用，其他谐波分量对齿槽转矩没有影响。因此，设法减小nz/2p次谐波的幅值，可削弱齿槽转矩。

分析表明，永磁直流无刷电动机转子每一转出现的基波齿槽转矩周期数γ与定子槽数Z和转子极数2p的最大公约数（HCF）N_m有如下关系：

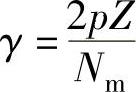
以N_c表示槽数Z和极数2p的最小公倍数（LCM），由于最大公约数N_m与最小公倍数N_c有如下关系：2pZ=N_mN_c，因此得到基波齿槽转矩周期数γ与槽数Z和极数2p的最小公倍数N_c的关系：

γ=N_c=LCM[Z，2p]即转子转过一圈出现齿槽转矩的基波周期数等于定子槽数Z和极数2p的最小公倍数（LCM）N_c。这样，总的齿槽转矩T_c一般可表达为如下形式，它是转子转角θ的函数，由许多谐波组成：

T_cog=∑Tk sin（kN_cθ+θ_k）

实际上，上式可由式（10-1）变换得到。式（10-1）中，要求n为使nz/2p为整数的整数。当取nz=kN_c时，有nz/2p=kN_c/2p=整数，因为N_c是Z和2p的最小公倍数，所以N_c/2p必然是整数。以kN_c代入式（10-1）的nz，即可得到上式。

以N_p表示平均到一个槽距的基波齿槽转矩周期数，

有 N_p=γ/Z=N_c/Z=2p/N_m（10-2）

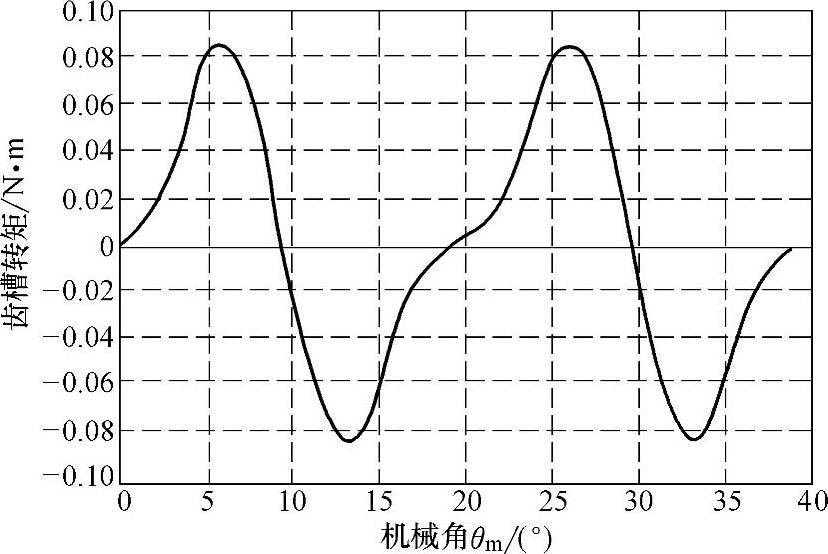
图10-2 齿槽转矩典型波形图

在图10-2给出齿槽转矩典型波形图，它是对一台Z=9，2p=6，q=1/2的分数槽绕组电机有限元分析计算得到的结果。按式（10-1）计算，它的齿槽转矩基波周期数N_c=18，所以其周期为20°。从图可见，每个槽距角40°内齿槽转矩有N_p=2次变化；齿槽转矩波形由许多谐波组成，其中2次谐波比较强。