对于表贴式SMPM电动机，假设气隙磁通密度分布为一个矩形，其宽度与永磁体宽度相同（用电角度2α表示），其最大值为B_m。假设磁铁是径向磁化，磁铁产生的气隙磁通密度幅值B_m由下式计算：

显然，上式是对应于式（6-1）在Cϕ和K_r等于1的情况。

式中，B_r为磁体的剩余磁通密度；μ_r为磁体的相对回复磁导率；δ_e为等效气隙长度；h_m为磁钢厚度；K_leak为两个磁极间的漏磁系数，即式（6-1）中的K₁。使用卡特系数K_c考虑定子开槽效应的影响，等效气隙长度由下式给出：

δ_e=K_cδ式中，K_c为卡特系数，可按下式计算^[6]：

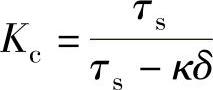
对于开口槽

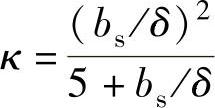
对于半开口槽

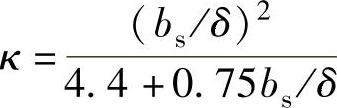
式中，τ_s为定子槽距；b_s为定子槽口宽。

图6-13显示了某多极电机的气隙磁通密度以有限元分析（FEA）法和按式（6-2）计算结果的比较。图中显示了不考虑漏磁（K_leak=1）和考虑漏磁（K_leak≠1）时公式的计算，以及有限元分析（FEA）法计算得到的基波磁通密度B_δ的结果。可以看到，考虑漏磁的公式计算结果与有限元法计算结果基本吻合。

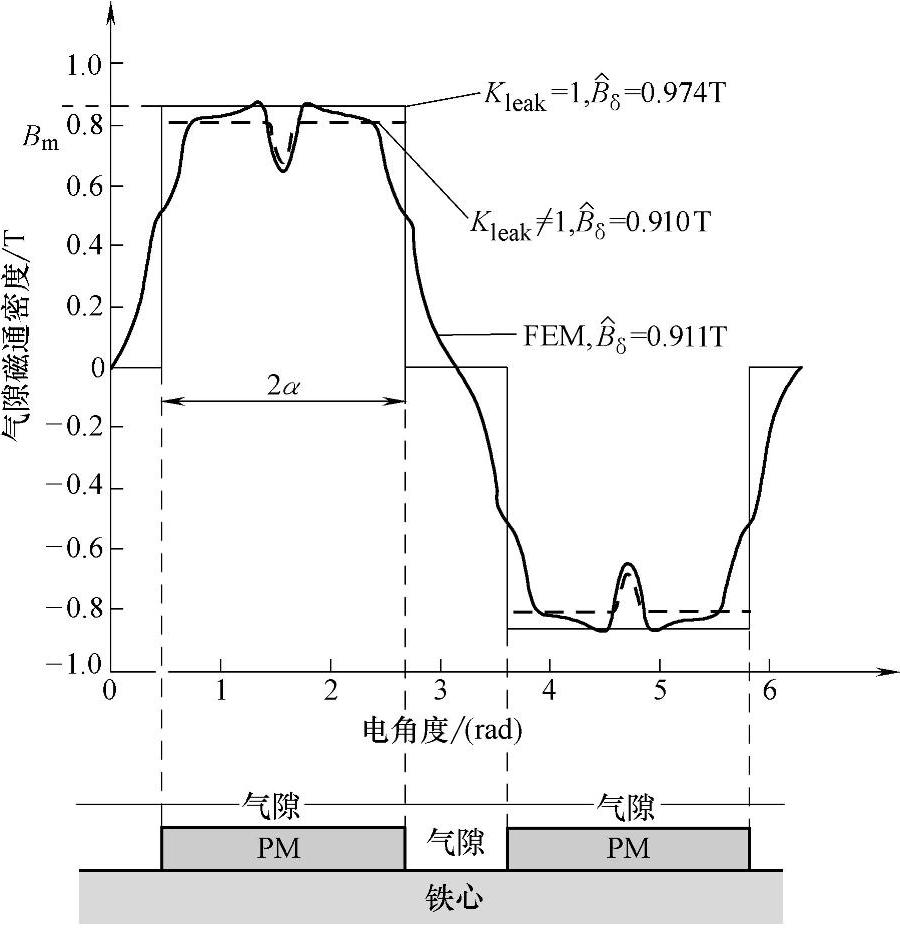
图6-13 一个多极SMPM电动机近似计算和用有限元分析法计算的气隙磁通密度

事实上，假设磁通密度分布为矩形，按上式计算，如忽视漏磁，与有限元分析结果比较，偏离大约在10%以内。有些有限元静态模拟可用来确定系数K_leak与磁极数的函数关系。电机的极数越多，磁体之间的距离越近，漏磁阻将降低，使K_leak增大。磁体之间的漏磁还与磁体高度和气隙长度有关。(www.daowen.com)

漏磁系数可按下式计算：

对于SMPM电机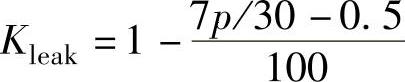

对于外转子式SMPM电机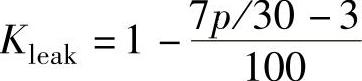

式中，p是电机的极对数。

假设气隙磁通密度分布是一个矩形分布，如图6-14所示。这样，基波气隙磁通密度幅值按下式计算：

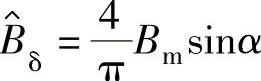
式中，α是磁极角的一半（电角度）。极弧角（2α）通常是选择接近2π/3（120°电角度）。如果增加极弧角到180°，由上式可以使基波气隙磁通密度提高14%，但磁体用量将增加约50%，磁体成本增加了相同的百分数。

利用式（6-2）可估算增加磁体厚度对B_m的作用：选某牌号钕铁硼材料，其μ_r=1.05，B_r=1.15T，分别取电机的h_m/δ=3～5，可计算得B_m=0.85～0.95T。磁体厚度增加约67%，但B_m增大不足12%，所以采用增加永磁体磁化方向厚度的办法来提高B_δ值，其效果是有限的。

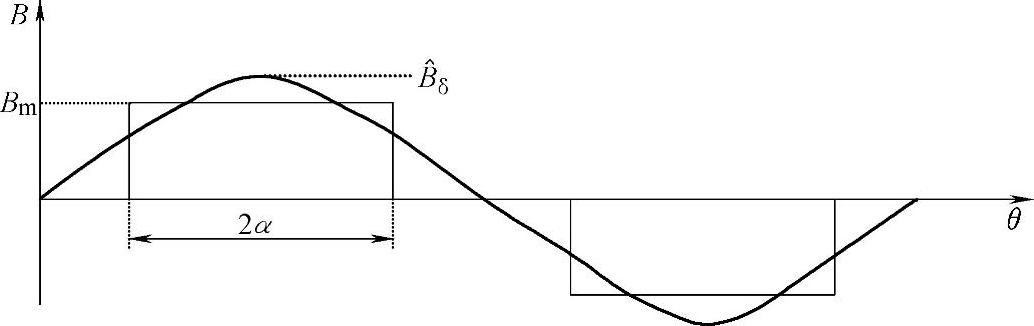
图6-14 气隙磁通密度幅值和基波

表6-5给出对某一5kW低速电机在不同极数设计时气隙磁通密度基波幅值解析计算结果和有限元分析法计算结果的比较，以及它们间的相对误差，可供参考^[4]。解析计算和用有限元分析法计算之间的差别不超过2%。这说明上述解析计算公式可用于工程计算。

表6-5 不同极数的基波气隙磁通密度幅值的解析计算和有限元分析法计算结果比较