1.绕组短距系数计算
如上所述,五相分数槽集中绕组槽数极数应符合Z0=2p0±N,绕组的短距系数kp与补角β相关,kp=cosβ/2。这里,N=βZ0/180°,绕组的短距系数可由下式计算:
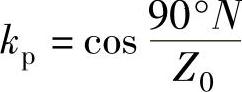
由上式可见,为了获得较大的短距系数,宜取较多槽数,取较小的N。对于同一个槽数Z0,它的基本单元电机(即当Z0为奇数,取N=1;当Z0为偶数,取N=2),可获得较大的短距系数。
2.绕组分布系数计算
分数槽集中绕组电机的绕组分布系数可借助于齿电动势星形图进行分析。下面就定子槽数Z0分别为偶数和奇数的两种情况进行讨论。这里为了得到较大的分布系数,我们只讨论相带数为10的情况。
讨论1,Z0为偶数情况
先看一个例子,图5-20是Z0=20,2p0=22的分数槽集中绕组单元电机齿电动势星形图。本例q=2/11,槽距角α=360°p0/Z0=198°。图中以1,2,3,4…标为齿号,即线圈号排出各齿电动势相量序号,它符合槽距角α=198°的要求。
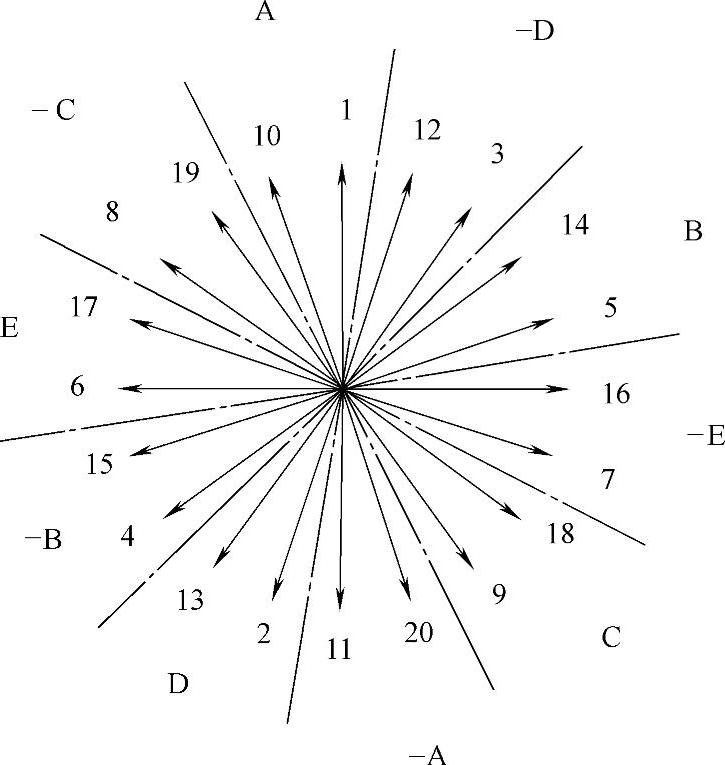
图5-20 Z0/2p0=20/22分数槽集中 绕组单元电机齿电动势星形图
对于分数槽单元电机,此相量星形图是p0个相平面重叠在一起的结果。在本例,20个齿电动势相量分布在p0=11个相平面上。由q=2/11,在11对极下每相平均有4个齿电动势相量。
这里引入虚拟电机概念,即将此多极单元电机齿电动势相量星形图看成是一对极的虚拟电机的齿电动势星形图。虚拟电机的定子槽数仍为Z0,但极对数为1,全部齿电动势相量在一个相平面上。(www.daowen.com)
一般而论,对于五相集中绕组电机,当Z0为偶数时,Z0必然是10的倍数,有q=c/d=(Z0/10)/p0,c=Z0/10,d=p0;它的虚拟电机q′=qp0=c是一个整数。所以,当Z0为偶数时,它对应的一对极的虚拟电机是一个整数槽电机,它们的齿电动势星形图相同。虚拟电机定子槽数仍为Z0。这样,Z0为偶数的五相集中绕组电机绕组分布系数的计算变为此虚拟电机的一个整数槽绕组分布系数的计算:
由整数槽分布系数公式,代入Z=Z0,q=Z0/10,α=360°/Z0
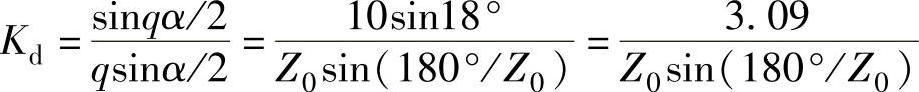
讨论2,Z0为奇数情况
先看一个例子,图5-19a是m=5,Z0=25,2p0=24单元电机的齿电动势星形图,它是Z0为奇数的例子。本例的q=5/24,槽距角α=172.8°。
对于单元电机,此相量星形图是p0个相平面重叠在一起的结果。在本例,25个齿电动势相量分布在p0=12个相平面上。由q=5/24,在12对极下每相平均有5个槽电动势相量。
这里也将此12对极单元电机齿电动势相量星形图看成是一对极的虚拟电机的相量图。虚拟电机定子槽数仍为Z0=25,但极对数为1。全部齿电动势相量在一个相平面上。两个相邻相量之间的夹角α′=360/25=14.4°,q′=25/10=5/2。显然,此虚拟电机仍然是一个分数槽电机。它表示平均每相在每个极下的线圈数还不是整数,但平均每相在每对极下线圈数已是整数。为此,我们将这个虚拟电机的槽数取两倍,即Z=2Z0,构成一个新虚拟电机。这个新虚拟电机的q″=5,这样,平均每相在每个极下的线圈数就是整数了。
一般而论,当Z0为奇数时,Z0必然是5的倍数,但不是10的倍数,有q=c/d=(Z0/5)/2p0,必然有:c=Z0/5,d=2p0,它的虚拟电机q′=qp0=c/2不是一个整数,但乘以2就是一个整数。所以,当Z0为奇数时,它的新虚拟电机槽数Z取原多极单元电机的2倍,即Z=2Z0。这样,Z0为奇数的五相集中绕组电机绕组分布系数的计算变为此新虚拟电机的一个整数槽绕组分布系数的计算:
由整数槽分布系数公式,代入Z=2Z0,q=Z0/5,α=180°/Z0
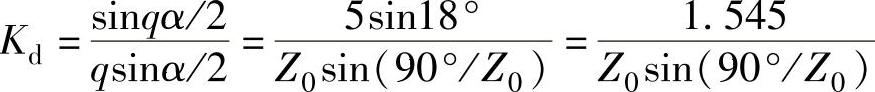
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






