下面，我们借助槽电动势星形图对节距y=1五相分数槽绕组集中绕组槽极数的约束条件进行分析，参见图5-18。图5-18a和b分别表示槽极数比Z₀/2p₀=5/4和5/6槽电动势星形图，是五相电机最简单的槽极数组合例子。图中，相邻两个槽电动势相量之间夹角称为α′，有

α′=360°/Z₀

绕在一个齿上线圈元件的第一元件边电动势相量为1号相量，在+Y轴上，跨过槽距角α为第2元件边电动势相量，即2号相量。这两个相量之间的夹角表示两槽之间的夹角，即槽距角α（电气角，度），有

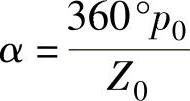
它的补角β，就是2号相量和-Y轴之间夹角。绕组的短距系数k_p与补角β相关，可由下式计算：

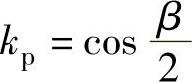
情况1，类似于图5-18a情况：

β=180°_-α=180°-360°p₀/Z₀

得 Z₀-2p₀=βZ₀/180°

情况2，类似于图5-18b情况：

β=α-180°=360°p₀/Z₀-180°

得 2p₀-Z₀=βZ₀/180°

将两种情况归纳为一个表达式：

Z₀=2p₀±βZ₀/180°

再设2β为相邻两个槽电动势相量之间夹角α′角的整数倍，即2β=Nα′，N=1，2，3…

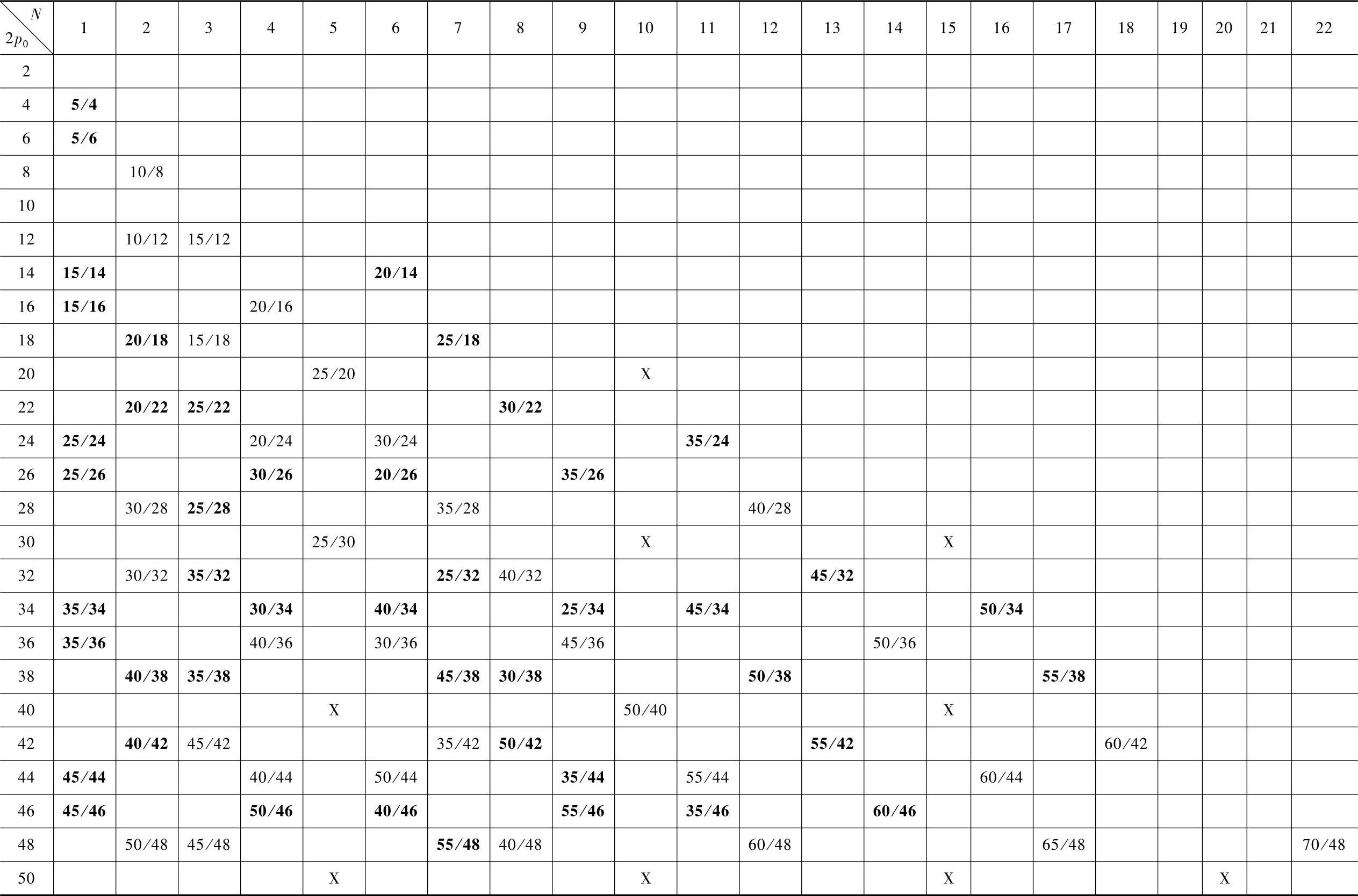
表5-19 五相无刷直流电动机分数槽集中绕组z₀/2p₀组合计算表（条件：Z_O=2p_O±Ⅳ，Z_O≥3Ⅳ）(www.daowen.com)

有2β=360°N/Z₀，即N=βZ₀/180°。

代入上式，得

Z₀=2p₀±N，N=1，2，3…

式中，当Z₀为奇数时，N应取奇数；当Z₀为偶数时，N应取偶数。

上式给出分数槽集中绕组的槽数和极数之间的关系，它与绕组的相数无关，可用于三相绕组也可用于五相绕组。

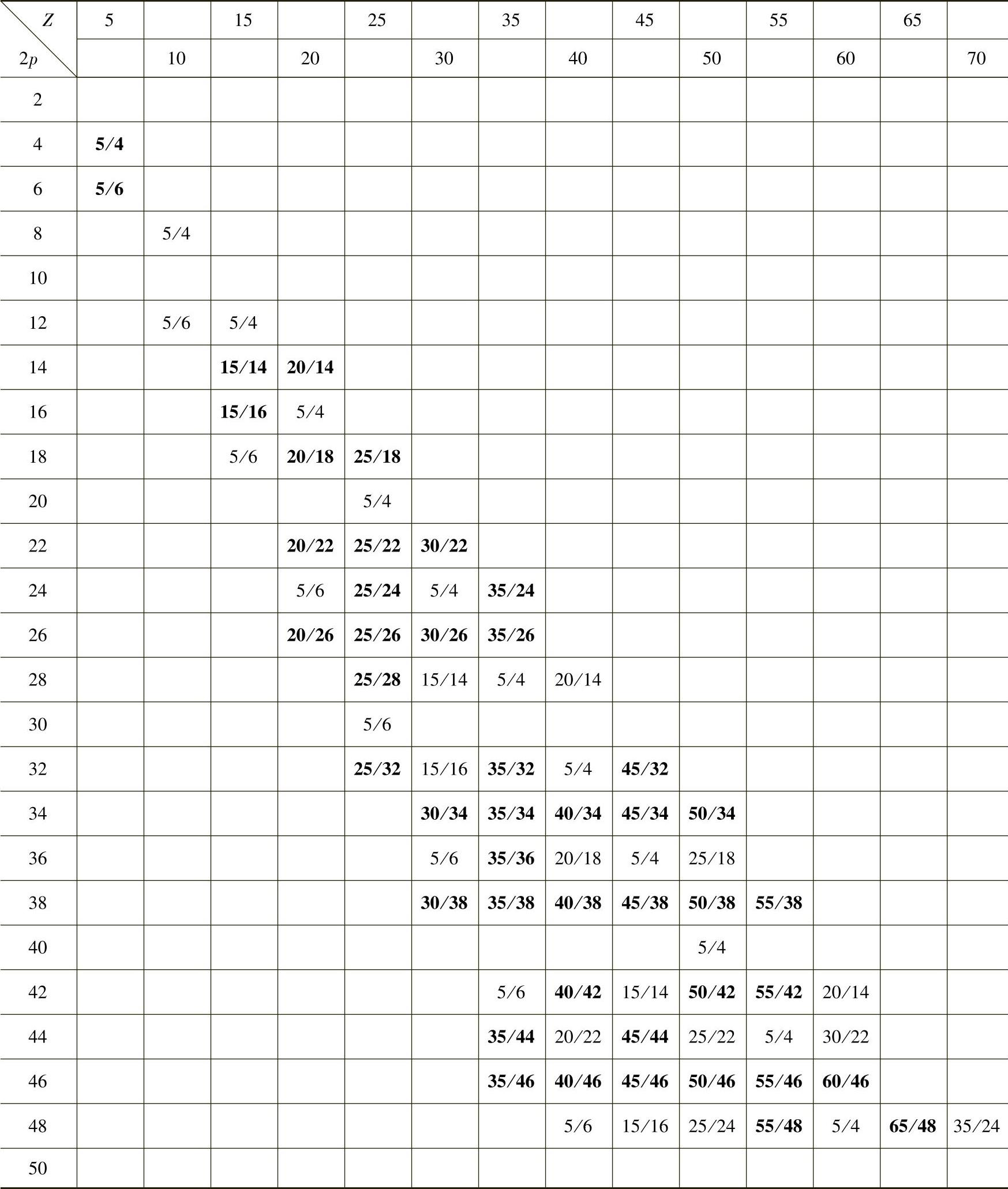
表5-20 五相无刷直流电动机分数槽集中绕组Z/2p组合选择表

符合上式关系的Z₀和p₀可以构成y=1的分数槽集中绕组。利用该公式，可以得到表5-19五相无刷直流电动机分数槽集中绕组Z₀/2p₀组合计算表。在计算表中，每个p₀在不同N值下计算出Z₀/p₀的值。在完成此表时，还需要按照下面条件挑选出正确的组合：

1）Z应为5倍数；

2）β≤60°（要求短距系数k_p≥0.866），由N=βZ₀/180°，即应满足Z≥3N。表中，黑体字的Z₀/p₀组合是单元电机组合；非黑体字的可约分数的组合不是单元电机组合。

由表5-19，重新编排，可得到表5-20五相无刷直流电动机分数槽集中绕组Z/2p组合选择表。凡表中有分数的方格表示了短距系数k_p≥0.866附加条件下可以选择的Z/2p组合，它们可以构成y=1的分数槽集中绕组。表中，黑体字的Z/2p组合是单元电机组合；非黑体字的组合不是单元电机组合，其方格内的分数表示它对应的单元电机的组合。

限于篇幅，表5-20中只给出2p在50以内，Z在70以内的情况，读者参照表5-19分析方法，可以将表5-20扩展到更大的Z和2p的情况。

只有表5-20中有分数的方格所表示的Z/p组合才可能构成y=1的分数槽集中绕组，所以，可供选择的Z/p组合是有限的。设计五相无刷电动机y=1的分数槽绕组电机时，可在表中从填有分数字的方格中选取Z/2p组合。