如上所述，集中绕组单元电机的槽极数组合总是成对出现的，它们有下式所示的关系：

Z₀=2p₀±N

对于相同的N，同一个槽数Z₀的铁心，两种极数2p₀下有相同的绕组系数。设计时对于极数2p₀有两种选择：是取槽数大于极数方案？还是槽数小于极数方案？例如，一台12槽定子电机可选择2p₁=10极和2p₂=14极，取极数少还是极数多好？为此，作如下分析：

1.定子铁损耗比较分析

定子铁损耗指齿部和轭部铁损耗，通常人们乐意取极数较少的方案，因为定子铁心的工作频率较低对减少定子铁损耗有利。工作频率按下式计算：

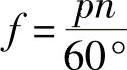
但是，以齿部铁损耗为例分析，铁损耗与磁通密度和工作频率有如下关系：

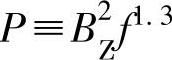
设气隙磁通密度幅值B_m相同，采用同一个定子铁心，分别计算极数少（2p₁）和极数多（2p₂）时的齿部磁通密度：

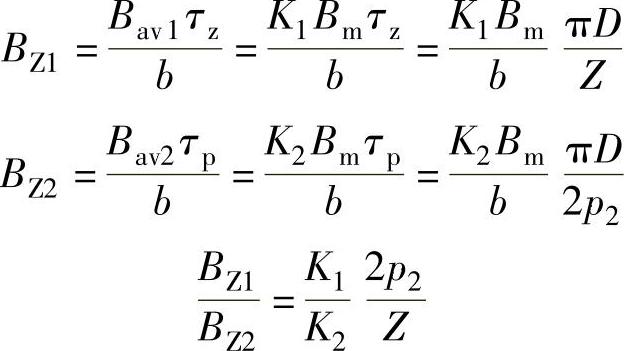
式中，b为齿宽；τ_z为齿距；τ_p为极距；D为气隙直径；B_m为气隙磁通密度幅值；B_av为气隙磁通密度平均值；K₁和K₂分别是两种情况下的气隙磁通密度平均值与气隙磁通密度幅值之比的系数，它们和气隙磁通密度的分布波形有关。

计算例1：槽数Z=12，选择2p₁=10和2p₂=14。图5-12是2p<Z和2p>Z的齿部磁通密度比较示意图，表示此时的齿和磁极相对位置齿部磁通密度最大，在忽略漏磁假定条件下比较齿部磁通密度大小。

图5-12 2p<Z和2p>Z的齿部磁通密度比较示意图

1）设气隙磁通密度分布为120°梯形波，有

在同一转速情况下，齿部铁损耗比：

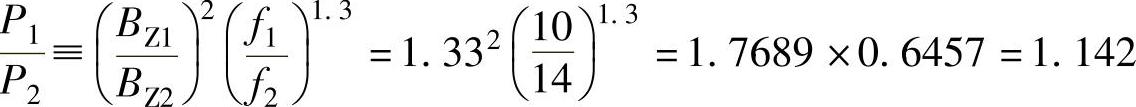(www.daowen.com)

2）设气隙磁通密度分布为90°梯形波，有

上述计算表明，10极比14极的齿部磁通密度大许多，即使10极时工作频率低，但未能够抵偿齿部磁通密度的增加，总齿部铁损耗10极比14极大。

计算例2：槽数Z=9，选择2p₁=8和2p₂=10。

设气隙磁通密度分布为120°梯形波，有

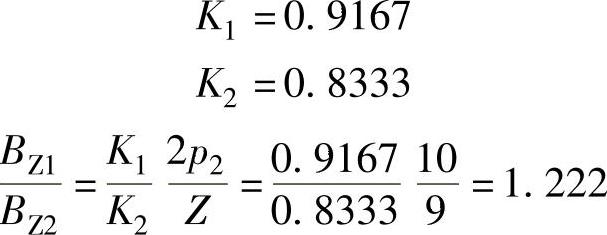
在同一转速情况下，齿部铁损耗比：

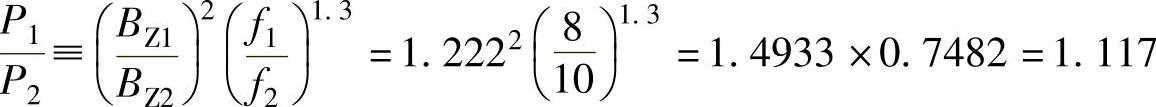
上述计算表明，齿部铁损耗8极比10极大。

看来，采用极数大于齿数有利。

2.齿槽转矩的比较分析

前面提到，在比较齿槽转矩大小时常常按所选择的槽数Z和极数2p的最小公倍数LCM评估。通常有较多极数的比较小极数的有较大的LCM，随之有较小的齿槽转矩。

对于12槽电机，选择2p₁=10极和2p₂=14极的例子，有LCM₁=60；LCM₂=84。

对于9槽电机，选择2p₁=8极和2p₂=10极的例子，有LCM₁=72；LCM₂=90。

此外，如5.3.4节所述，当Z为奇数单元电机时，存在不平衡拉力问题。参考文献[12]分析比较Z/2p=9/8和9/10两种情况的不平衡拉力，10极明显低于8极，振动和噪声较低。

综合上述分析，成对出现的分数槽集中绕组电机槽极数组合宜选择极数大于槽数的组合。