观察表5-8和表5-11发现，与Z为偶数的Z/p组合相比，Z为奇数的Z/p组合更有优势：有较多的选择机会，有较高绕组系数，有较大LCM，即齿槽转矩较小。但是，Z为奇数的Z/p组合不推荐使用，因为它们存在不平衡径向磁拉力（UMP）问题。

表5-13是Z为奇数单元电机双层绕组排列表，注意表中有*的组合，它们是符合Z₀=2p₀±1的基本组合。观察表5-13绕组排列发现，这些有*组合的绕组排列有相同规律：沿着电机气隙圆周360°分为三个区，每相线圈集中到约120°的一个区内。这样，对每一相绕组来说，在气隙圆周上的分布是偏向一边的，不平衡的。

在径向磁场电动机气隙中，电磁效应产生的切向力、径向力和磁致伸缩力都会引起电磁噪音。切向力产生定子和转子之间的有用电磁转矩。而径向力是在定子和转子之间的吸引力，磁致伸缩力在磁场的方向对铁心的拉伸力。径向力是径向磁场永磁电动机电磁噪音的主要来源。在电机运转时，偏置的相绕组产生偏置的定子电枢反应磁场，它和在气隙中永磁转子产生的磁场合成为不平衡的合成磁场，产生不平衡的径向磁应力，称为不平衡径向磁拉力（UMP）。随着电机的换相，这种不平衡径向磁拉力是旋转的，每经过一个电气换相周期（6个状态），不平衡径向磁拉力旋转一周，其频率为电动机转子旋转频率的p倍，引起电机高频振动和噪声。如果转子在机械上还存在偏心，振动和噪声将加剧。

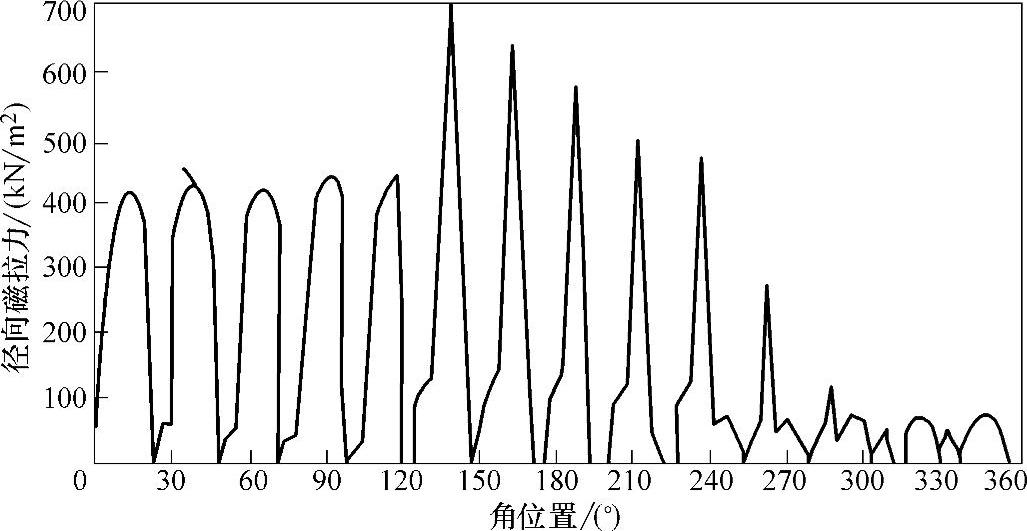
图5-10 Z/2p=15/14的径向磁拉力分布

举例来说，参考文献[8]针对一台Z/2p=15/14电机用有限元法得到电机通电时的径向磁拉力分布图（见图5-10），显示出明显的不平衡的径向磁拉力，会引起定子（和转子）的单向偏移。所以该文认为：不宜选取那些槽数和极数接近而槽数是奇数的组合，如Z/2p=9/8，15/14，21/22等。

为了解决这个问题，可考虑采取如下措施：

1.优化电机设计参数，降低UMP和它的影响

例如，为设计高性能硬盘，解决原先采用的9/8组合的硬盘主轴电动机不平衡磁拉力引起振动和径向跳动已经变得十分迫切。参考文献[11]提出降低UMP引起振动的坚固设计方法。通过优化电机设计参数，使UMP影响减到最少。并注意提高制造质量，降低如槽口制造偏差，和减少由于磁钢磁化工装和磁化过程引起转子磁通密度分布的不平衡。(www.daowen.com)

日本东方马达株式会社在开发小型无刷直流电机时，对比了几种9槽电机方案，指出Z/2p=9/8和9/10方案在绕组系数和齿槽转矩方面有较高性能，但是它们会产生径向不平衡电磁力，可能产生严重的振动和噪声。采用有限元法分析结果，运行时径向不平衡电磁力变化频率是转子旋转频率的p倍，发现在相同电磁转矩条件下9/8电机产生的径向不平衡电磁力比9/10电机产生的径向不平衡电磁力大许多，约4倍。该公司在42mm机座号小型无刷电机新产品中改用了9/10槽极配合方案。并且在电子驱动器采用了正弦波驱动方式，进一步降低电机的振动和噪声^[12]。

2.改为采用Z为偶数的槽极组合

著名硬盘制造商昆腾公司早在1997年就发现，过去它们的硬盘无刷电动机采用的9/8组合存在不平衡径向磁拉力（UMP）问题，影响硬盘机性能的提高。昆腾公司将他们的硬盘无刷电动机方案改换为12/10组合，以提高硬盘机工作的平稳性，并申请了美国专利[13]。

应当指出，上述关于Z为奇数的Z/p组合存在不平衡径向磁拉力（UMP）问题，只是对于单元电机数t=1的组合（即表5-13中带*的组合）才存在。所以，可采取下面两个途径回避不平衡径向磁拉力问题：

（1）选择多个单元电机组合

对于表5-13中带*的Z₀为奇数的单元电机，如果取单元电机数t≥2，对应的Z/p组合并不存在不平衡径向磁拉力（UMP）问题。例如Z/p=18/10组合，它由两个9/5组合单元电机组成，即t=2，参见表5-15，绕组分布没有不平衡问题。这样，可参见表5-3，选择那些单元电机是9/4，9/5，15/7，15/8，21/10，21/11…的组合。这些组合由于其单元电机的Z₀为奇数，具有较高绕组系数，较大LCM，较小齿槽转矩的优点。表5-12给出了这样的例子，第1和第2行有相同槽数，极数也相近，9/4的单元电机是Z₀为奇数的组合，则有较小的齿槽转矩。绕组系数方面，Z₀/p₀=12/5的K_w=0.933，而Z₀/p₀=9/4的K_w=0.945，稍大。

（2）选择非基本组合的其他组合

带*的组合是Z为奇数的Z/p组合中的基本组合，即符合Z₀=2p₀±1的组合，如表5-3所示，对于Z≥21，槽数Z为奇数的每个Z列中，除了两个基本组合外，还有其他的Z/p组合可以选择。虽然它们的绕组系数不如基本组合高，但绕组分布已不存在不平衡径向磁拉力问题。参见表5-13，如21/8，21/13，27/10，27/11，27/16，27/17，33/13，33/14，33/19，33/20…可选取使用。我国电动自行车用无刷直流电机中最常用的51/23槽极数组合属于这样的成功实例。