
研究分数槽绕组时可借助于槽电动势相量星形图进行分析。实质上,一相绕组分布系数的计算是一相绕组所占两个60°相带内槽电动势相量的合成问题。下面我们首先讨论定子槽数Z0分别为偶数和奇数的两个代表性的例子。
【例5-1】Z0为偶数的例子,m=3,Z0=12,p0=5的单元电机
图5-1a是Z0=12,p0=5的单元电机槽电动势相量星形图。本例q=2/5。槽距角α=360p0/Z0,在本例α=150°。图中以1,2,3,4…标为槽号,排出各槽电动势相量序号,它符合槽距角α=150°的要求。同时,在图5-1b给出Z0=12,p0=7,q=2/7的单元电机槽电动势相量星形图。
对于此单元电机,此相量星形图是p0个相平面重叠在一起的结果。在本例,12个槽电动势相量分布在p0=5个相平面上。由q=2/5,在10个极下每相平均有4个槽电动势相量。
这里引入虚拟电机概念,即将此多极单元电机槽电动势相量星形图看成是一对极的虚拟电机的相量图。虚拟电机定子槽数为Z0,但极对数为1。全部槽电动势相量在一个相平面上,参见图5-1c。
这样,图中两个相邻相量之间的夹角为α′,是虚拟电机的槽距角,它的每极每相槽数为q′,有

在本例,有α′=30°,q′=2。
由本例可见,q=2/5的分数槽绕组和q′=2的整数槽虚拟电机有相同的槽电动势相量星形图。
【例5-2】Z0为奇数的例子,m=3,Z0=9,p0=4的单元电机。
图5-2a是本例的槽电动势相量星形图。本例的q=3/8。在本例,槽距角α=160°。
对于单元电机,此相量星形图是p0个相平面重叠在一起的结果。在本例,9个槽电动势相量分布在p0=4个相平面上。由q=3/8,在8个极下每相平均有3个槽电动势相量。
这里也将此8极单元电机槽电动势相量星形图看成是一对极的虚拟电机的相量图。虚拟电机定子槽数为Z0=9,但极对数为1。全部槽电动势相量在一个相平面上。两个相邻相量之间的夹角α′=40°,q′=3/2,见图5-2c。本例,虚拟电机仍然是一个分数槽电机。由本例可见,q=3/8的分数槽绕组和q′=3/2的虚拟电机有相同的槽电动势相量星形图。考虑一个新虚拟电机,它的槽数为2Z0=18,即为偶数,q″=2Z0/6=3。新虚拟电机就是一个整数槽电机。在图5-2b给出Z0=9,p0=5,q=3/10单元电机的槽电动势相量星形图。
下面讨论一般情况。在分数槽集中绕组,q表示为q=c/d的一个真分数,对于三相电机,有q=Z0/6p0,又Z0必须是3的倍数,对照【例5-1】和【例5-2】,进行下面的讨论:
讨论1,当Z0为偶数时,必然有:c=Z0/6,d=p0;得q′=qd=c是一个整数。所以,当Z0为偶数时,它的虚拟电机是一个整数槽电机,如【例5-1】图5-1a,q=2/5,d=5,q′=c=2。在槽电动势相量星形图中,每60°相带有2个槽电动势相量。
讨论2,当Z0为奇数时,必然有:c=Z0/3,d=2p0,得q′=qd/2=c/2还是一个分数,但乘以2就是一个整数。所以,当Z0为奇数时,它的虚拟电机还是一个分数槽电机,如【例5-2】图5-2a,q=3/8,c=3,d=8,q′=c/2=3/2。在槽电动势相量星形图中,平均每60°相带有1.5个槽电动势相量,但每相占有2个60°相带,故共有3个槽电动势相量。使三相对称条件仍然成立。考虑一个新虚拟电机,它的槽数为2Z0,即为偶数,q″=2Z0/6=Z0/3=c。
引入虚拟电机概念后,将多极单元电机看成是一对极的虚拟电机,在计算绕组系数时,按虚拟电机计算即可。从绕组的分布效应角度看,多极分数槽单元电机的分布系数和整数槽电机有如下对应关系:
1)对于Z0为偶数的多极分数槽单元电机,其分布系数相当于Z=Z0,即q=Z0/6的整数槽电机的分布系数。如【例5-1】,q=2/5或q=2/7的分数槽单元电机的分布系数和q=Z0/6=2整数槽电机的相同。注意到,这里q=c。
2)对于Z0为奇数的多极分数槽单元电机,其分布系数相当于Z=2Z0,即q=Z0/3=c整数槽电机的分布系数。如【例5-2】,q=3/8或q=3/10的分数槽单元电机的分布系数和q=Z0/3=3的整数槽电机的相同。注意到,这里也是q=c。
2.分数槽单元电机绕组系数一般公式
从上述分析,注意到,无论Z0为偶数或奇数,分数槽单元电机的分布系数和q=c的整数槽电机的相同。由此可推导分数槽集中绕组分布系数公式。
由整数槽电机的分布系数 
对于60°相带,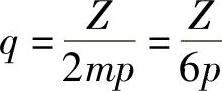 ,
,
槽距角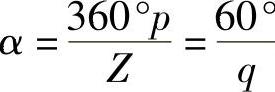 ,
,
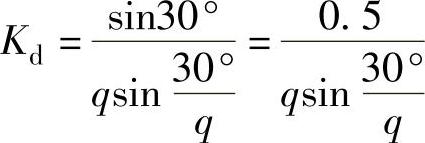
对于分数槽集中绕组,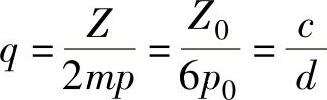 (www.daowen.com)
(www.daowen.com)
其中,c/d是不可约分数。
得分数槽集中绕组分布系数:
由整数槽电机的短距系数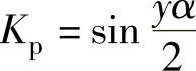
y是线圈节距,对于集中绕组分数槽,y=1,集中绕组分数槽电机的短距系数
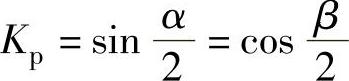
式中,α为槽距角,β为它的补角。
对于分数槽集中绕组,有Z0=2p0±N
式中,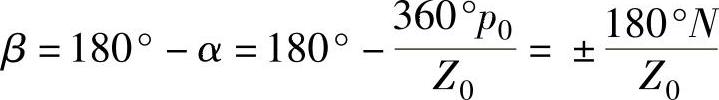
分数槽集中绕组短距系数: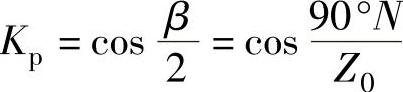
当Z0为偶数时,N为偶数,必然有: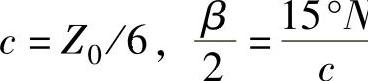 N,
N,

当Z0为奇数时,N为奇数,必然有:c=Z0/3,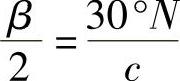

对于基本单元电机,N=1或2,必然有: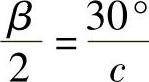 ,
,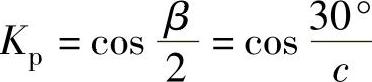
得基本单元电机的绕组系数: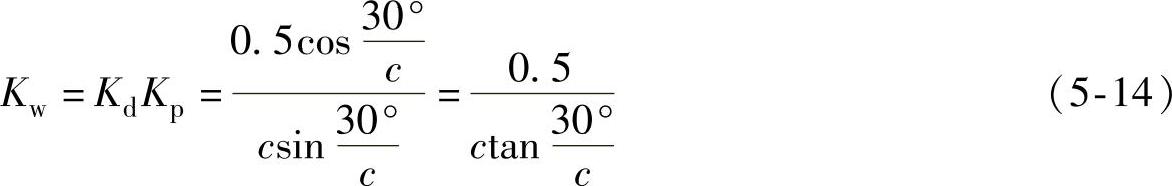
上述分析表明:
1)分数槽集中绕组的绕组系数与q的分子c和N有关,而与q的分母d无关。可利用式(5-12)和式(5-13)进行计算。
2)有相同Z0和N成对的单元电机,虽然极数不同,但c和N相同,所以有相同的绕组系数。例如,Z0/p0=12/5和Z0/p0=12/7是成对的单元电机;Z0/p0=9/4和Z0/p0=9/5是成对的单元电机。
3)基本单元电机的绕组系数只与q的分子c有关。可利用式(5-14)计算。
3.单元电机分布系数计算例
下面给出计算Z0=27,p0=13,q=9/13单元电机分布系数的例子:
由于它是Z0为奇数的多极分数槽单元电机,其分布系数相当于q=Z0/3整数槽电机的分布系数。利用这个关系,计算对应的整数槽电机:q=Z0/3=9,Z=2mq=6×9=54,α=360/54=6.667,利用整数槽绕组分布系数公式(5-10)计算得
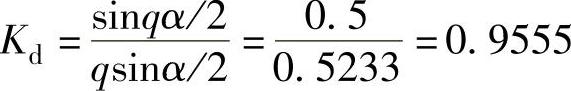
或直接由q=9/13,c=9,利用式(5-12)计算得
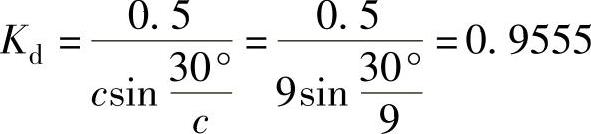
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






