定义转矩系数K_T（N·m/A）等于平均电磁转矩与平均电流之比。当不计电感时，按上述规定的单位制，转矩系数K_T数值上等于反电动势系数K_E。当计及电感时，由式（4-29）

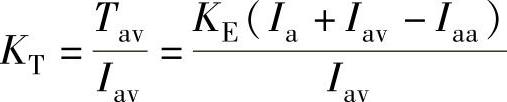
得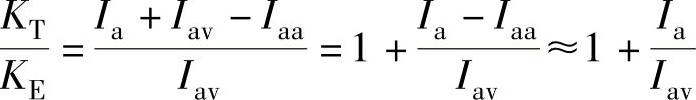

上式显示，由于电感的存在，转矩系数K_T将大于反电动势系数K_E，而且不是常数，随着电流大小而变化。这是续流的A相电流产生附加有效转矩的缘故。从数值上来理解，由于转矩系数等于平均电磁转矩与平均电流之比，如前所述，平均电流等于B相电流平均值，平均电磁转矩却正比于A相和B相电流产生的转矩，所以转矩系数K_T必然比反电动势系数K_E大。

上述过程分析表明，在无刷直流电动机中，参与机电能量转换产生电磁转矩的除了从电源来的电流i_b外。还有一个较小的电磁转矩分量是由电流i_a产生。从能量转换观点看，这个分量是来自电源的能量先前已经转换成磁能存储在绕组电感里，然后在续流过程中一部分的磁储能再参与机电能量的转换，转换成电磁功率，产生电磁转矩。

由式（4-32）和式（4-33）可得到转矩系数与反电动势系数比为

这转矩系数与反电动势系数比是由x和K_u确定，在图4-16给出了它们的函数关系。式（4-36）和图4-16说明：当考虑了电感的存在，转矩系数K_T与反电动势系数K_E并不相等，它们之比也不是一个常数。随着x的降低，此比值逐步增加。从图4-14和图4-15也可以发现，当K_u从1向0.6方向变化时（即转速从高速向中速方向变化），曲线Kτ和曲线K_A分别从曲线K_x向上和向下变化。对于同一个x，随着K_u值的降低，平均电流比在降低而平均电磁转矩比反而在增加，从而使两个系数之比越来越大。从图4-16可见，由于电感的存在，K_T/K_E系数比有如下变化规律：

1）只有在理想空载转速点有K_T=K_E，其余转速下转矩系数K_T都大于反电动势系数K_E。

2）在K_u≥0.6区域，x=0.05时，系数比最大不超过1.5；

3）在K_u≥0.8区域（无刷直流电机额定负载大多数在区域），系数比在1.0～1.2之间；

4）当K_u低于0.6后，K_T与K_E系数比逐渐增大。(www.daowen.com)

5）当x大于5以后，电感影响逐步减小，K_T与K_E系数比逐渐趋近1。

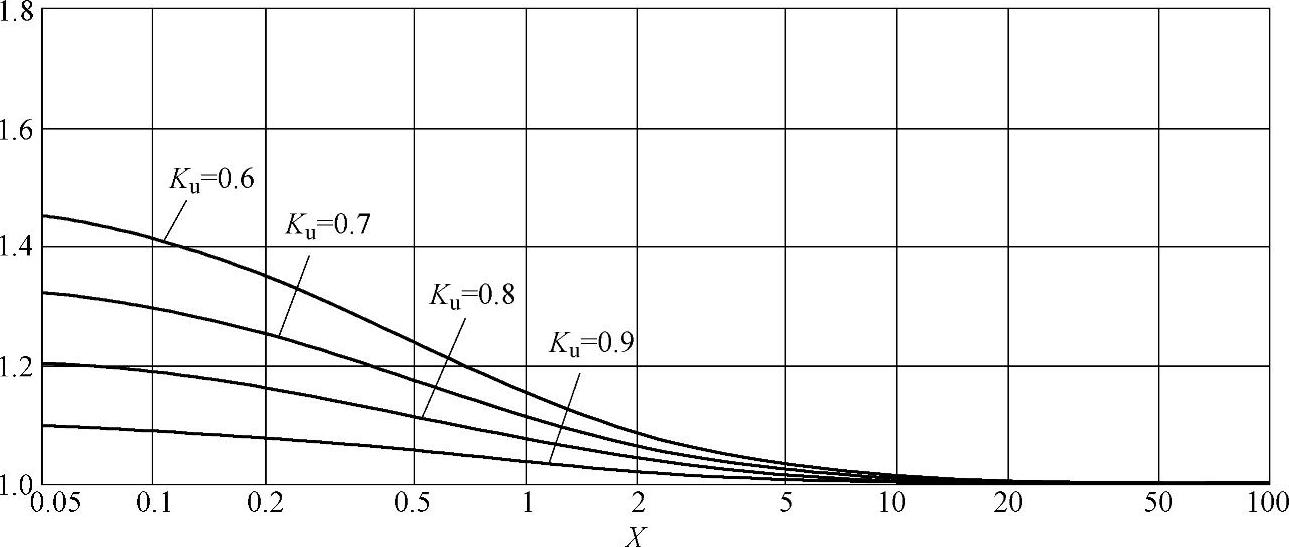
图4-16 K_T/K_E系数比与K_u和x的函数关系图

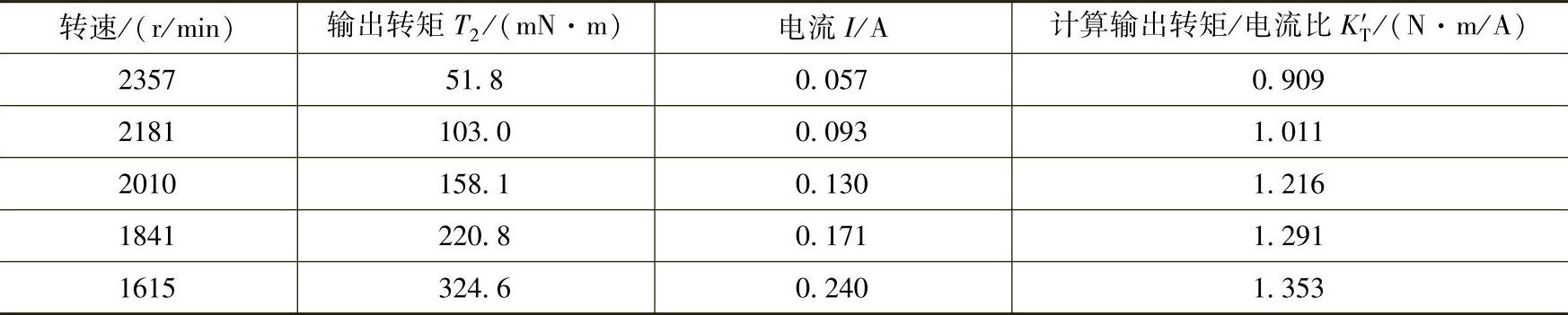
考察一台无刷直流电机样机的输出转矩-电流特性，实测的输出转矩T₂与电流I数据如表4-4所示，并计算输出转矩/电流比K_T′。需要指出，它和K_T转矩系数还有微小差别，因为输出转矩和平均电磁转矩还有一个所谓空载转矩之差。该电机的反电动势系数K_E=1.11V/rad·s^-1。从表可见，随着输出转矩增加，电流增大，转速下降，输出转矩/电流比K_T′逐步在增大，并不是一个常数。这个实例，支持上述对转矩系数K_T大于反电动势系数K_E的分析。

表4-4 实测的输出转矩T₂与电流I数据

下面是K_T/K_E系数比计算的一个例子。

在参考文献[19]给出的电机型号57BL-A-10-30H是磁片表面粘贴转子有槽定子的无刷直流伺服电动机，有关数据见4.4.7节的例1。其中，理想空载转速n₀=5950r/min，K_E=0.528V/rad·s^-1。

参考文献[19]的表2给出仿真计算结果：在转速4468r/min时，输出转矩0.12N·m，电流0.191A，对应的K_T=0.6463。而由样机实测的转矩—电流特性，有K_T≈0.65，表明仿真计算结果接近实际。由此可计算得到K_T/K_E=0.6463/0.528=1.224。

在该负载点（n=4468r/min），K_u=4468/5950=0.751，T=10/pn=0.560ms，x=T/τ=0.230。利用这些数据，按公式（4-32）和式（4-34）计算，得到Kτ=0.2846，K_A=0.2332。再由式（4-36）计算得到K_T/K_E=0.2846/0.2332=1.220。计算结果与参考文献[19]仿真计算的1.224非常接近。这个计算实例表明，所给出的计算公式和函数关系图是可用于工程实际的。