下面的分析是对三相星形六状态工作方式下的无刷直流电机进行，其电机和驱动电路原理图如图4-10所示。

为方便换相过程的分析，作如下假设：

1）三相对称，每相反电动势为梯形波，平顶部分等于120°电角度；

2）忽略开关管和续流二极管的管压降。无刷直流电动机的换相过程的换流时间通常在毫秒级，而开关管本身的关断时间在微秒级，因此完全可以忽略开关管本身关断时间对换流过程的影响；

3）忽略电枢反应、齿槽效应和磁路饱和的影响；

4）相绕组的等效电感为常数；

5）换相过程中电机的转速Ω保持恒定。

三相无刷直流电机的数学模型以矩阵方程表示为

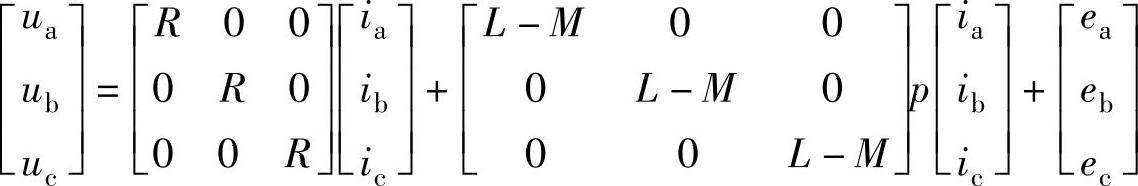
式中，L为相绕组自感，M为相绕组间的互感，假设磁路的磁阻不随转子位置而变化，L和M均为常数。在图4-10中，U为输入到逆变器的直流电源电压，u、e、i分别是各相的绕组端电压、反电动势和电流的瞬时值。并规定相电流以流向绕组中心点为正向电流，相电压以中心点为参考点。为简洁起见，以L代替上式的L-M、R和L为一相的等效电阻和一相的等效电感，电机等效电路的电压平衡方程式改写为

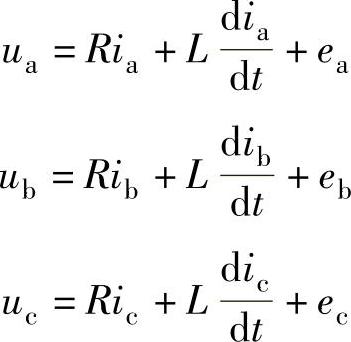
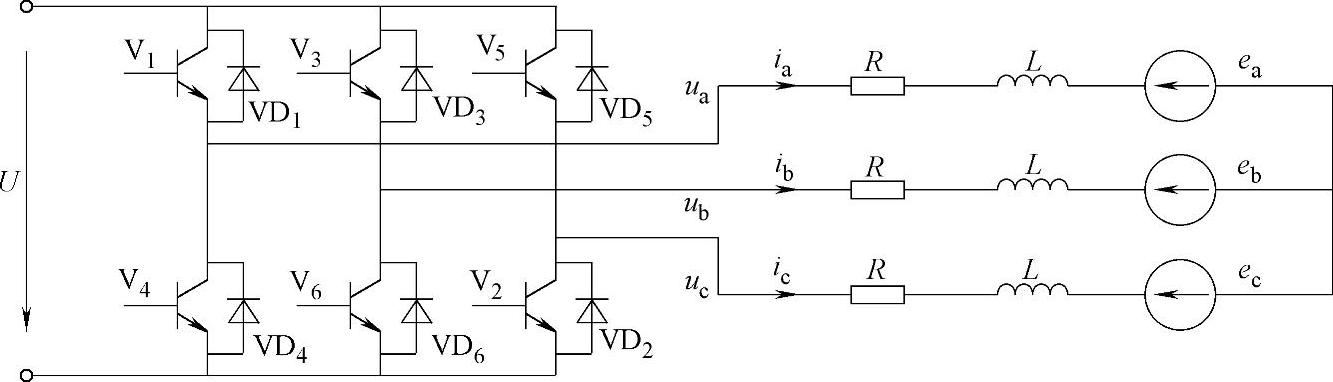
图4-10 三相电机和驱动电路原理图

三相绕组桥式120°导通方式按如下顺序换相：A/B-A/C-B/C-B/A-C/A-C/B。我们讨论电机从A/C相导通向B/C相导通换相过程，以及B/C相导通一个状态角内的有关物理量的变化。参见图4-10和图4-13，电机的换相过程如下：开关V₂保持开通状态不变，C相绕组电流持续，V₁关断的同时V₃开通，B相绕组电流由零开始上升，由于电感的存在A相绕组电流并不能马上降为零，而是通过与V₄反并联的二极管VD₄续流下降，经过一段时间t₁，A相电流降为零。然后，B、C相电流继续增大，经过时间t₂后本周期结束，下一次换相的来临。在图4-13给出一个换相周期T内三相电流变化和A相反电动势波形的示意图。

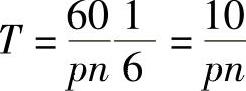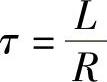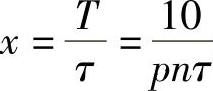B/C相导通状态对应一个状态角60°，一个状态角对应的换相周期时间，它分为两个时间区间：T=t₁+t₂。式中，n为电机转速（r/min），p为极对数。相绕组的电磁时间常数，用表示一个状态角换相周期时间与绕组电磁时间常数的比。

换相过程分两阶段进行，分析如下：

1）第一阶段，时间区间t₁。

这是A相电流关断阶段，从A相的开关V₁关断开始，到A相电流降至零为止。此过程的等效电路如图4-11所示。

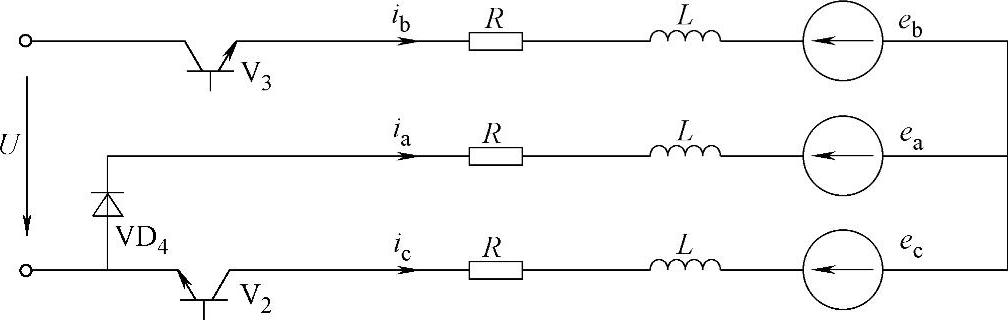
图4-11 时间区间t₁等效电路图

由反电动势为平顶120°的梯形波的设定条件，在B/C相导通的换流过程中，三相绕组的反电动势分别为（A相反电动势波形见图4-13）

根据图4-11所示的等效电路，可列出此阶段的电压平衡方程式为

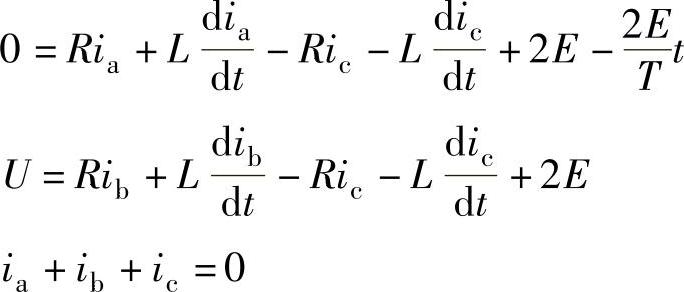
转换为三相电流方程式：

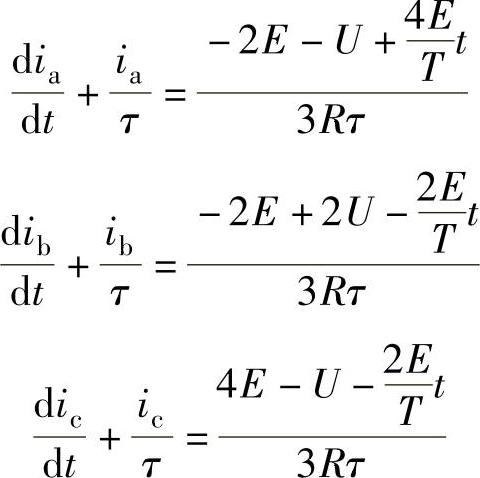
初始条件为

i_a（0）=-i_c（0）=I₀

i_b（0）=0

求取微分方程的解，得到A相电流为

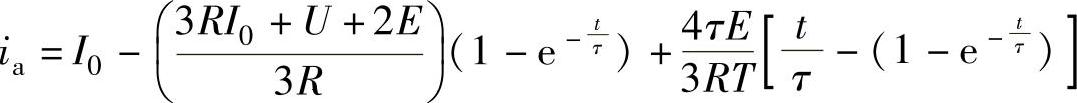(www.daowen.com)

在A相电流降到零的时刻t₁，有

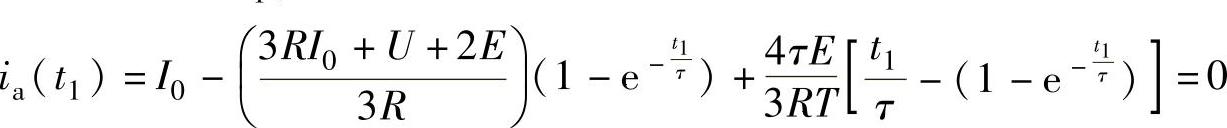
利用近似公式：当α足够小时，有α≈1-e^-α。即附加条件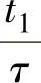：足够小时，有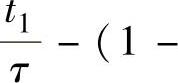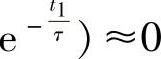，代入上式，得

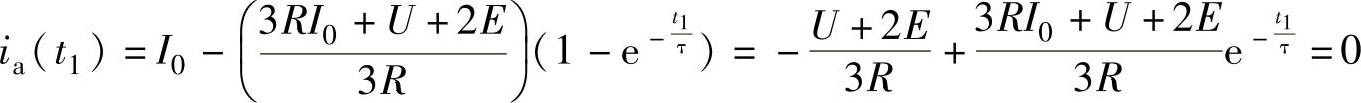
解得A相电流降到零所需要的时间t₁表示为

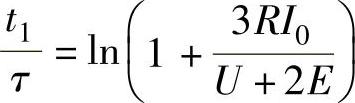
或

同理，A相电流的解简化为

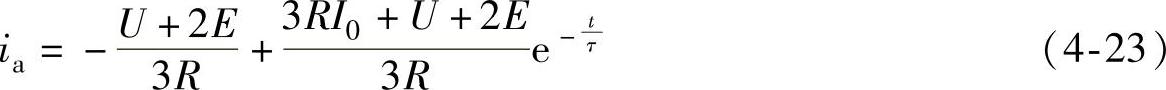
同样，求得B相和C相电流的解为

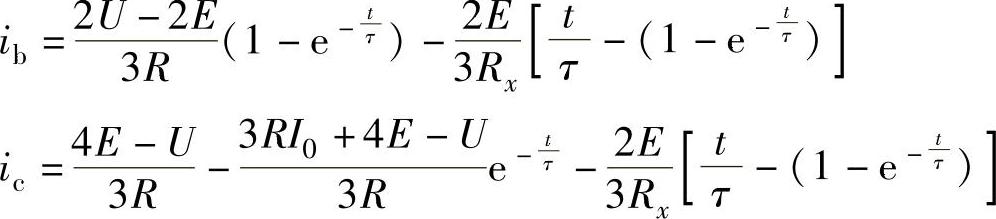
B相和C相电流的解简化为

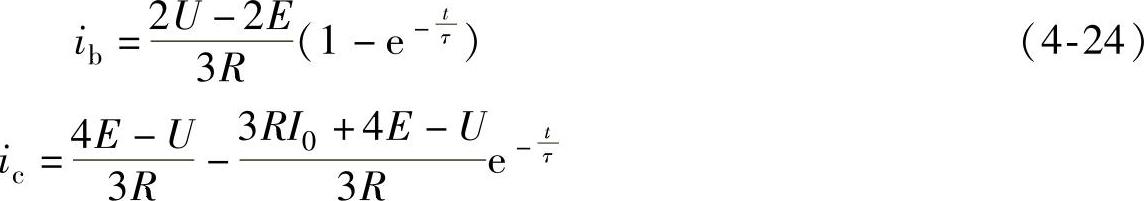
在换相结束时刻t₁时，B相和C相电流值为

2）第二阶段，时间区间t₂。

在此时间区间，A相电路断开，B相和C相电流持续上升，其等效电路如图4-12所示。以A相电流降至零时间为零时刻，由图4-12可列出此阶段的电压平衡方程式为

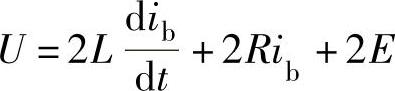
初始条件为 i_b（0）=-i_c（0）=I₁

得B相和C相电流的解：

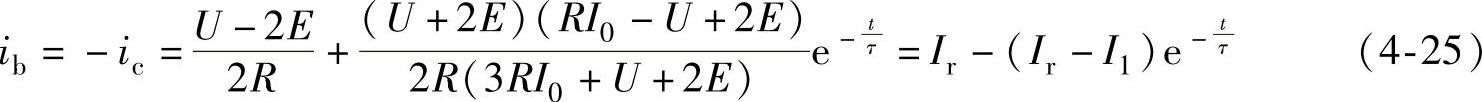
得初始电流的解：

式中，I_r为只计电阻忽略电感时的电流值，。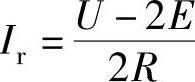

图4-13所示为一个换相周期T内三相电流变化和e_a示意图。

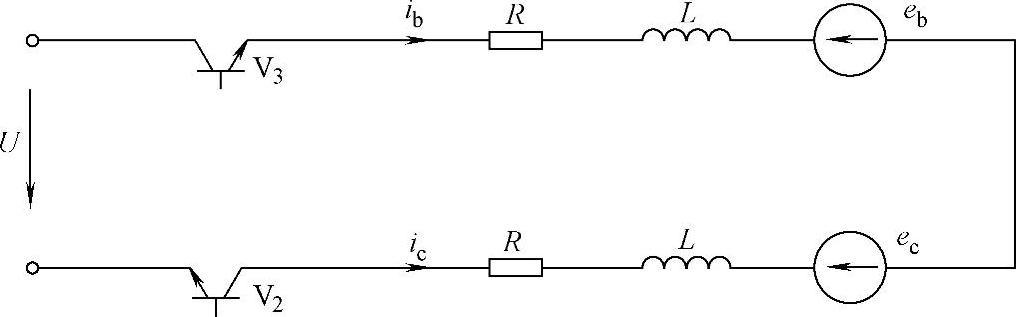
图4-12 时间区间t₂等效电路图

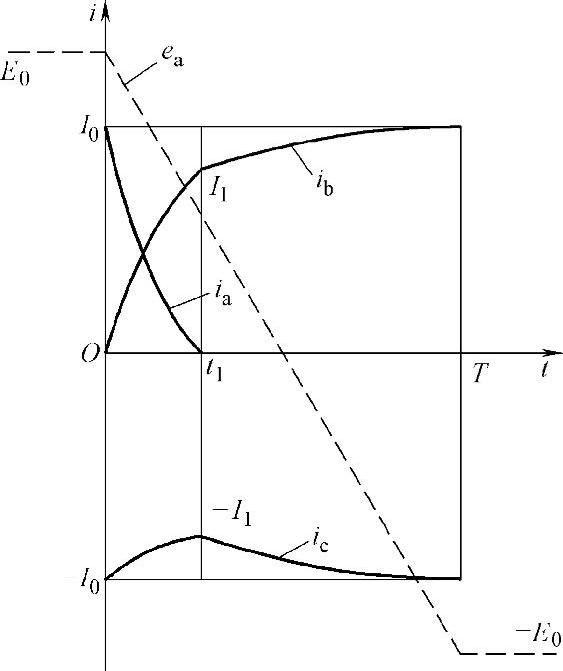
图4-13 一个换相周期T内三相电流变化和e_a示意图