考察实际生产的无刷直流电动机,一个状态角的反电动势波形大多数并非接近平顶波,而更接近正弦波,这是绕组短距和分布的效应,以及几个相绕组合成的效应,使各次谐波明显削弱的缘故。所以,着重研究正弦波反电动势情况是符合实际情况的。参见第6章6.4.1节分析。下面的分析均基于电机反电动势波形为正弦波情况进行分析比较。为了便于对不同的相数、绕组连接和导通方式的比较,忽略了功率开关的电压降。
设反电动势波形函数为余弦函数:
f(θ)=cosθ
并且,θ2=θz/2,θ1=-θz/2。由式(4-12),不同状态角θz下的K2eff和Kav计算结果列于表4-1。
表4-1 K2eff和Kav计算表

利用表4-1数据,由式(4-2)、式(4-4)和式(4-14),转矩系数和反电动势系数按下式计算:

为了比较不同相数绕组的比较判据KD,需要计算它们的绕组系数。设电机为双层整距绕组,短距系数Kp=1。基波分布系数Kd表示为
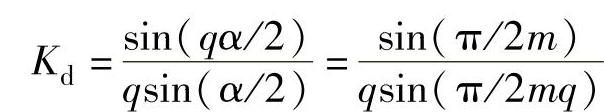
为了统一比较条件,设q足够大,相当于定子有斜槽或转子有斜极,q→∞
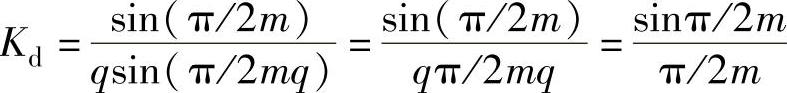
由上式,计算得到表4-2。
表4-2 假设条件下2,3,4相的绕组系数

由式(4-18),比较判据KD按下式计算:

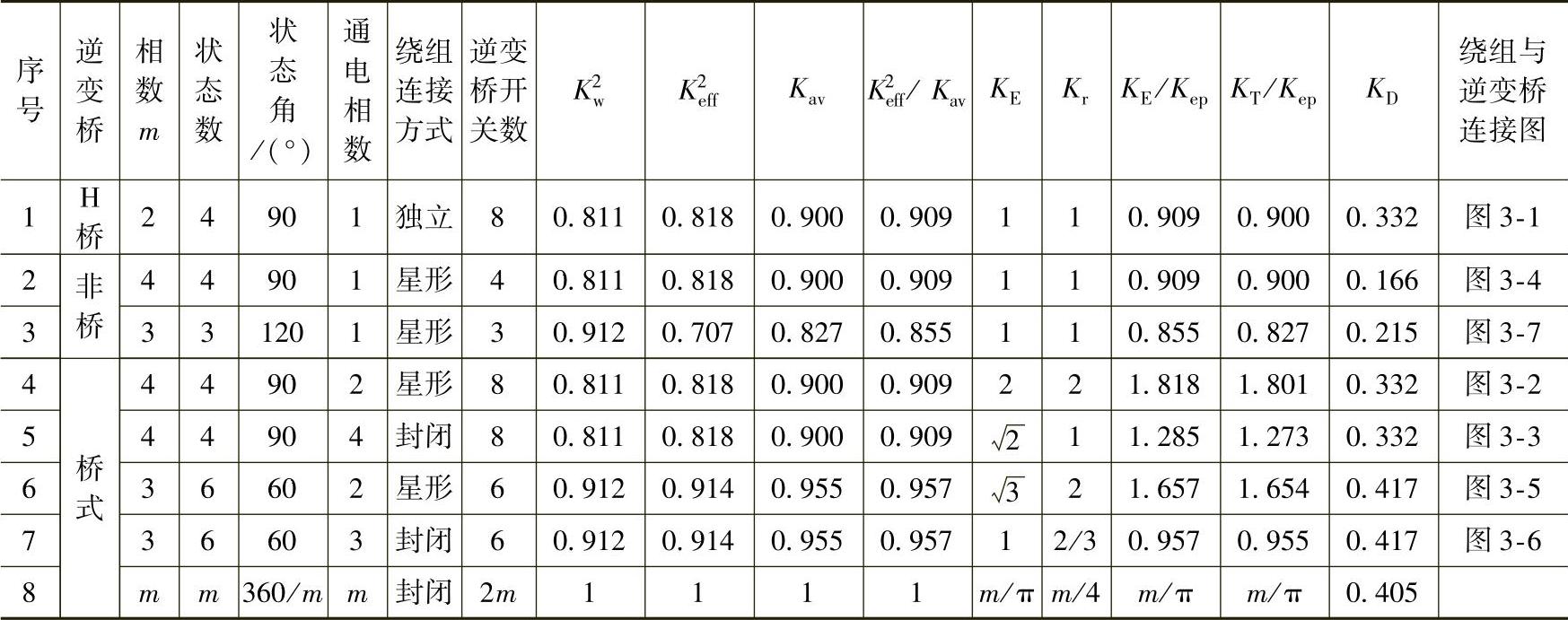
利用上面的公式和数据,分别计算了2,3,4和m相绕组一些典型连接和导通方式的KE/Kep,KT/Kep,KD,结果见表4-3。
以三相桥式绕组为例说明计算过程:
对于星形连接,在一个状态角60°内,有两相绕组串联,它们合成反电动势幅值是一相反电动势幅值的3倍,等效电路的电阻就是两相绕组串联电阻,是一相电阻的2倍,得到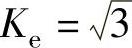 ,Kr=2。KE/Kep=0.9566
,Kr=2。KE/Kep=0.9566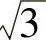 =1.657,KT/Kep=0.9549
=1.657,KT/Kep=0.9549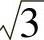 =1.654。KD=0.9135×0.9552×3/(3×2)=0.417。(https://www.daowen.com)
=1.654。KD=0.9135×0.9552×3/(3×2)=0.417。(https://www.daowen.com)
对于三角形连接,在一个状态角60°内,有两相绕组串联再与第三相并联,等效电路的反电动势幅值与一相反电动势幅值相同,等效电路的电阻是一相电阻的2/3倍,得到Ke=1,Kr=2/3=0.6667。KE/Kep=0.9566×1=0.957,KT/Kep=0.9549×1=0.955。KD=0.9135×0.9552×1/3×0.6667=0.417。
两者计算结果都有KD=0.417,完全相同。这说明三相桥式星形连接和三角形连接的性能是相同的,它们有相同的D值,相同的转矩-转速特性斜率。
对于表4-3中的序号8,m相封闭绕组桥式电路,这种工作方式,需要2m个开关,实际意义不大,这是为了与有刷直流电动机作比较,因为它相当于是一台有m个换向片叠绕组的有刷直流电动机。设m为偶数,在电动势波形为正弦的情况下,其反电动势相量图中,m相反电动势形成一个m边多边形。当m足够大时,合成的等效反电动势相当于其外接圆的直径。合成反电动势E与m个相反电动势Ep之和mEp的比就相当于一个圆的直径与周长之比:E/mEp=1/π,即Ke=E/Ep=m/π。等效电路是两个支路的并联,等效电路的电阻比是Kr=m/4。由于状态角很小,K2eff≈1,K2w≈1。计算得到KD=0.405。
利用表4-3数据可以对具体的电机计算其主要参数KE、KT、KD,结合上述有关计算公式即可方便地计算了2、3、4相绕组一些典型连接和导通方式的工作特性。
例如,三相绕组星形联结桥式六状态,由式(4-16)和表4-3序号6的KE/Kep和KT/Kep数据,有
KE≈KT=1.66Kep=1.66KwWpBmDaL×10-4
当不计电感时,按上述规定的单位制,转矩系数KT数值上等于反电动势系数KE。
由式(4-3),理想空载转速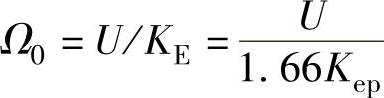
由式(4-1),堵转转矩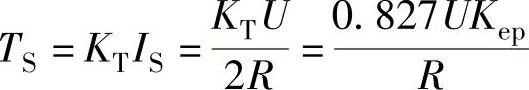
再例如,三相绕组星形联结非桥式三状态,由式(4-16)和表4-3序号3的KE/Kep和KT/Kep数据,有
KE=0.855Kep=0.855KwWpBmDaL×10-4
KT=0.827Kep=0.827KwWpBmDaL×10-4
由式(4-3),理想空载转速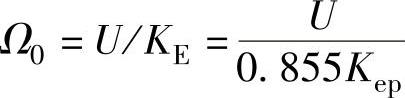
由式(4-1),堵转转矩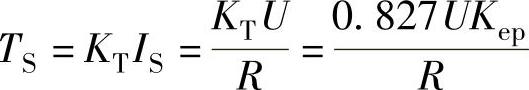
利用计算得的理想空载转速和堵转转矩即可作出电机的电磁转矩-转速特性。由4.1.2节有关公式可计算某一转速点的平均转矩和平均电流。上式中的R是一相绕组电阻值。
从上面两个例子可见,对于同一台三相绕组星形联结的电机,分别按桥式六状态和非桥式三状态工作时,它们的堵转转矩相同,而理想空载转速相差约一倍,机械特性硬度相差约一倍。
表4-3 正弦波反电动势的几种不同相数、不同绕组连接导通方式的计算与比较
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





