值得注意，在理想空载点，平均电磁转矩T_av=0，但由式（4-8），平均电流I_av=I_av0并不等于零，有：

式中，。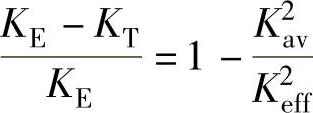

可以证明，在一个状态角内，任意形状的反电动势波形函数f（θ）都有K_eff≥K_av，即有K_E≥K_T。

式（4-8）可以变换为

T_av=K_E（I_av-I_av0）

下面讨论在一个状态角内，反电动势波形函数f（θ）为余弦函数时，空载电流情况。设f（θ）=cosθ

有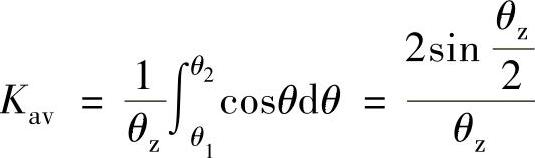

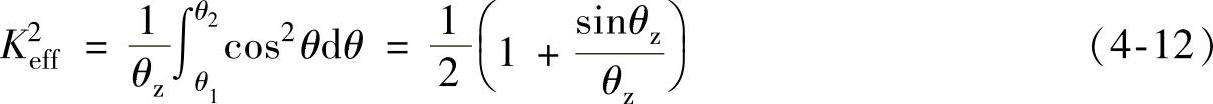
式中，θ₂=θ_z/2，θ₁=-θ_z/2。

例如，在三相六状态工作方式，状态角θ_z=π/3，计算得到K_av=0.9549，K²_av=0.9119，

K²_eff=0.9135，K_T/K_E=K²_av/K²_eff=0.9982，1-K²_av/K²_eff=0.0018。

空载电流平均值 I_av0=0.0018I_s(www.daowen.com)

此时，反电动势幅值为

E_m=K_eqΩ₀=UK_av/K²_eff=1.045U （4-13）

在状态角θ_z=60°内，由于反电动势幅值E_m已稍大于外施电压U，如图4-4所示，从而产生了有正向和负向变化的瞬态空载电流i₀：

i₀=（U-E_mcosθ）/R_eq

实际的空载转速接近于理想空载转速，反电动势大于电压U，也有反向电流产生，它是经过与功率管并联的二极管流通的。并且，理想空载点存在一定的空载电流平均值。这是和有刷直流电机不同点之一。在图4-5给出一台无刷电机空载电流（0.5A）实测示波图，它显示反向电流的存在。

在参考文献[4]给出一台30kW双三相无刷直流电动机一相空载电流的有限元仿真结果和实验实测波形，文中的图6是有限元法仿真一相空载稳态电流，它与图4-4空载电流分析结果相似，它说明这里的瞬态空载电流分析是符合实际情况的。

在这个计算例子，在三相六状态工作方式，理想空载点Ω=Ω₀，空载电流平均值I_av0=0.0018I_s，数值上并不大，工程上完全可以忽略。这样，作为工程实际计算，我们可以认为K_E=K_T。

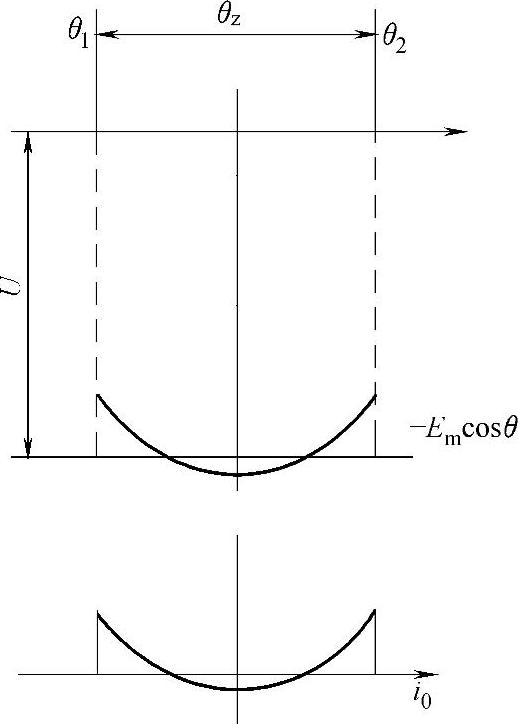
图4-4 理想空载点反电动势幅值E_m和瞬态空载电流i₀

但是，如在第3章3.3.2节的分析中看到那样，在某些情况下理想空载电流的影响会凸现出来。

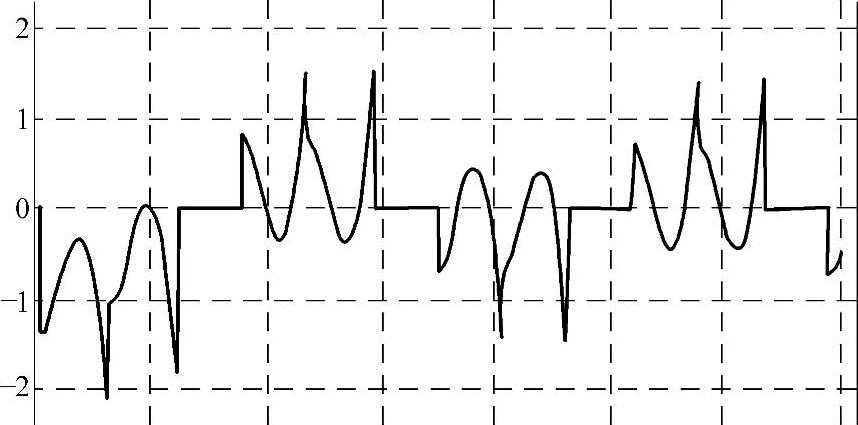
图4-5 0.5A空载电流的实测波形