由基本等效电路图4-1，一个状态角θ_z内的电压平衡方程式为

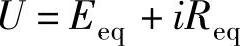
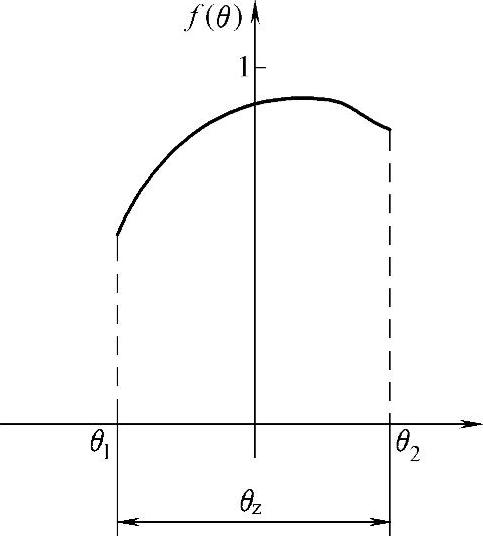
图4-2 反电动势波形函数

考虑到无刷电机可能有不同的反电动势波形，将等效电路的反电动势E_eq以函数形式表示，见图4-2，在状态角θ_z内，有

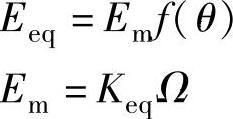
由能量守恒，在状态角θ_z内转子输出的机械功率等于气隙的电磁功率，即

T_eΩ=E_eqi

式中，E_m为反电动势幅值（V）；f（θ）为反电动势波形函数；θ为转子位置电角度；K_eq为等效绕组反电动势系数（V/rad/s）；Ω为转子机械角速度（rad/s）；T_e为电磁转矩瞬时值（N·m）。

由上述各式，得到：

瞬时电流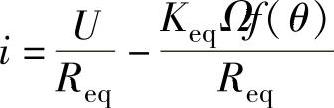

瞬时电磁转矩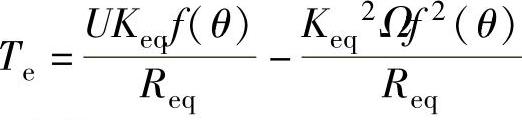

计算在状态角θ_z内的电磁转矩平均值：

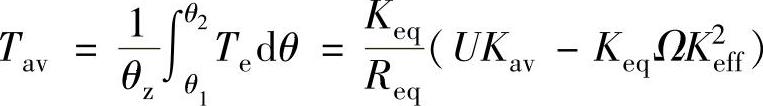
式中K_av为反电动势波形函数f（θ）在状态角θ_z内的平均值系数；K_eff为反电动势波形函数f（θ）在状态角θ_z内的有效值系数。

即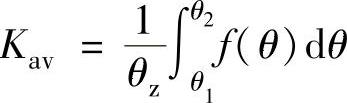

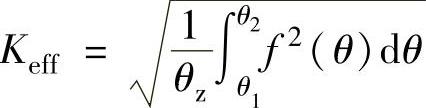
当电机堵转，即转子机械角速度Ω=0时，堵转转矩平均值T_s：

式中，I_s为堵转电流（A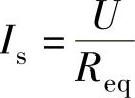），；K_T为转矩系数（N·m/A），

在理想空载点，T_av=0，理想空载转子机械角速度Ω=Ω₀，

式中，K_E为反电动势系数（V/rad·s^-1）(www.daowen.com)

得到无刷直流电动机机械特性通用表达式：

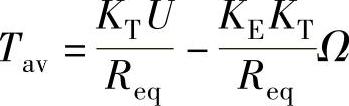
或 T_av=T_s-DΩ

或

式中，D为粘性阻尼系数（N·m/rad·s^-1），。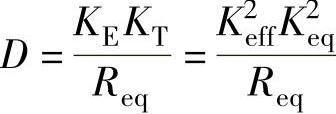

有

式（4-5）表明，无刷直流电动机的机械特性和有刷直流电动机相仿，呈线性关系，见图4-3。并且，在不同外施电压下的机械特性是一族平行直线，机械特性的斜率等于D。

计算在状态角θ_z内的电流平均值为

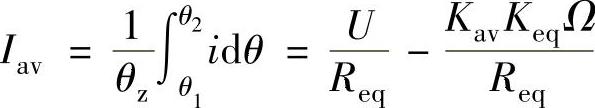
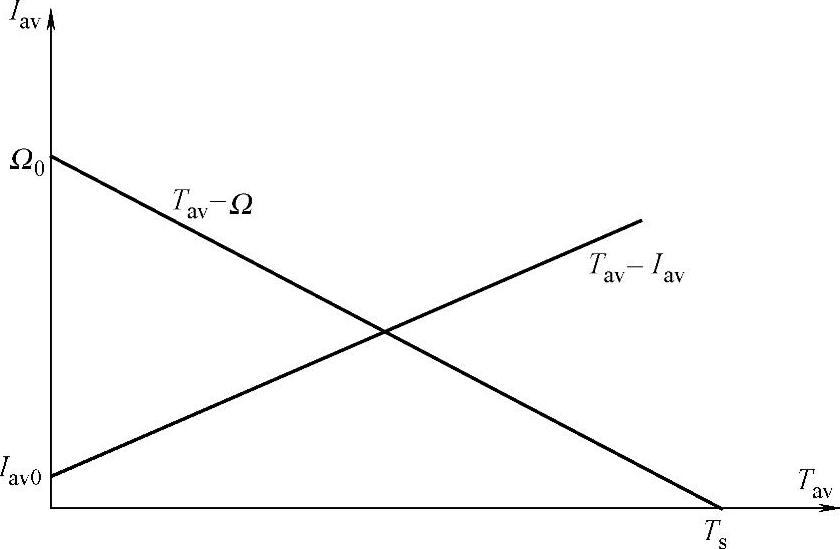
图4-3 无刷直流电动机的机械特性一般形式

上式表明，无刷直流电动机的电流平均值和转速也呈线性关系。并且，在不同外施电压下的特性是一族平行直线。

由式（4-5）和式（4-7），得到平均电磁转矩和平均电流之间也呈线性关系：

T_av=K_EI_av-（K_E-K_T）I_s （4-8）

如下面分析，在三相六状态工作方式，作为工程实际计算，我们可以近似认为K_E≈K_T，上式可以简化为

T_av≈K_EI_av （4-9）

式（4-5）可转换为调节特性表现形式，它显示电机的转速与电压关系：

上式表明，无刷直流电动机的调节特性和有刷直流电动机相仿，也呈线性关系。并且，在不同电磁转矩下电动机的调节特性是一族平行直线。

上述分析表明，在电感可以忽略情况下，无论反电动势波形如何，无论绕组采用什么相数和什么样的连接方式，原理上电子换相无刷直流电动机的基本特性和有刷直流电动机相似，这是电子换相无刷直流电机之所以称为直流电机的基本理由。它们的基本特性都可以用上述统一的公式来表达。