图2-1给出理想情况下，两种电流驱动模式的磁通密度分布、相反电动势、相电流和电磁转矩波形。

无刷直流电动机（BLDC）采用方波电流驱动模式。对于常见的三相桥式6状态工作方式，在360°（电气角）的一个电气周期时间内，可均分为六个区间，或者说，三相绕组导通状态分为六个状态。三相绕组端A、B、C连接到由六个大功率开关器件组成的三相桥式逆变器三个桥臂上。绕组为接法时，这六个状态中任一个状态都有两个绕组串联导电，一相为正向导通，一相为反向导通，而另一个绕组端对应的功率开关器件桥臂上下两器件均不导通。这样，观察任意一相绕组，它在一个电气周期内，有120°是正向导通，然后60°为不导通，再有120°为反向导通，最后60°是不导通的。

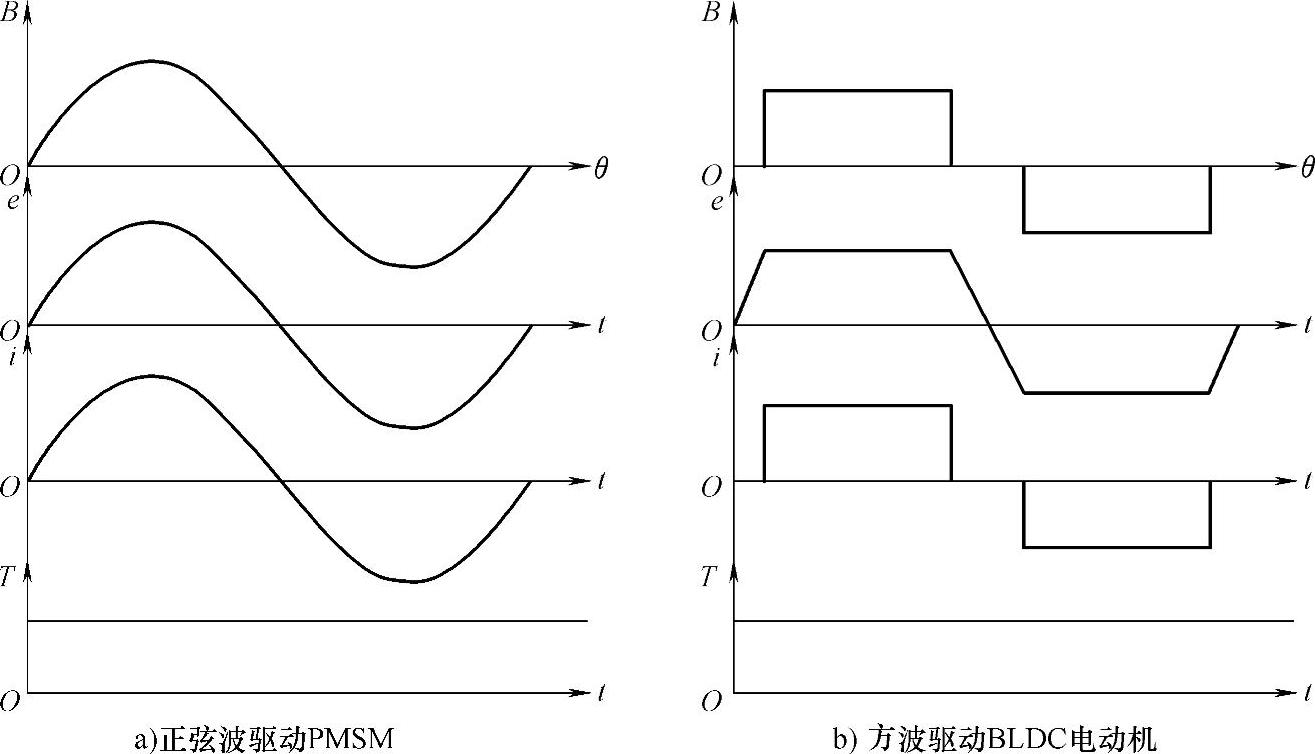
图2-1 理想情况下两种电流驱动模式的磁通密度分布、相反电动势、相电流和电磁转矩波形

首先讨论一相绕组在120°正向导通范围内产生的转矩。当电机转子恒速转动，电流指令为恒值的稳态情况下，由控制器电流环作用强迫该相电流为某一恒值。在理想情况下，无刷直流电机设计气隙磁通密度分布使每相绕组的反电动势波形为有平坦顶部的梯形波，其平顶宽度应尽可能地接近120°。在转子位置传感器作用下，使该相电流导通120°范围和同相绕组反电动势波形平坦部分120°范围在相位上是完全重合的，如图2-1b所示。这样，在120°范围内，该相电流产生的电磁功率和电磁转矩均为恒值。由于每相绕组正向导通和反向导通的对称性，以及三相绕组的对称性，总合成电磁转矩为恒值，与转角位置无关。

在一相绕组正向导通120°范围内，输入相电流I为恒值，它的一相绕组反电动势E为恒值，转子角速度为Ω时，一相绕组产生的电磁转矩为T_ep由下式表示：

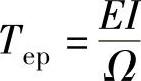
考虑在一个电气周期内该相还反向导通120°，以及三相电磁转矩的叠加，则在一个360°内的总电磁转矩T为

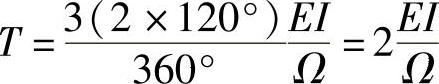(www.daowen.com)

在上述理想情况下，方波驱动永磁无刷直流电动机有线性的转矩-电流特性，理论上转子在不同转角时都没有转矩波动产生。但是，在实际的永磁无刷直流电动机，由于每相反电动势梯形波平顶部分的宽度很难达到120°，平顶部分也不可能做到绝对的平坦无纹波，加上齿槽效应的存在和换相过渡过程电感作用等原因，电流波形也与理想方波有较大差距，转矩波动实际上必然存在。

按正弦波驱动模式工作的永磁同步电动机（PMSM）则完全不同。电动机气隙磁通密度分布设计和绕组设计使每相绕组的反电动势波形为正弦波。正弦波的相电流是由控制器强制产生的，这是通过转子位置传感器检测出转子相对于定子的绝对位置，由伺服驱动器的电流环实现的，并且可以按需要控制相电流与该相反电动势之间的相位关系。它的反电动势和相电流频率由转子转速决定。当相电流与该相反电动势同相时（见图2-1a），三相绕组A、B、C相的反电动势和相电流可表示为

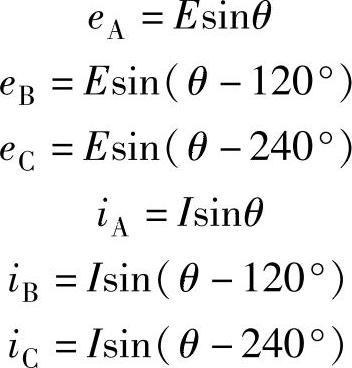
式中，E和I分别为一相反电动势和相电流的幅值；θ为转子转角。这里，它的每相绕组正向导通180°，然后反向导通180°。

电机的电磁功率P和电磁转矩T的关系为

上式表明，正弦波驱动的永磁同步电动机具有线性的转矩-电流特性。式中，瞬态电磁转矩T与转角θ无关，理论上转矩波动为零。在实际的永磁同步电动机中，转矩波动一般比较小。