一、计量抽验的定义及其分类
计量抽验是指对取自检验批的样组中的每个个体,测量其某个定量特性,并用计量值作为批的判定标准的检验方法。例如,纱线断裂强力是以样组断裂强力平均值表示的,并以此来判定检验批的强力是否符合产品标准的规定。在这类问题中,质量指标(记μ0)如单纱强力以及允许的偏差(记Δ)是事先由供需双方共同商定的,或由有关标准所规定的。计量抽验的任务是要根据抽验结果,按统计量¯X是否落在规定的区域μ0±Δ之内,从而作出接受或拒收的判定。计量抽验可按不同准则进行分类如下。
(1)以衡量质量的标志分类,它可以分为以不合格品率P衡量批质量的抽验方案和以母体参数(如μ)衡量批质量的抽验方案。这两种抽验方案是相互联系的,通过P可以计算出所需控制的参数,而由参数也可算出相应的不合格品率P。
(2)以产品规格是否具有上、下公差界限区分,它可分为单侧计量抽验方案和双侧计量抽验方案。单侧是指产品规格中只有单侧公差,验收时只控制一侧;双侧是指产品规格所规定的公差分上限和下限,验收时需要控制双侧。
(3)按母体标准差σ是否已知分类,它可分为σ已知和σ未知两种情况。
(4)按计量抽验形式也可将其分为一次、二次、多次和序贯抽验方案。
二、σ已知时的计量抽验方案
(一)以不合格品率P衡量批质量的抽验方案
1.仅给定规格上限Su时 一批产品的不合格品率P是指检验批中所包含的不合格品数与批量的比值。以仅给出规定上限而论,规定质量特性值X不允许超过给定的规格上限Su,否则以不合格品论处。因此,P即为X>Su这一事件的概率值P(X>Su)。
假定Su已经确定,并由供需双方商定P0和P1值。凡P≤P0的检验批均判定为合格批,其母体均值为μ0,凡P≥P1的检验批均判定为不合格批,其母体均值为μ1。当从某检验中随机抽取一单位产品,测定其质量特性值X,并以此来判定检验批产品质量是否合格时,可能出现以下三种情况(图13-12)。
(1)X在AB间取值,此时应以较高的概率推断该X值是来自均值为μ0的合格批。
(2)X在CD间取值,此时应以较高的概率推断该X值是来自均值为μ1的不合格批。
(3)X在BC间取值,此时难以明确作出接受或拒收的判定。
在上述三种情况中,对于情况(1)和情况(2),我们能对检验批作出明确的判定,从而决定予以接受或拒收。对于情况(3),由于X来自合格批或不合格批的概率相当,所以难以作出接受或拒收的明确判定。同时,由图13-12可知,若X分布的σ越大,则难以作出明确判定的区域BC亦越大。
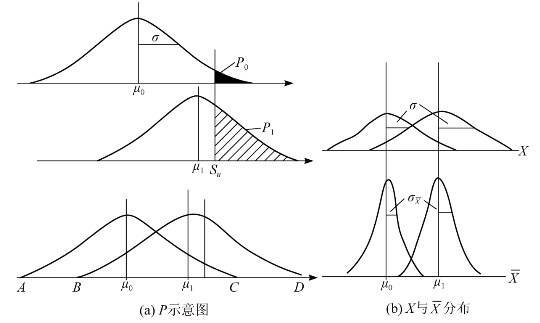
图13-12 仅给定规格上限Su时的方案设计
通常,X服从正态分布,如果从正态母体(μ0,σ)中抽取样组,其样组平均值![]() 服从
服从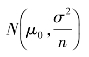 ,即
,即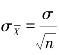 ,
,![]() 不仅比σ小得多,而且可以通过样组的n来调节
不仅比σ小得多,而且可以通过样组的n来调节![]() 的大小。这样,难以作出判断的区域变小了[图13-12(b)]。用
的大小。这样,难以作出判断的区域变小了[图13-12(b)]。用![]() 比X更容易对检验批作出接受或拒收的判定,如果对应于Su而确定了
比X更容易对检验批作出接受或拒收的判定,如果对应于Su而确定了![]() 的判定标准
的判定标准![]() ,那么,检验批的判定准则应为:凡
,那么,检验批的判定准则应为:凡![]() ,则检验批被判为合格批而予以接受;凡
,则检验批被判为合格批而予以接受;凡![]() ,则检验批被判为不合格批而予以拒收。本抽验方案的设计,是在确定α、β、P0和P1的前提下,确定n和Xu。经供需双方商定:凡P≤P0的检验批属合格批,并希望以高概率接受;凡P≥P1的检验批为不合格批,并希望以高概率拒收。如图13-13所示,若P0和P1给定,X服从正态分布,其标准差可以根据长期的生产经验获知(对某一生产工序来说为一定值),则每一条正态分布曲线即代表一检验批。因为P≤P0的检验批均属合格批,而P<P0的检验批有无穷多个,唯有P=P0的检验批是唯一的,所以用P=P0的正态分布曲线代表合格批,其均值为μ0。因此,凡正态分布曲线中的均值μ≤μ0的检验批均属合格批,μ0是合格批的均值最大值。同样地,P=P1的检验批也是唯一的,用P=P1的正态分布曲线代表不合格批,其均值是μ1,μ1是不合格批质量特性均值的最小值。
,则检验批被判为不合格批而予以拒收。本抽验方案的设计,是在确定α、β、P0和P1的前提下,确定n和Xu。经供需双方商定:凡P≤P0的检验批属合格批,并希望以高概率接受;凡P≥P1的检验批为不合格批,并希望以高概率拒收。如图13-13所示,若P0和P1给定,X服从正态分布,其标准差可以根据长期的生产经验获知(对某一生产工序来说为一定值),则每一条正态分布曲线即代表一检验批。因为P≤P0的检验批均属合格批,而P<P0的检验批有无穷多个,唯有P=P0的检验批是唯一的,所以用P=P0的正态分布曲线代表合格批,其均值为μ0。因此,凡正态分布曲线中的均值μ≤μ0的检验批均属合格批,μ0是合格批的均值最大值。同样地,P=P1的检验批也是唯一的,用P=P1的正态分布曲线代表不合格批,其均值是μ1,μ1是不合格批质量特性均值的最小值。
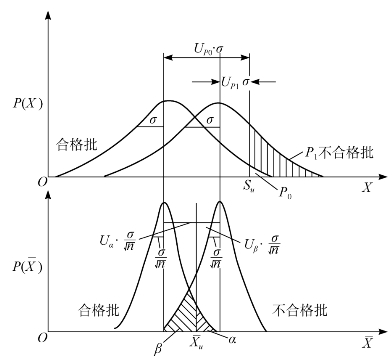
图13-13 方案设计示意图(只有Su)
当以样组![]() 作为判定检验批是否合格的统计量时,图13-13下半部分左侧为从合格批中所抽取样组的
作为判定检验批是否合格的统计量时,图13-13下半部分左侧为从合格批中所抽取样组的![]() 分布曲线,右侧为从不合格批中所抽取样组的
分布曲线,右侧为从不合格批中所抽取样组的![]() 分布曲线,这两条曲线的相交部分(图13-13下半部分阴影区域)为难以作出判断的区域,随着样组n增大,
分布曲线,这两条曲线的相交部分(图13-13下半部分阴影区域)为难以作出判断的区域,随着样组n增大,![]() 值变小,
值变小,![]() 分布曲线越陡,难以作出判定的区域变小。在抽验理论中,相应于Su求得一个适用于
分布曲线越陡,难以作出判定的区域变小。在抽验理论中,相应于Su求得一个适用于![]() 的判定标准
的判定标准![]() ,并规定:凡
,并规定:凡![]() ≤
≤![]() ,则判定该样组所来自的母体为合格批而予以接受;凡
,则判定该样组所来自的母体为合格批而予以接受;凡![]() ,则判定该样组所来自的母体为不合格批而予以拒收。虽然,用
,则判定该样组所来自的母体为不合格批而予以拒收。虽然,用![]() 作为判定检验批合格与否的统计量可以使难以作出判断的区域明显减小,但是,也会造成两种判定错误。
作为判定检验批合格与否的统计量可以使难以作出判断的区域明显减小,但是,也会造成两种判定错误。
(1)犯第一类错误,把合格批错判为不合格批。从图13-13中可以看出,由于抽样的随机性,来自合格批的样组![]() 有可能分布在
有可能分布在![]() 的右侧,则
的右侧,则![]() ,尽管该样组代表的母体是合格批,而根据判定准则规定,因
,尽管该样组代表的母体是合格批,而根据判定准则规定,因![]() ,所以被判为不合格批。犯第一类错误的概率α可以用
,所以被判为不合格批。犯第一类错误的概率α可以用![]() 右侧合格批
右侧合格批![]() 曲线面积大小表示。
曲线面积大小表示。
(2)犯第二类错误,把不合格批错判为合格批。同样,来自不合格批的样组![]() 也可能分布在
也可能分布在![]() 左侧,即
左侧,即![]() ,虽然该样组所代表的母体是不合格批,但依据判定准则规定,因
,虽然该样组所代表的母体是不合格批,但依据判定准则规定,因![]() 而被判作合格批。犯第二类错误的概率β用
而被判作合格批。犯第二类错误的概率β用![]() 左侧不合格批
左侧不合格批![]() 曲线的面积大小表示。
曲线的面积大小表示。
经理论推导,![]() 和n的计算公式如下:
和n的计算公式如下:
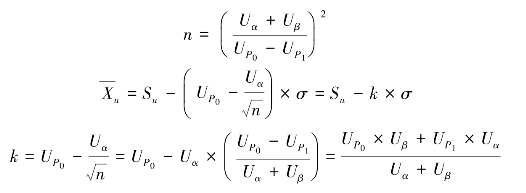
式中:Uα、Uβ、![]() 可以根据相应于的α、β、P0和P1值查阅正态分布上侧分位数表分别求得。
可以根据相应于的α、β、P0和P1值查阅正态分布上侧分位数表分别求得。
2.仅给定规格下限SL时 如图13-14所示,在仅给定规格下限SL情况下,从检验批中抽取大小为n的样组,测量其质量特性值X,并求出其平均值![]() 。据此,凡
。据此,凡![]() ,则判定为合格批而予以接受;凡
,则判定为合格批而予以接受;凡![]() ,则判定为不合格批而予以拒收。它要求质量特性值X越大越好,本方案的设计方法与只给出规格上限Su的情况基本相同,同样可以证明n和
,则判定为不合格批而予以拒收。它要求质量特性值X越大越好,本方案的设计方法与只给出规格上限Su的情况基本相同,同样可以证明n和![]() 的计算分别为:
的计算分别为:
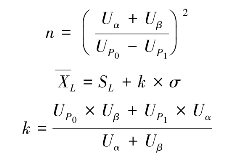
(二)以母体均值μ衡量批质量时的抽验方案
1.仅给定规格上限Su时 对有些产品,希望其质量特性值的均值![]() 越小越好,亦即仅给定规格上限Su。若仅给定规格上限Su时,设产品的质量特性值X服从正态分布N(μ,σ2),并希望X的母体均值μ越小越好。因此规定:凡检验批均值μ小于或等于某个预先指定的上限值μ0,即μ≤μ0时,则认为该批产品为合格批,并希望以不低于1-α的高概率接受;凡检验批均值μ大于或等于某一定值μ1(μ1>μ0),即μ≥μ1时,则认为该检验批为不合格批,并希望以不超过β的低概率接受,亦即以大于1-β的高概率拒收。其示意图见图13-15。
越小越好,亦即仅给定规格上限Su。若仅给定规格上限Su时,设产品的质量特性值X服从正态分布N(μ,σ2),并希望X的母体均值μ越小越好。因此规定:凡检验批均值μ小于或等于某个预先指定的上限值μ0,即μ≤μ0时,则认为该批产品为合格批,并希望以不低于1-α的高概率接受;凡检验批均值μ大于或等于某一定值μ1(μ1>μ0),即μ≥μ1时,则认为该检验批为不合格批,并希望以不超过β的低概率接受,亦即以大于1-β的高概率拒收。其示意图见图13-15。
抽验是用样组均值![]() 作为判别接受与否的统计量,
作为判别接受与否的统计量,![]() 的分布曲线如图13-15的下半部分所示,相应于μ0和μ1,求得一个适用于
的分布曲线如图13-15的下半部分所示,相应于μ0和μ1,求得一个适用于![]() 的判别界限
的判别界限![]() ,其判定准则为:凡
,其判定准则为:凡![]() ,则检验批被判为合格批而予以接受;
,则检验批被判为合格批而予以接受;![]() ,则检验批被判为不合格批而予以拒收。但是,由于抽样的随机性,同样也会犯第一类错误和第二类错误,其概率值分别为α和β。α和β值一般由供需双方事先商定,通常取α=0.05,β=0.10。
,则检验批被判为不合格批而予以拒收。但是,由于抽样的随机性,同样也会犯第一类错误和第二类错误,其概率值分别为α和β。α和β值一般由供需双方事先商定,通常取α=0.05,β=0.10。
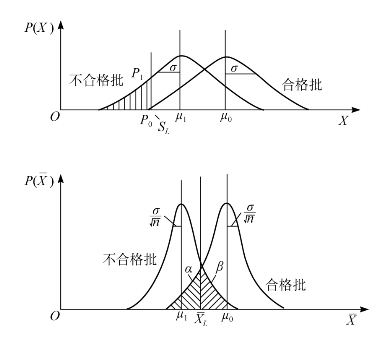
图13-14 方案设计示意图(只有SL)
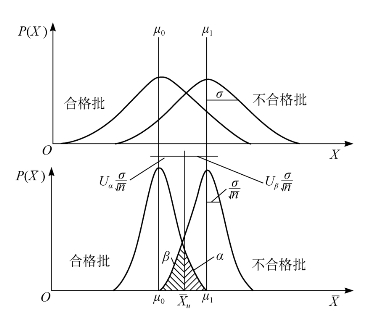
图13-15 以μ衡量批质量时方案设计(只有Su)
本抽验方案的设计,是在μ0、μ1、α和β确定的前提之下,确定n和![]() 值。经理论推导,n和
值。经理论推导,n和![]() 的计算公式分别为:
的计算公式分别为:
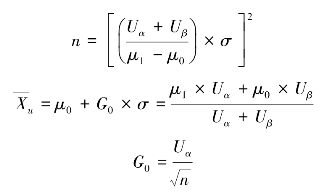
式中:Uα和Uβ可根据α和β值查正态分布上侧分位数表求得。为使抽验量n不至于过大,在规定μ0和μ1时,应注意μ0和μ1不能过分接近。
【例题】为了验收一批产品,经供需双方商定,α=0.05,β=0.10,μ0=70,μ1=73,根据以往的统计资料获知σ=2,求满足上述条件的计量一次抽验方案。
解:因为Uα=U0.05=1.645,Uβ=U0.10=1.282
而 μ0=70,μ1=73,σ=2
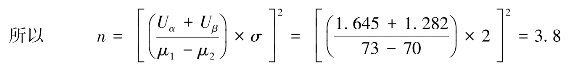
取n=4。
则
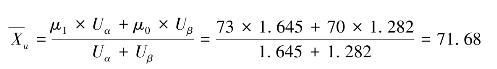
故所求方案为:n=4,![]() ,即从批中随机抽取4个单位产品,测量其质量特性值,并求得平均值
,即从批中随机抽取4个单位产品,测量其质量特性值,并求得平均值![]() 。若
。若![]() ,则判定该批产品为合格批而予以接受;若
,则判定该批产品为合格批而予以接受;若![]() ,则判定该批产品为不合格批而予以拒收。
,则判定该批产品为不合格批而予以拒收。
2.仅给定规格下限SL时 如图13-16所示,在α、β、μ0和μ1(μ1<μ0)给定的条件下,经理论推导,n和![]() 的计算公式分别为:
的计算公式分别为:
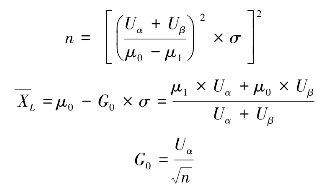
在仅给定规格下限条件下,其判定准则为:当![]() 时,判定为合格而予以接受;当
时,判定为合格而予以接受;当![]() 时,判定为不合格而予以拒收。
时,判定为不合格而予以拒收。
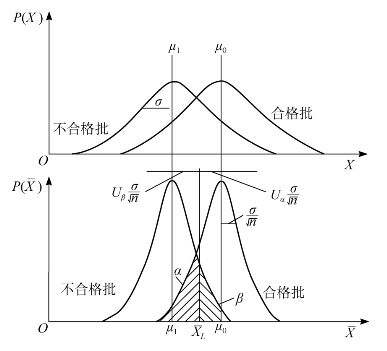
图13-16 以μ衡量批质量时的方案设计(只有SL)
三、σ未知时的计量抽验方案
(一)σ未知时统计量的分布特点
由于种种原因而不能精确地估计母体标准差σ的时候,应把σ估计的不准确性因素考虑在内。假定从μ=μ0的正态母体中抽取容量大小为n的样组,其均值应为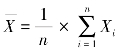 ,无偏标准差为
,无偏标准差为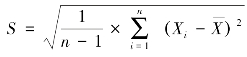 ,按t分布的定理可知:
,按t分布的定理可知: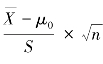 服从t(n-1)分布。当我们从μ=μ1的正态母体中抽取一个容量大小为n的样组时,由于随机变量
服从t(n-1)分布。当我们从μ=μ1的正态母体中抽取一个容量大小为n的样组时,由于随机变量![]() 服从均值为μ1-μ0(μ1-μ0≠0),标准差为
服从均值为μ1-μ0(μ1-μ0≠0),标准差为![]() 的正态分布,即服从
的正态分布,即服从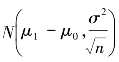 。
。
而又知: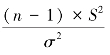 服从X2分布(自由度ν=n-1)。因此,
服从X2分布(自由度ν=n-1)。因此,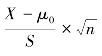 服从自由度ν=n-1的非中心t分布。
服从自由度ν=n-1的非中心t分布。
如上所述,要从μ=μ0时![]() ,以及μ=μ1时
,以及μ=μ1时![]() β两式中求得n和k,需利用t分布表和非中心t分布表,那将是十分麻烦的。由正态分布的性质可知,当n较大(n≥5)时,S的分布近似服从正态分布
β两式中求得n和k,需利用t分布表和非中心t分布表,那将是十分麻烦的。由正态分布的性质可知,当n较大(n≥5)时,S的分布近似服从正态分布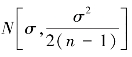 ,而
,而![]() 也服从正态分布
也服从正态分布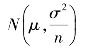 ,且可以证明
,且可以证明![]() 和S相互独立,所以
和S相互独立,所以![]() 亦服从正态分布N
亦服从正态分布N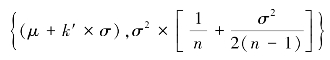 。
。
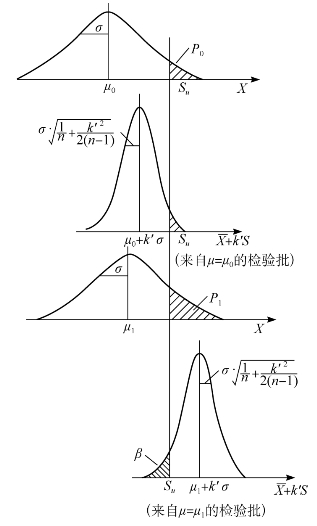
图13-17 σ未知方案设计示意图(仅有Su)(www.daowen.com)
(二)以P衡量批质量时的抽验方案1.仅给定规格上限Su时 在σ已知并给出Su时,前面已经指出:当![]() 时,检验批被判为合格批而予以接受;当
时,检验批被判为合格批而予以接受;当![]() 时,则检验批被判为不合格批而予以拒收。如果将上述判定规则改变为:若
时,则检验批被判为不合格批而予以拒收。如果将上述判定规则改变为:若![]() ,则判定检验批合格;若
,则判定检验批合格;若![]() ,则判定检验批不合格。现在的情况是σ未知,若用无偏标准差S估计σ,则对σ未知的判定准则又可变更为:若
,则判定检验批不合格。现在的情况是σ未知,若用无偏标准差S估计σ,则对σ未知的判定准则又可变更为:若![]() ,予以接收;若
,予以接收;若![]() ,予以拒收。
,予以拒收。
现在假定:凡具有P0且母体均值为μ0的检验批作为合格批而以1-α的高概率接受;凡具有P1且母体均值为μ1的检验批作为不合格批而以高概率1-β拒收。由于抽样的随机性,犯第一类错误和第二类错误的概率分别规定为α和β,如图13-17所示。
从来自μ=μ0检验批中的![]() 分布曲线中:
分布曲线中:
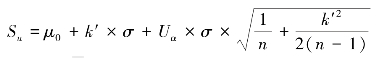
从来自μ=μ1检验批中的![]() 分布曲线中:
分布曲线中:
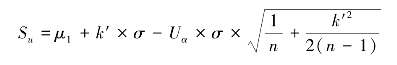
由公式可知:
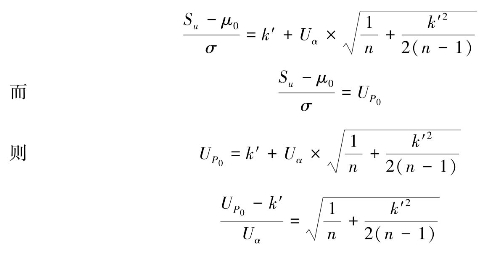
同理可得:
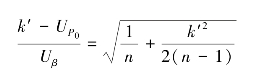
由公式可求得:
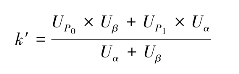
此k′在数值上与σ已知时的判定系数k是一致的(k′=k),为了简化计算,若令n-1≈n(n较大场合),则可以求得:
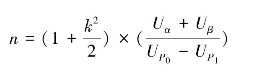
【例题】假定σ未知,技术标准规定:当单位产品的质量特性值X不超过500为合格品,又规定:P0=1%,P1=10%,α=0.05,β=0.10,求满足这些条件的计量一次抽验方案。
解:因为P0=1%,P1=10%,α=0.05,β=0.10,查正态分布上侧分位数表可得:![]() =2.33,
=2.33,![]() ,Uα=1.64,Uβ=1.28。
,Uα=1.64,Uβ=1.28。
又知Su=500。
所以
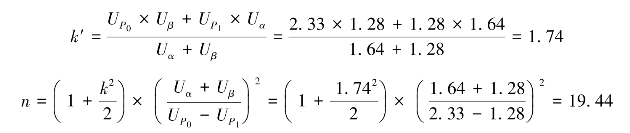
取n=20。
故所求方案为:从检验批中一次抽20个单位产品,测定其质量特性值X,求出平均值![]() 和无偏标准差S,其判定准则如下。
和无偏标准差S,其判定准则如下。
若![]() 时,该检验批被判为合格批而予以接受;
时,该检验批被判为合格批而予以接受;
若![]() 时,该检验批被判为不合格批而予以拒收。
时,该检验批被判为不合格批而予以拒收。
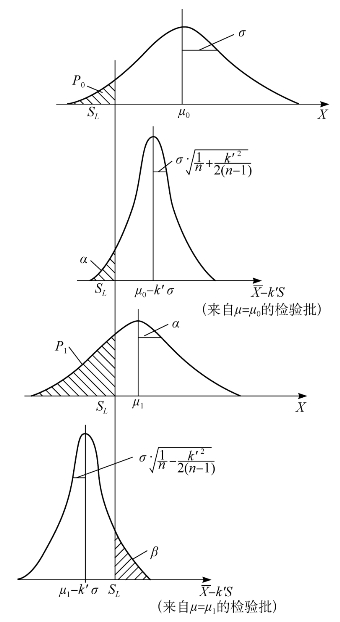
图13-18 σ未知时的方案设计(只有SL)
2.仅给定规格下限SL时 如图13-18所示,与仅给定规格上限Su的情况基本相同,理论上同样可以证明n和k′的计算公式仍为:
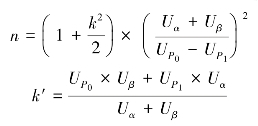
且k=k′。
对于σ未知而以样组无偏标准差S作为统计量的判定准则如下。
若![]() 时,判定检验批为合格批而予以接受;
时,判定检验批为合格批而予以接受;
若![]() 时,判定检验批为不合格批而予以拒收。
时,判定检验批为不合格批而予以拒收。
(三)以均值μ衡量批质量时的抽验方案
1.仅给出规格下限SL时 如前所述,
在给定规格下限SL情况下,我们希望检验批质量特性值X的母体均值μ愈大愈好。若X服从正态分布N(μ,σ2),且σ已知时,样组均值![]() 服从
服从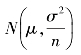 分布。作为检验统计量的
分布。作为检验统计量的![]() 不能比合格批母体均值μ0小得太多,按正态分布的性质,我们可以设某一定值k′,使得:
不能比合格批母体均值μ0小得太多,按正态分布的性质,我们可以设某一定值k′,使得: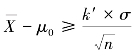 ,即
,即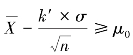 时,判定检验批为合格批而予以接受;
时,判定检验批为合格批而予以接受;![]()
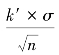 ,即
,即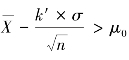 时,判定检验批为不合格批而予以拒收。
时,判定检验批为不合格批而予以拒收。
在母体标准差σ未知场合下,假如用样组无偏标准差代替σ,相应的判定准则为:凡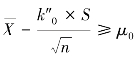 时,检验批被判为合格批而予以接受;凡
时,检验批被判为合格批而予以接受;凡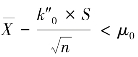 时,检验批被判为不合格批而予以拒收。
时,检验批被判为不合格批而予以拒收。
若令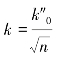 ,那么判定准则又变更为:若
,那么判定准则又变更为:若![]() 时,判定合格;若
时,判定合格;若![]() 时,判定不合格。
时,判定不合格。
如前所述,当样组n较大时,来自μ=μ0母体的随机变量![]() 的分布近似服从
的分布近似服从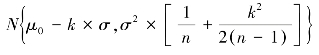 ;来自μ=μ1母体的随机变量
;来自μ=μ1母体的随机变量![]() 的分布近似服从
的分布近似服从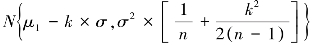 。所以,本抽验方案应满足的条件为:
。所以,本抽验方案应满足的条件为:
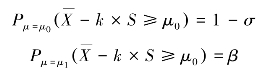
由图13-19可知:
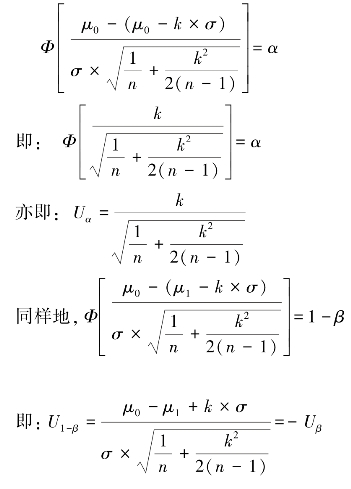
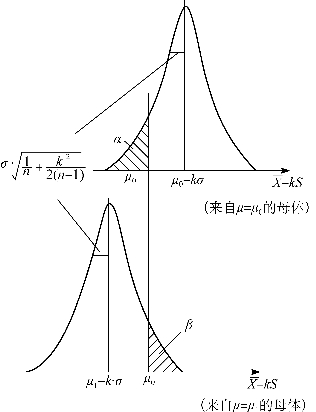
图13-19 σ未知,以μ衡量批质量时的方案设计(只有SL)
当n很大,![]() 时,公式可分别写成:
时,公式可分别写成:
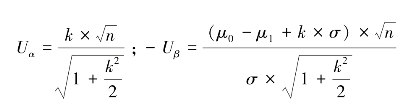
由此可以求得n和k的计算公式分别为:
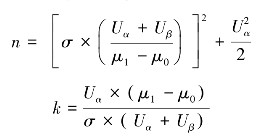
从上面的公式中可以得出如下结论。
(1)虽然我们所讨论的是σ未知情况,而公式中却出现了σ,在此情况下,我们可以利用过去的资料给出σ的估计值。
(2)同σ已知时的样组容量n计算公式相比较,公式增加了![]() 这一项,可见,当α减小时,Uα的绝对值增大,而使n值增大。
这一项,可见,当α减小时,Uα的绝对值增大,而使n值增大。
【例题】现有一批织物,已知其强力服从正态分布,且根据以往试验结果得知强力标准差σ的估计值为1.5N,同时规定μ0=300N,μ1=270N,α=0.05,β=0.10,求满足上述条件的计量一次抽验方案。
解:查正态分布上侧分位数表可知,
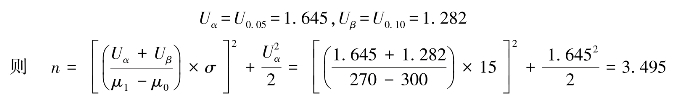
取n=4。
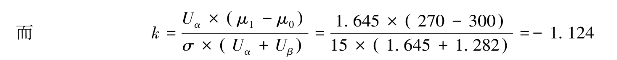
因此,该计量一次抽验方案为:从批中抽取4个单位产品,测量其强力,并计算样组平均值![]() 和无偏标准差S,若
和无偏标准差S,若![]() ,则接受该检验批,若
,则接受该检验批,若![]() ,则拒收该检验批。
,则拒收该检验批。
2.仅给出规格上限Su时 在此情况下,判定准则为:凡![]() ,判定合格而予以接受;凡
,判定合格而予以接受;凡![]() 时,判定不合格而予以拒收。同样可以证明,n和k的计算公式分别为:
时,判定不合格而予以拒收。同样可以证明,n和k的计算公式分别为:
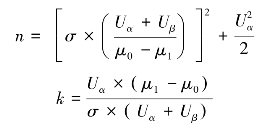
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






