一、计数抽验的定义

计数抽验是对取自检验批的样本中每个个体记录有无某种属性，计算共有多少个体具有（或无）这种属性，或者是计算每个（或每百个）个体中的缺陷数的检查方法。例如，生丝匀度检验是以受验丝片中出现的一度变化、二度变化和三度变化的条数来判定生丝均匀度优劣程度的；毛织物外观质量分别按散布性外观疵点和局部性外观疵点结辫率表示。

二、抽样方案的操作特性曲线

（一）样组中不合格品个数为d的出现概率

图13-2　抽验示意图

如图13-2所示，设批量大小为N的批中，含有D个不合格品，则该批中出现D个不合格品的概率为。若从该批中随机抽取n个单位产品，则在该样组中出现d个不合格品的概率Pn（d）可按超几何分布公式计算，即

当N无限大或N虽有限，但时，公式可用二项分布近似计算，即

如果，且P＜0.1，n·P为一有限数时，Pn（d）又可以用泊松分布近似计算，即

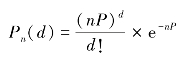
（二）检验批被接受的概率

假定从批中抽取大小为n的样组，样组中可允许的缺陷个数为C，则在方案（n/C）已确定的条件下，该批产品被判为“合格批”的事件等价于d取值从0至C为止的，C+1个不相容事件之和。所以，检验批被接受的概率PA的计算公式应为：

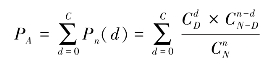
式中：PA——检查批被接受的概率；

N——批量大小；

C——样组中可允许的缺陷个数；

n——样组数；

d——不合格品数。

（三）抽验方案的操作特性函数

在一定条件下，PA可用泊松分布公式近似计算（其具体计算可以查阅有关附表或桑迪克曲线），计算公式可写为：

例如，N=10万的某一批产品用（100/15）方案进行计数抽验，当P=10%时，因为nP=10，则

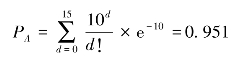
计算结果表明：在本抽验方案下，该批产品被判为合格批的概率为95.1%。

由于单位产品的缺陷数一般都服从泊松分布P（d，λ）的，所以n个单位产品的总缺陷数也应服从泊松分布P（d，nλ），当样组中可允许的缺陷个数C和n/C均已确定时，则

可以看出，当以批不合格品率P衡量批质量时，相对于一定的抽验方案（n/C），由于检验批被接受的概率PA与N基本无关，所以它仅依赖于P值，即PA的值仅仅是P的函数。虽然，采用不同的抽验方案验收、检验批质量时，批被接受的概率PA都是P的函数，但对应于不同方案的L（P）形式并不相同，如

方案为（4/0）：

方案为（4/1）：

事实上，不同的L（P）函数形式能够反映出不同抽验方案的操作特性，即能够反映出不同抽验方案对检验批质量优劣的鉴别能力。

图13-3　OC曲线

（四）抽验方案操作特性曲线——OC曲线

抽验方案操作特性曲线，即OC曲线又称抽样检验动能曲线或接受概率曲线，它表示在某一特定抽验方案（n/C）下的检验批被接受概率PA与批不合格品率P之间的关系曲线。如图13-3所示，纵坐标为PA，亦即L（P），横坐标为P，对应于不同的抽验方案（n/C），就有与其对应的不同的OC曲线。

结合抽验方案操作特性函数，分析OC曲线可以得出：

（1）当P=0时，即检验批中所有产品均是合格品，那么，无论采用何种抽验方案（n/C），该检验批被判为合格而予以接受的概率L（P=0）=1.0。

（2）当P=100%时，即检验批中所有产品均为不合格品，那么，无论采用何种抽验方案（n/C）都将拒收该批产品，即L（P=100%）=0。

（3）一般情况下，L（P）的值总是介于0和100%之间的，而且P值越接近于0，检验批经抽样检验被判为合格批的可能性也越大。

一个理想的抽验方案应该是：当P≤P0时，L（P）=1，即该检验批肯定被判为合格批；当P＞P0时，L（P）=0，即该检验批肯定被判为不合格批。图13-4所示为理想方案的OC曲线，而实际情况并非如此，理想的抽验方案是不存在的，采用抽样检验供需双方都要承担一定风险。

一个有较强判断能力抽验方案的OC曲线应具有以下两个特点（图13-5）：

（1）当P≤P0时，应以高概率判定其合格而予以接受。

（2）当产品质量变差，L（P）应陡减，在P≥P1时，则应以高概率判定其不合格而予以拒收。

图13-4　理想方案的OC曲线

图13-5　典型的OC曲线

三、计数抽验的形式

计数抽验或计量抽验的形式按抽取样本的次数均可分为一次抽验、二次抽验和多次抽验三种不同的抽验形式。

（一）一次抽验

一次抽验又称单式抽验或一回抽验，它仅仅是从检验批中抽取一个样本，根据样组检查的结果，判定该检验批为合格予以接受或不合格予以拒收，其操作原理如图13-6所示。一次抽验方案由n和c两个参数决定。

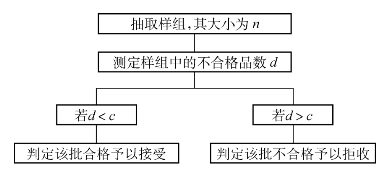
图13-6　一次抽验操作原理示意图

（二）二次抽验

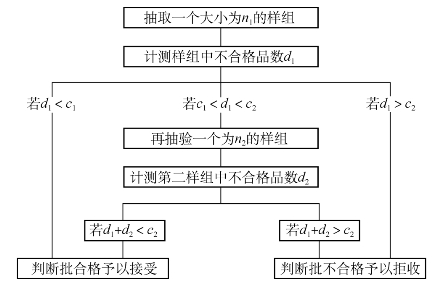
二次抽验是在一次抽验基础上形成的另一种抽验形式。所谓二次抽验，就是指最多抽取两个样组作出判定的一种抽验形式，其操作原理见图13-7。采用二次抽验形式并不一定每批都必须抽取两个样组，假如通过第一样组就可以作出合格与否的判断，则不必再抽取第二样组。因此，二次抽验的平均检验量要小于一次抽验。通常，二次抽验方案由n1、n2、c1和c2四个参数确定，其中：c2＞c1+1，n1比一次抽验的n要小，而n2相对于n1的最佳比值是一个十分困难的统计问题，如果n1≈n2，检验量最小，故在二次抽验方案中，一般取n1=n2。

(www.daowen.com)

图13-7　二次抽验操作原理示意图

（三）多次抽验

多次抽验也称多回抽验，它是一种允许抽取两个以上的具有同等大小n的样组（通常n相同，但非必要）方能最终作出对检验批接受或是拒收判定的抽验方式，其操作原理如图13-8所示。应该注意的问题是：Rei＞Aci+1，待至最后一样组，Rek=Ack+1；抽验不一定要进行到k次才中止；多次抽验的抽验量一般为一次抽验的，而且通常总是小于二次抽验方案的。

图13-8　多次抽验操作原理示意图

（四）序贯抽验

序贯抽验最早是由罗马尼亚数学家华尔德在第二次世界大战中发明的，由于其检验量小，特别适用于军火的破坏性检验。序贯抽验是每次仅抽取一个单位产品的逐项抽验。逐项抽验也称逐次、逐个抽验，这种抽验方案并不限制抽验次数，每次从抽验批中仅抽出一个单位产品进行试验，然后作出合格、不合格或继续抽验的判定，直到能作出批合格与否的判定时才停止抽验。

四、百分比抽验的不合理性

（一）单百分比抽验

我国纺织产品验收检验曾普遍采用百分比抽样，最早的方案为单百分比抽验，即无论检验批的批量大小N为何值，均按同一个百分比Kn抽取样组，而对样组的合格判定数C则保持不变。这种抽样方案貌似公正合理，但不科学。当批质量相同即合格判定数不变时，由于单百分比抽验容易造成对大批过严，而对小批过宽的不合理现象，而且对大批量产品抽取的样本过大，难以体现抽样检验的经济性，所以单百分比抽样方案已被其他先进的抽样方案所替代。

单百分比抽验示例如图13-9所示。在此方案中，若按10%的同一比例进行抽样，当N分别为50、100、200和1000时，相应的样组n大小分别为5、10、20和100，而这四批产品的合格判定数C均为零，这四个方案的OC曲线如图13-9所示。

图13-9　单百分比抽验示例

（二）双百分比抽验

表13-1列举了我国目前主要纺织产品的抽样方案，其中：内在质量各项指标均以平均值作为合格判定数，平均值在标准规定值范围以内者为合格批（染色牢度以批抽样的2/3及2/3以上符合者为合格批）。从表13-1中可以看出：我国现行的纺织产品抽样验收和检验中，以有一定限度的双百分比方案为主，各类产品可根据各自的特点而有所差别。双百分比抽验比单百分比抽验方案有所改进，也能反映长期连续生产的产品质量，但其不合理性依然存在。所以，有些产品如丝织物验收检验已废弃了这种不合理的抽验方案，转而采用较为合理的计数一次抽样方案，其依据为GB 2828标准。

双百分比抽验，即以检验批量N为基础，按一定百分比Kn抽取样组，同时合格判定数C亦随样组大小n而成比例地变化。双百分比抽验从表面上看似乎要比单百分比抽验更加合理，但也不能从根本上克服百分比抽验的不合理性，即对于大批量方案过严，而对于小批量方案过宽。

表13-1　我国主要纺织产品现行抽样方案

续表

（三）复式抽验——加倍抽验

图13-10　复式抽验操作示意图

我国纺织产品现行抽验方案中，还有一种经常采用的加倍抽验方案，即复式抽验方案，复式抽验的操作示意图如图13-10所示。采用复式抽验时，第一次抽取n1个样品，，从n1中检测到d1个不合格品。若d1=0，则判定其为合格批而予以接受；若d1≥2，则判定其为不合格批而予以拒收；若d1=1，则抽取第二样组，n2=2n1，从n2中检测到的不合格品数为d2。如果d2=0，即d1+d2≤1，则认为该检验批为合格批而予以接受；如果d2＞0，即d1+d2≥2，则判定该检验批为不合格批而予以拒收。

例如，对于N分别为10000和500的检验批，采用复式抽验方案的OC曲线如图13-11所示。当P=3%时，对应于N=10000的L（P）=4.0%，而相对于N=500的L（P）=98.0%。由此可以看出：在P=3%条件下，如果以一万个产品作为一交付批时，只有4%的概率被接受，基本上不会被通过；如果把一万个产品分成20批，那每批500个产品，该交付批被接受的概率却高达98%，几乎是可以通过的。这同样也说明了百分比抽验的不合理性。

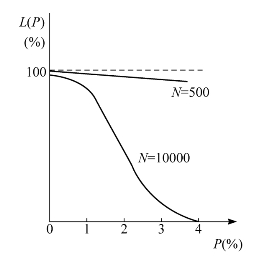
图13-11　复式抽验方案OC曲线（N=10000，500）

五、计数标准型抽验方案

（一）抽验中的常用参数

1.可接受的质量水平（AQL）　AQL是制订抽验方案的重要参数，它是抽验时认为检验批属合格批的批不合格品率（或每百个单位产品平均缺陷数）的上限值，即检验批作为合格批的最低质量指标。凡是P≤AQL的检验批都应该以高概率接受，以免给生产者造成过多损失，所以生产者比较关心AQL值。在制订方案时，应使方案的AQL值取在生产过程中长时期发生的平均过程不合格品率附近。AQL在数值上等于相应于α的批不合格品率P0。

2.批允许不合格品率（LTPD）　批允许不合格品率LTPD又称批的极限不合格品率或拒收的质量水平，是检验批被判为不合格批的批不合格品率的下限。凡是P≥LTPD的检验批都将被判为不合格批，而且以高概率拒收。该参数有利于对用户的利益进行保护，故用户对此参数比较关心。在制订单个孤立批或质量情况不明的检验批抽验方案时，此参数更显重要，其值相当于P1。

3.无差异的质量水平（IQL）　该参数可定义为当L（P）=0.5时的批不合格品率，IQL值介于AQL和LTPD之间。

此外，对于多批（大于10批）大量生产时的产品验收（非破坏性检验），还可使用平均出厂不合品率AOQ和平均出厂不合格品率极限AOQL等参数。

（二）计数标准型抽验方案的特点

计数标准型抽验方案属AQL型方案，此抽验方案同时控制两种风险，使对应于给定的AQL和LTPD的两种风险分别不大于给定的α值和β值，它对供需双方均可提供适当保护。计数标准型抽验方案的主要特点可归纳为以下几个方面。

（1）该方案通过选取相应于P0和P1的α值和β值（一般α=0.05，β=0.10），对使用者提供质量保证，对生产者保证其经济效益。

（2）该方案不要求生产者提供检验批诸如生产过程中的平均过程不合格品率或工序状态是否稳定等事前信息，故适用于使用者对每批产品质量要求较严的孤立批或市场上偶然成交的产品批的验收。

（3）对连续多批的产品验收，采用此方案的抽验量较大。

（4）该方案对破坏性检验和非破坏性检验均适用。

（三）P0和P1值的选定

在计数标准型抽验方案中，通常取α=0.05，β=0.10，它们都为某一确定值，而P0和P1如何选定是设计本方案的关键。P0和P1的取值并不是通过计算可以确定的，而是在抽验前由供需双方协商确定的。P0和P1的取值实际上是生产者与使用者之间平衡、妥协的结果，P0和P1的选定应考虑到以下几个因素。

（1）产品使用者应将可允许的批最大不合格品率定为P1，凡P≥P1的检验批均属不合格批，并希望以高概率拒收。当P=P1时，对该种质量水平检验批的接受概率希望控制在β=0.10左右。因此，产品使用者通过P1和β值而使产品质量基本得到保证。同时，产品生产者为了使具有一定质量水平的检验批不轻易被拒收，则提出一个可接受的质量水平P0，凡P≤P0时，该种质量水平的检验批被拒收的概率尽可能控制在α=0.05左右，并希望以高概率接受。

（2）P0值的选定要考虑到生产者的实际质量水平，即P0应与值相接近。对生产者来说，希望将P0值定得大一些，但P0值过大会影响生产者的质量声誉；对使用者来说，希望将P0值定得小一些，但P0值定得过小会加大生产者的质量风险，会使优质批被判为不合格批的概率增大。P1值的选定同样也必须充分考虑用户和生产者之间的利益。

（3）如果是根据产品缺陷的严重性进行分级的，P0值应取不同的标准：对于致命缺陷，P0值应取得小一些，如P0=0.1%、0.3%和0.5%等；对于轻微缺陷，由于造成的损失小，则P0值可适当取得大一些，如P0=3.5%或10%。

（4）P1值主要是根据使用者的质量要求确定的，对重要产品的P1值应取得大一些，选定P1值也要考虑到各种因素的影响，如果值过小，往往会使抽验量增大。

（5）从理论上讲，设计方案必须使，而实际中最好取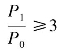。如果值过小会使抽取样组的n值过大而失去抽样检验的实际意义。如果值过大，会使β值增大而加大使用者的风险。通常，值为4～10为宜。

（6）在长期实践中，采用某抽验方案要使供需双方都比较满意，可采用反推法从某抽验方案的OC曲线上找出相应于1-α和β的P值，分别作为P0和P1值。在计算CP值的基础上，将估算出的P值作为P0的估计值。

（四）计数标准型抽验方案的设计

在一次抽验中，当P0、P1、α和β值选定以后，相应于P0的L（P0）=1-α，相应于P1的L（P1）=β，据此要求而可以得出设计所求的抽验方案（n/c）。在P0和P1值很小，且能够满足P＜0.1与nP为有限数的条件下，可以用泊松分布近似计算L（P）值，计算公式为：

结合公式可解出n和c。例如，对某产品进行验收时，设P0=1%，P1=10%，α=0.01，β=0.03，则

根据预先选定不同的c值，通过查阅泊松分布表，可以得到表13-2所示的计算结果。

表13-2　不同c值下的nP0和nP1值

因为本例的，所以从表13-2中查得项中c=3，相应的nP1=8.5，则，那么，所求方案为n=85，c=3。如果表13-2中没有与设定值完全相等的一项，则可以取较为接近的一项，此时按nP0和nP1计算所得的n值略有差异，但以n取大者为好，这对保证产品的质量有利。