一、分类法
分类法是指对每个检验对象判定为合格、不合格,或者是将检验对象分为若干等级的检验方法。例如,毛织物的手感要进行精细的定量分析是比较困难的,一般只分为1级、2级、3级、4级和5级五个级别,以此来区分毛织物所表现的不同的手感特性。针对分类法所采用的统计分析方法有管理图、二项概率纸、X2检验和科库兰Q检验法等,其中以科库兰Q检验法应用较广。下面结合实例就科库兰Q检验的方法原理及应用介绍如下。
表5-2给出的是10位检验员对13个产品样检验结果的分类情况统计表,从中可以看出:10位检验员对产品样6,8,9,10,11和12的判定一致性较好,且大多判为合格,极少有偏向性意见;对产品样4,5,7和13的判定一致性比较差,这主要是检验员A、B和C的评价结果不太一致所造成的;对产品样1,2和3,10位检验员评价结果的分歧最大。为了查出产生这种评价结果不一致的原因是由于随机原因,还是由于系统原因,必须把这种不一致的程度用数量表达出来,并用适当的标准加以评判。整个偏差的程度可以用科库兰Q值大小来表示,其计算公式为:
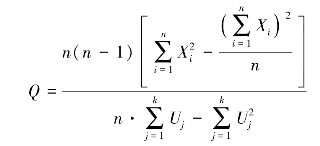
式中:n——检验员数目;
k——产品样数目;
X1,X2,…,Xi,…,Xn——各检验员判定的不合格数目;
U1,U2,…,Uj,…,Uk——各产品样被判为不合格的数目。
根据上式,并将表5-2中有关数据代入,
则

表5-2 10位检验员对13个产品样的检验结果

注 合格记“○”,不合格记“×”。
可以证明,统计量Q服从X2分布,其自由度为ν=n-1=10-1=9。所以,如给定显著性水平α=0.05时,X2(9,0.05)=16.92。
因为Q=31.7,X2(ν,α)=X2(9,0.05)=16.92,Q>X2(ν,α),所以,在显著性水平α=0.05时,经检验结果是有显著差异的,即各检验员对合格、不合格的判定有差异。虽然,用科库兰Q检验法可以检查出检验员对合格、不合格的判定差异情况,但是,用此方法还不能查出究竟是哪一位检验员的判定不当,这只能用其他方法进行调查,必要时对检验员加强训练和教育。
二、评分法
评分法是以评分方式对检验对象作质量特性判定,也称记分法。检验员记分可采用记分法和限定记分法两种不同的记分方法。如果记分有困难时,也可以采用比例尺(刻度尺)记分,如图5-3所示。图5-3所示的刻度尺采用在编排位置上作记号的方法。评分等级一般取3,5,7,10等,其统计分析方法可采用t检验和方差分析。

图5-3 刻度尺记分
三、顺位法
顺位法是将检验对象,根据其特定的标准作顺位排列的方法。通常,我们根据检验对象的质量优劣程度,从优至劣顺次记为1,2,3……针对顺位法所进行的统计分析方法主要有:威尔科克逊的U检验,克拉斯卡尔的H检验,斯比阿曼的顺位相关系数检验与顺位一致性系数,费利特曼的X2检验等。
(—)威尔科克逊(Wilcoxon)的U检验
【例题】为了比较两种不同上浆方案对某种织物经向强力的影响,对织物经向强力进行了试验,其部分实验结果如表5-3所示。根据表5-3的实验结果,按织物经向强力从高到低(从优到劣)作顺序排列,其结果如表5-4所示。对于A方案和B方案为同一顺位,表5-4中不予计入。问题是:根据表5-4的结果,能否判定出A方案和B方案对织物经向强力是否会造成差异?若有差异的话,何者为优?
表5-3 织物经向强力试验结果 单位:N

表5-4 织物经向强力顺序排列表

注 采用本方法时,A方案和B方案为同一顺位的,在本表中不予计入。例如表5-3中,A方案的360.6和B方案的360.6数值相等,为同一顺位,故未计入本表中。
解:
步骤一 找出方案A的顺位,本例为1,3,5,7,8,9,10,11,12,18;
步骤二 求出方案A的顺位之和∑Ri(统计量);
∑Ri=1+3+5+…+18=84
步骤三 根据下面给出的公式,求出双侧5%的界限值;

式中:m——方案A的样本容量;
n——方案B的样本容量。
本例m=10,n=10,查表得U0.025=1.96,
则

理论上可以证明:当样本容量足够大时,方案A的顺位和近似服从
 的分布。
的分布。
步骤四 统计结论,如果方法A的顺位和介于两界限值(79,131)之间,则表明方案A和方案B对所加工织物经向强力方面无显著影响,本例就属于这种情况。如果方案A的顺位和小于或等于下限值,则表明A和B两方案对织物经向强力有显著性影响,且A方案优于B方案。如果方案A的顺位和大于或等于上限值,则表明A和B两个方案对织物经向强力有显著性影响,且A方案不如B方案。
应用此方法要注意的是:采用本方法时,总的顺位是固定的,若方案A的顺位和已经求出,则B方案的顺位和同样也可以求得,如果用B方案顺位和证明,得到的结果是一致的;如果两种方案为同一顺位的,则在检验时不予计入。本方法对于连续变量的试验结果可以进行比较,而对于离散变量来说,本方法有一定缺陷,因为离散变量的数据重复性很强,过多的剔除数据会影响统计分析结果的可信程度。关于离散变量的统计分析方法,结合实例介绍如下:
【例题】某厂2026年12月上半月与2026年同期的18号精梳棉纱的棉结数资料列于表5-5中。试问:按表5-5提供的资料,检验A与B两个纱样是否属于同一总体?如果两者不属于同一总体,那么A与B两个纱样所属总体,在其质量上何者为优?
表5-5 棉结数

解:根据表5-5的试验结果,按棉结数由少至多顺序排列,则可以得到表5-6。分析表5-6给出的数据可以知道以下四项结论。
出现重复数据多,而且重复次数也多,这是离散型随机变量样本的基本特点。
表5-6中共有6个数据重复出现,即11、12、13、14、15和19这六个变值,我们称表5-6有六列重复数据,简称六列重复。
我们把数据重复出现的次数称为列长。例如,数据11共出现4次,则称11该列的列长为4;数据12共出现7次,则称12该列的列长为7;其他依此类推。
把A和B两个样本的棉结数据合在一起,按棉结数由少至多顺序排列,同时依次编号,此号即为秩数。秩数的计算方法如下:表5-6中的10因无重复,则秩数为1;11有4次重复,其列长为4,所以数据11的秩数为(2+3+4+5)/4=3.5;其他依此类推,本例的秩数表见表5-7。
表5-6 表5-5数据的顺序排列

表5-7 表5-6的秩数表

本例的计算和分析步骤如下:
(1)从表5-7中任取一个样本(一般取秩数较小的样本),计算其秩和数。本例取样本A,其秩和数TA为:
TA=1+3.5+3.5+…+19.5=124
(2)计算秩和临界值Ta。当样本容量大于4时,一般可以认为T的渐近分布是正态分布,该正态分布的参数可以用以下公式计算:

式中:m——样本A的容量;
n——样本B的容量;
N——样本总容量(N=m+n);
ti——i列列长;
r——样本中的重复列数。
本例中,m=13,n=13,N=26,r=6。
为了计算![]() ,应先计算出
,应先计算出 的值,这可以用列表方法计算,本例的计算可见表5-8。
的值,这可以用列表方法计算,本例的计算可见表5-8。
表5-8 重复的秩数、列长ti和![]()

将相应的数值代入T的正态参数计算公式中,可计算得到:
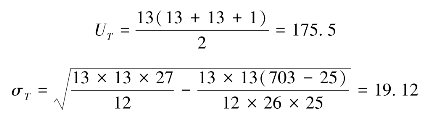 (https://www.daowen.com)
(https://www.daowen.com)
因此,在显著性水平α为0.05时,T的双侧临界值为:
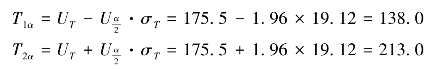
(3)统计结论。如果TA小于T1α,本例即为此种情况,则表明显著性水平α=0.05下,表5-4的两个样本不能认为同属一个总体,又由于TA小于Tα的下限,故可以推断:样本A所属的总体,其分布中心偏向左侧,其平均数是小于样本B的。根据本例的实际意义,则可以认为:2026年12月上半月生产的18号精梳棉纱的棉结数比2026年同期少,表明成纱质量有所提高。
如果TA大于T2α,则在显著性水平α=0.05下,表明这两个样本不属于同一总体,且由于TA大于Tα的上限,故可以推断:样本A所属的总体,其分布中心偏向右侧,其平均数大于B样本。
如果TA介于T1α和T2α之间,则在显著性水平α=0.05下,可以认为这两个样本同属一个总体,故可以推断:样本A的平均数与样本B相同。
(二)克拉斯卡尔(Kraskal)的H检验
【例题】梳理机用T15型盖板针布配以不同型号的锡林和道夫针布,纺出生条,经并合后制成熟条,其条干不匀率数据如表5-9所示。问题:这四种方案对熟条条干不匀率有无显著影响?
表5-9 熟条条干不匀率样本数据(由小至大排列)

解:
(1)将表5-9的全部数据混合在一起,并按数据由小至大的顺序编以秩号,分别计算各方案下的秩和数Ri,对不同方案内出现相同的数据,其秩数以相应的平均秩数代替。本例的结果列于表5-10之中。
表5-10 秩、秩和、秩和的平均值

(2)计算统计量H,H的计算公式为:

本例中,
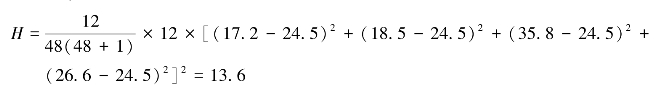
(3)统计结论。实践证明:在n>5,n·K>15的场合,统计量H近似服从X2分布,其自由度ν=k-1(k为方案数,本例k=4)。因此,在显著性水平α=0.05时,查表可得![]() 7.815,记H0.05=7.815;在显著性水平α=0.01时,查表可得
7.815,记H0.05=7.815;在显著性水平α=0.01时,查表可得![]() ,记H0.01=11.345。
,记H0.01=11.345。
由于H=13.6,H0.01=11.345,H>H0.01
故可以认为:在显著性水平α=0.01下,这四种方案有显著差异。根据本例的实际意义可以推断:用方案一制成的熟条条干不匀率最小,其质量最好,因为方案一的秩和数在这四个方案中最小。
(三)顺位一致性系数W和佛利德曼(Friedman)的检验
官能检验虽然具有直观、快速和简便等优点,但也带来一个问题,即对于同一检验对象,不同检验员的检验结果是否一致?这就产生了官能检验的检验一致性统计分析问题。当多位检验员对有两组以上样组作顺位评定时,必须要充分考虑所有数据的相关性,以便确定其间有无显著性差异。假定判别人员(检验员)为n人,被判别对象有k个,判别值为Rij,各组的判别顺位值之和为Tj,其关系列于表5-11之中。
表5-11 多检验员、多样组顺位评定中各项目的关系

顺位的不一致性可能是由于被判别对象的品质差异造成的,但也可能是由于判别员之间的分歧造成的。表征各判别员判定顺位一致性的统计量,经凯特尔研究可采用一致性系数W,其计算公式为:

W值一般在0与1之间。如果W值较小,则表明判定一致性较差,各判定对象之间的顺位均值的偏差较小;反之,如果W值较大,则表明判定一致性较好;如果完全一致,则W=1;如果一致性极差,则W趋于0。下面结合实例介绍此方法的应用。
【例题】选用五种不同密比(密比=纬密/经密)进行某种毛织物设计,制得成品后,由9名检验员对这五种毛织物作手感评定,其评定结果列于表5-12之中。问题:根据表5-12的数据,鉴别这9位检验员的手感检验是否有显著差异。如果没有显著差异,则可以根据表5-12所列的结果对这5种毛织物进行手感评定,同时也证明这9位检验人员可在不同地区或场合对该检验项目具有独立的手感评级能力。
表5-12 9位检验员对5种毛织物手感评定结果

续表

解:根据表5-12所列数据可知,n=9,k=5。

这里,W=0.694,由于W不等于1,说明这9位检验员的检验结果并不完全一致。因为官能检验本身具有随机性,即使是同一位检验员对同一对象作多次检验,其结果也非完全一致。那么,W的波动是由于检验员的随机原因造成的,还是检验员之间的系统原因造成的呢?这就要对W进行显著性检验。对W检验可分三种情况进行讨论。
第一种情况n和k都很大。对于这种情况,理论上可以证明,统计量W可按下面公式转换成统计量F:
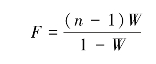
其自由度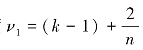 ,ν2=(n-1)ν1。若F>Fα,则在显著性水平α条件下,认为一致性良好;若F≤Fα,则在显著性水平α条件下,认为一致性很差。
,ν2=(n-1)ν1。若F>Fα,则在显著性水平α条件下,认为一致性良好;若F≤Fα,则在显著性水平α条件下,认为一致性很差。
第二种情况n和k都不是太大。此时,对W按如下公式进行修正:

然后再按第一种情况所述,将修正后的统计量W转换成统计量F,并进行检验。
第三种情况n和k都较小。在这种情况下,可以根据公式,直接把W中的分子S当作统计量,并按S的概率分布确定其临界值Sα。关于Sα值的确定方法这里不作介绍。若S>Sα,则在显著性水平α条件下,认为一致性良好;若S≤Sα,则在显著性水平α条件下,认为一致性很差。
就本例来看,n=9,k=5,属于第二种情况,那么:


统计量F的 ,取ν1=5;ν2=(n-1)×ν1=33.76,取ν2=34。查表可知,F0.05绝不超过2.69,F0.01绝不超过4.02。因此F=17.89的值远远超过F0.01的值。
,取ν1=5;ν2=(n-1)×ν1=33.76,取ν2=34。查表可知,F0.05绝不超过2.69,F0.01绝不超过4.02。因此F=17.89的值远远超过F0.01的值。
F统计结论:由于F远远大于F0.01,表明在显著性水平α=0.01条件下,这9位检验员的手感评级一致性良好。本例分析的目的,不仅仅是为了鉴定检验员的检验结果的一致性,而且在于确定不同密比毛织物的手感等级。为此,可以把表5-12整理成表5-13的形式。
表5-13 不同密比毛织物的手感等级

只有在一致性系数W(或S)得出一致性良好的结论以后,才可以根据Ti的大小去估计被评定对象的质量等级,其估计方法是:评定的等级顺位值与Tj的顺位值相对应。在本例中,Tj由小至大的排列顺序为13,19,29,30和44,则相应的手感等级分别为1,2,3,4和5级。
四、比较法
比较法是把检验对象每两个组成一组,并对每一组评定质量优劣的检验方法。例如,研究对象有A、B、C三种样品,其分组的组合为A和B、A和C及B和C,其统计分析方法可采用“封闭三角形个数法”。封闭三角形个数法也可称为成对比较法或配偶法等。下面结合实际例子介绍此方法的应用。
【例题】现有A、B、C、D、E、F和G共七种真丝双绉产品,这七种织物的经、纬密度相同,仅改变纬丝的捻度,捻度自0~600捻/米,每100捻/米为一档。由33位检验员对这七种真丝双绉的绉效应作官能评价,其中一位检验员的评定结果列于表5-14中,问题:该检验员是否具有识别能力?
解:表5-14中,每两种双绉样品配成一组,由检验员判定其优劣,并排列顺序。例如在A和B样组中,A优于B,则在表中A行B列交叉格中画符号“○”;在A和C样组中,A不如C,则在表中A行C列交叉格中画符号“×”,按此方法类推,就可以得到表5-14所列示的评定结果。为了鉴别该检验是否具有识别能力,评价其识别的可靠性,则进行如下处理:
表5-14 某检验员对七种真丝双绉的评定结果
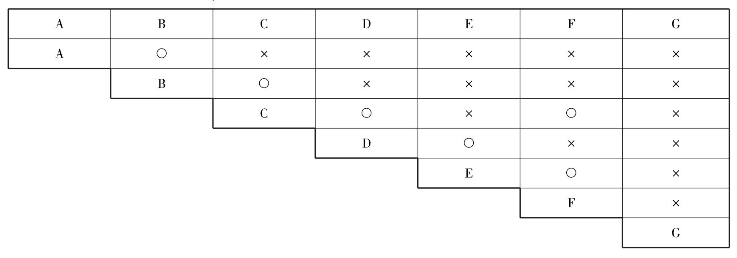

图5-4 封闭三角形
(1)作封闭三角形。首先把不同样品(本例样品数为7)分别置于圆周的不同位置,每个样品以平面上的一点按圆周等间隔分布,则每三个点可构成一个三角形,其间共能连接成![]() 个三角形。然后在样品之间捉对比较,并在两点之间的连线(即三角形的各边)上用箭头表示出表5-14的评定结果,该评定结果如图5-4所示。在A和B样组中,A优于B,则在A′B′连线上作“A′→B′”,或“B′←A′”(B不如A);在A和C样组中,A不如C,则在A′C′连线上作“A′←C′”,或“C′→A′”(C优于A);其他以此类推。
个三角形。然后在样品之间捉对比较,并在两点之间的连线(即三角形的各边)上用箭头表示出表5-14的评定结果,该评定结果如图5-4所示。在A和B样组中,A优于B,则在A′B′连线上作“A′→B′”,或“B′←A′”(B不如A);在A和C样组中,A不如C,则在A′C′连线上作“A′←C′”,或“C′→A′”(C优于A);其他以此类推。
由图5-4表示的结果可以看出:某些三角形的箭头首尾相接,将发生矛盾。例如,在△ABC中,A′→B′→C′→A′,由此循环,则无法判别出孰优孰劣。这种有矛盾的三角形被称为矛盾三角形或封闭三角形。本例出现5个矛盾三角形,它们分别是△A′B′C′、△B′C′D′、△C′D′E′、△D′E′F′和△B′C′F′。鉴别检验员有无识别能力可根据所发生的矛盾三角形个数来判定。
(2)求矛盾三角形个数。矛盾三角形的个数d可按下面公式计算:

式中,n——样本数;
ai——从各顶点向外引出的箭头数。
本例中,n=7,aA=1,aB=1,aC=3,aD=3,aE=4,aF=3,aG=6,则
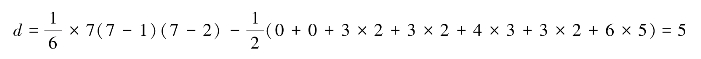
(3)检验。当n≤7时,可以用表5-15查得在显著性水平α=0.05时的界限值d0.05。如果d≤d0.05,则表明在显著性水平α=0.05条件下,检验员是有识别能力的,即检验员是能够判断出样品间的差异的。否则,如果d>d0.05,则说明在显著性水平α=0.05条件下,检验员缺乏识别能力。本例就属于这种情况,因为d=5,d0.05=3,d>d0.05,在此种情况下,可以让该检验员重新评定或请其他检验员来评定,在产生矛盾三角形处作重点研究。
当n>7时,应按公式 算出
算出![]() 值,式中
值,式中![]() 的自由度
的自由度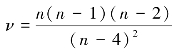 。如果
。如果![]() ,则表明在显著性水平α=0.05条件下,该检验员具有识别能力;否则,
,则表明在显著性水平α=0.05条件下,该检验员具有识别能力;否则,![]() ,则认为该检验员缺乏识别能力。
,则认为该检验员缺乏识别能力。
表5-15 n≤7,α=0.05时的临界值d0.05

秩位法(顺位法)和比较法在织物风格的官能评价方面应用较多,它们各有优缺点。采用秩位法可同时评价多种试样,可节省时间和人力,但试样数量过多会导致评定困难。采用成对比较法可以提高评定的精度,但耗时费力,如果试样数量为n块,则要检验n(n-1)/2次,考虑到检验人员的疲劳,成对比较法的试样数以8块为宜。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






