(一)遗传算法的含义

遗传算法是一类借鉴生物界的进化规律(适者生存、优胜劣汰遗传机制)演化而来的随机化搜索方法。它是由美国的J-tolland教授1975年首先提出,其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。遗传算法的这些性质已被广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。它是现代有关智能计算中的关键技术之一。

(二)遗传算法与自然选择

达尔文的自然选择学说是一种被广泛接受的生物进化学说,这种学说认为,生物要生存下去,就必须进行生存斗争。生存斗争包括种内斗争、种间斗争以及生物跟无机环境之间的斗争三个方面。在生存斗争中,具有有利变异的个体容易存活下来,并且有更多的机会将有利变异传给后代；具有不利变异的个体就容易被淘汰,产生后代的机会也少得多。因此,凡是在生存斗争中获胜的个体都是对环境适应性比较强的。达尔文把这种在生存斗争中适者生存、不适者淘汰的过程叫作自然选择。它表明,遗传和变异是决定生物进化的内在因素。自然界中的多种生物之所以能够适应环境而得以生存进化,是和遗传与变异生命现象分不开的。正是生物的这种遗传特性,使生物界的物种能够保持相对的稳定；而生物的变异特性,使生物个体产生新的性状,导致形成新的物种,推动了生物的进化和发展。

遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。它的思想源于生物遗传学和适者生存的自然规律,是具有“生存+检测”的迭代过程的搜索算法。遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。作为一种新的全局优化搜索算法,遗传算法以其简单通用、鲁棒性强、适于并行处理以及高效、实用等显著特点,在各个领域得到了广泛应用,取得了良好效果,并逐渐成为重要的智能算法之一。

(三)遗传算法的基本原理

长度为L的n个二进制串bi(i=1,2,…,n)组成了遗传算法的初解群,也称为初始群体。在每个串中,每个二进制位就是个体染色体的基因。根据进化术语,对群体执行的操作有三种。

1.选择(Selection)

这是从群体中选择出较适应环境的个体,这些选中的个体用于繁殖下一代,故有时也称这一操作为再生(Reproduction)。由于在选择用于繁殖下一代的个体时,是根据个体对环境的适应度而决定其繁殖量的,故而有时也称为非均匀再生(Differential Reproduction)。

2.交叉(Crossover)

这是在选中用于繁殖下一代的个体中,对两个不同的个体的相同位置的基因进行交换,从而产生新的个体。

3.变异(Mutation)

这是在选中的个体中,对个体中的某些基因执行异向转化。在串bi中,如果某位基因为1,产生变异时就是把它变成0。

(四)遗传算法的过程

遗传算法是从代表问题可能潜在的解集的一个种群(Population)开始的,而一个种群则由经过基因(Gene)编码的一定数目的个体(Individual)组成。每个个体实际上是染色体(Chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,往往需要进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(Generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(Fitness)大小选择(Selection)个体,并借助自然遗传学的遗传算子(Genetic Operators)进行组合交叉(Crossover)和变异(Mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应环境,末代种群中的最优个体经过解码(Decoding),可以作为问题近似最优解。

遗传算法的具体执行过程如图6-13所示。

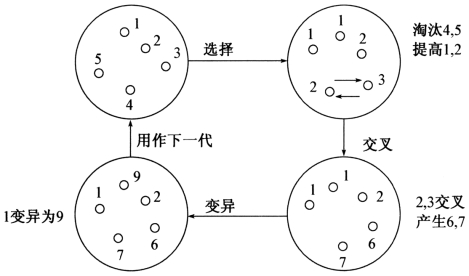
图6-13　遗传算法的执行过程示例

第一步,初始化

选择一个群体,即选择一个串或个体的集合bi,i=1,2,…,n。这个初始的群体也就是问题假设解的集合,一般取n=30～160。通常以随机方法产生串或个体的集合bi,i=1,2,…,n。问题的最优解将通过这些初始假设解进化而求出。

第二步,选择(www.daowen.com)

根据适者生存原则选择下一代的个体。在选择时,以适应度为选择原则。适应度准则体现了适者生存、不适应者淘汰的自然法则。

第三步,交叉

对于选中用于繁殖下一代的个体,随机地选择两个个体的相同位置,按交叉概率P,在选中的位置实行交换。这个过程反映了随机信息交换；目的在于产生新的基因组合,也即产生新的个体。交叉时,可实行单点交叉或多点交叉。例如有个体S1=100101,S2=010111,选择它们的左边3位进行交叉操作,则有S1=010101,S2=100111。

第四步,变异

根据生物遗传中基因变异的原理,以变异概率Pm对某些个体的某些位执行变异。在变异时,对执行变异的串的对应位求反,即把1变为0,把0变为1。变异概率Pm与生物变异极小的情况一致,所以,Pm的取值较小,一般取0.01～0.2。例如有个体S=101011,对其的第1、4位置的基因进行变异,则有S′=001111。

单靠变异不能在求解中得到好处。但是,它能保证算法过程不会产生无法进化的单一群体。因为在所有的个体一样时,交叉是无法产生新的个体的,这时只能靠变异产生新的个体。也就是说,变异增加了全局优化的特质。

第五步,全局最优收敛(Convergence to the global optimum)

当最优个体的适应度达到给定的阀值或者最优个体的适应度和群体适应度不再上升时,则算法的迭代过程收敛、算法结束。否则,用经过选择、交叉、变异所得到的新一代群体取代上一代群体,并返回到第2步即选择操作处继续循环执行。

(五)遗传算法的特点

遗传算法是解决搜索问题的一种通用算法,对于各种通用问题都可以使用。搜索算法的共同特征如下：

(1)组成一组候选解；

(2)依据某些适应性条件测算这些候选解的适应度；

(3)根据适应度保留某些候选解,放弃其他候选解；

(4)对保留的候选解进行某些操作,生成新的候选解。

在遗传算法中,上述几个特征以一种特殊的方式组合在一起：基于染色体群的并行搜索,带有猜测性质的选择操作、交换操作和突变操作。这种特殊的组合方式将遗传算法与其他搜索算法区别开来。遗传算法还具有以下几方面的特点。

(1)遗传算法从问题解的中集开始搜索,而不是从单个解开始。这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的,容易误入局部最优解；遗传算法从串集开始搜索,覆盖面大,利于全局择优。

(2)遗传算法求解时使用特定问题的信息极少,容易形成通用算法程序。

由于遗传算法使用适应值这一信息进行搜索,并不需要问题导数等与问题直接相关的信息。遗传算法只需适应值和串编码等通用信息,故几乎可处理任何问题。

(3)遗传算法有极强的容错能力。遗传算法的初始串集本身就带有大量与最优解甚远的信息,通过选择、交叉、变异操作能迅速排除与最优解相差极大的串,这是一个强烈的滤波过程,并且是一个并行滤波机制。因此,遗传算法有很高的容错能力。

(4)遗传算法中的选择、交叉和变异都是随机操作,而不是确定的精确规则。这说明遗传算法是采用随机方法进行最优解搜索,选择体现了向最优解迫近,交叉体现了最优解的产生,变异体现了全局最优解的覆盖。

(5)遗传算法具有隐含的并行性。