(一)聚类的含义

聚类分析是按照某种相近程度度量方法,将用户数据分成一系列有意义的子集合。每一个集合中的数据性质相近(即数据间的相似性尽可能大),不同集合之间的数据性质相差较大(即数据间的相似性尽可能小)。当要分析的数据缺乏描述信息,或者是无法组织成任何分类模式时,可以采用聚类分析。

聚类(Clustering)是指根据“物以类聚”的原理,将本身没有类别的样本聚集成不同的组(这样的一组数据对象的集合叫作簇),并且对每个簇进行描述的过程。它的目的是使得属于同一个簇的样本之间应该彼此相似,而不同簇的样本应该足够不相似。

图6-6是聚类算法的一种展示,图中的Cluster 1和Cluster 2分别代表聚类算法计算出的两类样本。打“+”号的是Cluster 1,而打“。”标记的是Cluster 2。

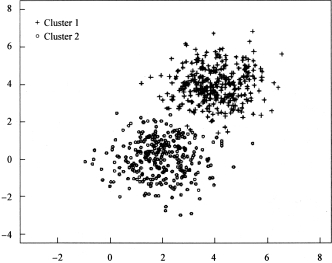
图6-6　聚类原理示意图

(二)聚类的特点

聚类问题不属于预测性的问题,它主要解决的是把一群对象划分成若干个组的问题,划分的依据是聚类问题的核心。(www.daowen.com)

和分类一样,聚类的目的也是把所有的对象分成不同的群组。与分类规则不同,进行聚类前并不知道将要划分成几个组和什么样的组,也不知道根据哪些空间区分规则来定义组。其目的旨在发现空间实体的属性间的函数关系,挖掘的知识用以属性名为变量的数学方程来表示。而且,在机器学习中,聚类是一种无指导学习。也就是说,聚类是在预先不知道欲划分类的情况下,根据信息相似度原则进行信息聚类的一种方法。

聚类问题容易与分类问题混淆,主要是语言表达的原因,因为常有这样的话：“根据客户的消费行为,把客户分成三个类,第一个类的主要特征是……”,实际上这是一个聚类问题,但是在表达上容易让人误解为这是个分类问题。分类问题与聚类问题是有本质区别的：分类问题是预测一个未知类别的用户属于哪个类别(相当于做单选题),而聚类问题是根据选定的指标,对一群用户进行划分(相当于做开放式的论述题),它不属于预测问题。

聚类的目的是使得属于同类别的对象之间的差别尽可能的小,而不同类别上的对象的差别尽可能的大。因此,聚类的意义就在于将观察到的内容组织成类分层结构,把类似的事物组织在一起。通过聚类,能够识别密集的和稀疏的区域,因而发现全局的分布模式以及数据属性之间的有趣的关系。

(三)聚类的应用

聚类分析广泛应用于商业、生物、地理、网络服务等多个领域,涉及数据挖掘、统计学、机器学习、空间数据库技术、生物学以及市场营销等多个学科,聚类分析已经成为数据挖掘研究领域中一个非常活跃的研究课题。在商业中,聚类可以帮助市场分析人员从消费者数据库中区分出不同的消费群体,并且概括出每一类消费者的消费模式或者消费习惯。它作为数据挖掘中的一个模块,可以做为一个单独的工具以发现数据库中分布的一些深层次的信息,或者把注意力放在某一个特定的类上以做进一步的分析并概括出每一类数据的特点。常见的聚类算法包括：K-均值聚类算法、K-中心点聚类算法、CLARANS、BIRCH、CLIQUE、DBSCAN等。

(四)聚类的实现

聚类的方法层出不穷,基于用户间彼此距离的长短来对用户进行聚类划分的方法依然是当前最流行的方法。大致的思路是这样的：首先确定选择哪些指标对用户进行聚类；然后在选择的指标上计算用户彼此的距离,距离的计算公式很多,最常用的就是直线距离(把选择的指标当作维度、用户在每个指标下都有相应的取值,可以看作多维空间中的一个点,用户彼此的距离就可理解为两者之间的直线距离)；最后聚类方法把彼此距离比较短的用户聚为一类,类与类之间的距离相对比较长。

聚类主要是以统计方法、机器学习、神经网络等方法为基础,比较有代表性的聚类技术是基于几何距离的聚类方法,如欧氏距离、曼哈坦距离、明考斯基距离等。