（一）Hotelling模型的基本框架

（1）在一个长度为1的线性城市中存在两家商店，它们提供的产品或服务是同质的；商店分别位于城市的两端，商店1位于x 1＝0处，商店2位于x 2＝1处，空间上的差异决定了两家商店的产品是有差异的；商店1和商店2的边际成本均为c1＝c2＝c，pi为商店i的价格，qi为需求函数，i＝1，2。

（2）消费者均匀地分布于城市的［0，1］区间内，可以用x∈［0，1］表示；消费者具有单位需求，即消费者只购买1个单位的产品；每个消费者购买单位产品所支付的交通成本记作t，则对于x∈［0，1］上任意一点x的某个消费者来说，购买商店1产品的交通成本为tx，购买商店2产品的交通成本为t（1-x）。因此，消费者向商店1购买的总成本为p 1＋tx，向商店2购买的总成本为p 2＋t（1-x）。

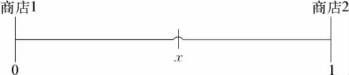
图5.6　Hotelling线性城市模型

现在考虑两家商店之间的定价竞争。假定两家商店同时选择自己的销售价格，如果住在x的消费者在两家商店之间购买是无差异的，那么，所有住在x左边的都将在商店1购买，而住在x右边的将在商店2购买。

为得到商店1和商店2的需求函数，考虑从两家商店购买无差异的消费者x（p 1，p 2），由p 1＋tx＝p 2＋t（1-x）可得：

因此，商店1和商店2的需求函数分别为：

商店的利润分别为：

由利润最大化一阶条件为零，可得：

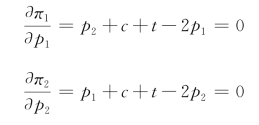
解上述两个一阶条件，得最优解为：

每个企业的均衡利润为：

由此，不难得到以下结论：Hotelling模型所分析的产品差异是由消费者所处的地理位置引起的。一定条件下，当交通成本t越高时，产品对于消费者来说差异性越大，厂商对市场就越有操纵力量，不同厂商出售的产品之间的替代性就会降低，借此厂商就可以制订较高的市场价格，获得高额的垄断利润。在特殊情况下，当交通成本为零时，商品被认为是无差异的。所以，任何一家商店的产品具有完全可替代性，两家商店也不可能将价格定在成本之上，最优价格等于成本，商店的最优利润为零。

（二）Hotelling模型的扩展

在以上分析中，假定两家商店分别位于城市的两端。为体现一般性，假设商店1距离左端点的距离为a，商店2距离右端点的距离为b，a＋b≤1（商店1位于商店2的左边，a＝b＝0与最大差异化相对应，a＋b＝1与最小差异化对应，即可完全替代）。如果商店位于这一区间内，则线性成本很难处理，因为一家商店把价格降到恰好能吸引住在两个企业之间的消费者时，它也能吸引住在对手另一边的所有消费者。而二次成本模型可以避开这个问题，为此，假定消费者的交通成本是二次非线性的，即消费者x∈［0，1］，若向商店1购买，交通成本为t（x-a）2。若向商店2购买，则交通成本为t（1-b-x）2，如图5.9所示。(www.daowen.com)

图5.7　二次线性成本扩展Hotelling模型

到两家商店购买无差异的消费者x（p 1，p 2）为以下方程的解：

解上式，得：

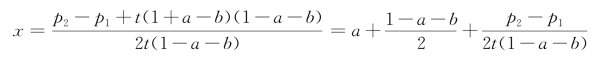
两家商店的需求函数分别是：

其中，q1与q2都是不大于1的非负数。分析式

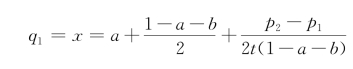
可以得到，在同一价格下，商店1控制着自己的领域，等于a。满足住在两家商店之间靠近1的半数消费者，数量为：，该式第三项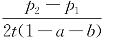：表示需求对价格差别的敏感程度。

商店1和商店2的利润函数分别为：

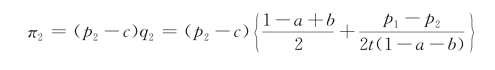
由一阶条件，得：

由此可得到以下结论：（1）当a＝b＝0，即商店分别位于两端时，＝＝c＋t，所得结论与基本模型结论一致；（2）当a＝1-b，即两家商店位于同一位置时，＝c。也就是说，如果两家商店是同质的，消费者只关心价格，竞争的结果是两家商店都不能获得超额利润。这一结论也表明，产品无差别会引起激烈的价格竞争，而产品差别化会弱化价格竞争。

（三）电子商务竞争平台Hotelling模型分析

目前对于电子商务领域竞争平台的研究还很少见。曹俊浩（2010）曾在其博士论文里研究了基于不同所有者结构的B2B电子商务平台的多平台竞争问题；李建平（2008）研究了移动数据增值业务平台中两个竞争平台的纵向关系问题；王维国（2013）研究了移动互联网平台的多平台竞争问题，从收益模式和服务差异化两个角度进行了讨论；李煜（2013）研究了双边多归属条件下的软件平台竞争模型；由于以上领域和电子商务平台的产业特征相近，因此，他们的研究也给本书提供了很好的借鉴。

参照Hotelling基本模型，假设竞争平台1两边的用户数分别为竞争平台2两边的用户数分别为。平台两边的用户效用分别为平台2两边的用户效用分别为。假设接入两个竞争电子商务平台客户端的用户数量总和是1，同时，平台商家端的用户总和也是1，即＝1，＝1。根据前面Hotelling模型的结论，可以推断出平台1和平台2两边的用户数：