（1）随机前沿生产函数模型

考虑到参数方法具有一定的经济理论基础，本书结合中国农牧户肉羊生产的实际情况，仍采用随机前沿生产函数分析法来测算肉羊生产的技术效率水平。其中，农牧户肉羊生产Translog随机前沿生产函数模型及其对应的技术效率损失模型表达式分别为：

其中，Yi表示第i个农牧户养殖的肉羊出栏活重；Xi和Xj表示第i和j个生产要素投入量；Ui表示第i个农牧户肉羊生产技术效率损失情况的非负随机变量，且Ui、Vi彼此相互独立；Zji表示第j个影响肉羊生产技术效率的解释变量。当βij的估计值均显著等于0时，（7-1）式就转化为C-D随机前沿生产函数：

（2）DEA成本效率模型

生产函数主要反映了生产过程中由一定的技术水平所决定的投入和产出之间的最佳组合和配置比例关系，却不能对这种组合或配置比例关系的经济利益情况进行全面完整的揭示和说明。但在肉羊生产活动中，养殖户追求的并非仅仅是投入要素数量最小化或产出数量最大化，而是追求经济利益最大化，因此，为了能够深入了解农牧户的肉羊生产行为，需要利用成本函数（或者收益函数和利润函数）来对农牧户肉羊生产过程中的经济效率进行深入的分析和探讨。通过实地调研了解到，农牧户的肉羊主要出售给当地的屠宰加工场或者活羊收购商贩，在活羊出栏过程中，农牧户议价定价能力较弱，基本上都是出栏活羊价格的接受者，活羊出栏价格主要受屠宰加工企业和收购商贩的需求、终端消费者对羊肉的消费需求、国际羊肉市场价格、政府政策等因素的影响。因此，基于成本最小化的行为假设，本研究对农牧户肉羊生产的成本效率（CE）及配置效率（AE）进行测算和分析，即研究农牧户在既定价格水平条件下是如何降低肉羊生产成本的。

成本效率模型最早是Kopp ＆ Diewert于1982年提出的。它反映出该决策单元与最优决策单元在控制成本方面的接近程度。在规模报酬不变（CRS）条件下，配置效率等于成本效率（CE）除以技术效率（TE），因此，通过测算调研地区样本农牧户肉羊生产的成本效率和技术效率便可以获得其配置效率（AE），即AE=CE/TE（Farrell，1957）。(www.daowen.com)

根据王建华（2011）的研究，DEA成本效率模型可定义如下：

在规模报酬不变的条件下，最小生产成本C*（P，Y0）可表示为：

由此可以得到最优解C*（P，Y0），则成本效率表示为：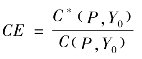

当CE=1时，说明生产要素投入有效，即生产成本达到最小化；当CE＜1时，生产处于无效的水平，说明实际投入成本过高。在实际生产过程中，决策单元通常处于规模报酬可变（VRS）的条件下，此时技术效率可分解为纯技术效率（Pure Technical Efficiency，简称PTE）和规模效率（Scale Efficiency，简称SE）。因此，可变规模报酬条件下的成本效率等于纯技术效率、规模效率和配置效率三者的乘积，即CE=PTE*SE*AE。