1.成本效率及其分解

根据经济效率的定义可知，在实际研究过程中，通过测算或估计得到的经济效率类型主要取决于采用的数据类型和基于先验性行为假设设定的函数形式（Coelli et al.，1998）。以生产函数为例，它主要反映了生产过程中由一定的技术水平所决定的投入和产出之间的最佳组合和配置比例关系，却不能对这种组合或配置比例关系的经济利益情况进行全面完整的揭示和说明。但在肉羊生产活动中，养殖主体通常追求的是经济利益最大化，因此，为了能够深入了解养殖主体的肉羊生产行为，需要利用成本函数（或者收益函数和利润函数）来对养殖主体肉羊生产过程中的经济效率进行分析。本研究将基于成本最小化的行为假设，对各地区养殖主体肉羊生产的成本效率（CE）及配置效率（AE）进行测算和分析，即研究各地区养殖主体在既定价格水平条件下如何降低肉羊生产成本，这在当前的情况下具有更大的现实意义。

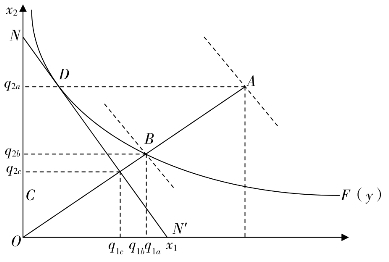
图6-2　成本无效率问题的分解情况

数据来源：Coelli et al.（1998）。

图6-2是Coelli et al.（1998）提出的基于两种生产要素x1和x2生产一种产出y的生产过程中成本无效率问题的分解图示，且已知生产要素x1的市场价格为p1和生产要素x2的市场价格为p2，由此可以得到肉羊生产主体的等成本线，即NN＇，F（y）表示肉羊生产主体的等产量曲线。从图中可以看出，当生产主体的生产位于A点即生产要素x1和x2的投入量分别为q1a和q2a时，对应的实际生产成本为C=p1q1a+p2q2a，此时最小成本为Cmin=p1q1c+p2q2c。从而可以获得生产主体肉羊生产的成本效率即最小生产成本与实际生产成本低的比率（Coelli et al.，2005），即

从图6-2不难看出，生产主体肉羊生产的技术效率（TEc）和配置效率（AEc）分别为：

根据数学计算公式变换可知：

式（6-8）表明生产主体肉羊生产的成本效率可以进一步分解为技术效率（TEc）和配置效率（AEc）两个部分，即CE=TEC*AEC。

2.随机前沿成本函数模型及其估计方法

同测算经济效率的方法类似，测算成本效率的成本前沿面分析方法也主要分为：基于线性规划分析的以数据包络分析为代表的非参数方法和以随机前沿成本函数模型为代表的参数方法。根据前面对两种方法的分析和比较可知，与非参数方法相比，参数方法在经济学理论意义、模型设定检验等方面具有更多优点。基于此，本书将采用随机前沿成本函数模型来测算和分析肉羊生产的成本效率，进而计算和分析其配置效率。多投入的成本前沿函数模型可以表示为：

其中，ci表示肉羊养殖主体的实际生产成本，C（p1i，p2i，…，pni，…，pNi；q1i，q2i，…，qmi，…，qMi）则定义了肉羊养殖主体在既定的技术水平条件下，在面对生产要素价格p1i，p2i，…，pni，…，pNi且产出分别为q1i，q2i，…，qmi，…，qMi时的最小生产成本（Coelli et al.，2005）。根据前面的分析以及成本前沿函数模型的表现形式可知，肉羊养殖主体生产的成本效率等于最小生产成本与实际生产成本的比值，即：

(www.daowen.com)

根据式（6-9）确定的成本前沿面实际上只是肉羊养殖主体生产成本的确定性部分，养殖主体生产成本还要受到很多不可控随机因素的影响。因此，在考虑不可控随机因素影响的情况下，肉羊养殖主体的随机成本前沿可以进一步表示为：

其中，确定性部分C（p1i，p2i，…，pni，…，pNi；q1i，q2i，…，qmi，…，qMi）对于各个养殖主体是一致的，反映不可控因素影响的exp（vi）对于各个养殖主体则存在差异，vi表示近似误差和其他统计噪声的对称随机前沿变量且服从正态分布N此时，养殖主体肉羊生产的成本效率为：

对于最小生产成本C（p1i，p2i，…，pni，…，pNi；q1i，q2i，…，qmi，…，qMi）*exp（vi）的具体设定形式，可以选择CD形式或超对数形式，其中CD随机成本前沿面被定义为（Schmidt，Lovell，1979）：

类似于对随机生产前沿面的分析，统计噪音只能部分地解释实际生产成本对最小生产成本或成本前沿面确定性部分的偏离，其他原因应归结为技术无效率和配置无效率引起的成本无效率（Coelli et al.，2005）。考虑到成本无效性的影响，由式（6-9）定义的C-D随机前沿成本函数模型可以等价地表示为：

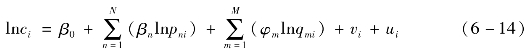
其中，ui表示非负的成本无效率变量，它服从半正态分布并且与vi相互独立。如果对于所有的n，当βn≥0并且满足：可以得到同质约束的C-D随机前沿成本函数模型，即：

对于超对数随机前沿成本函数模型的推导和C-D随机前沿成本函数模型类似。这两种随机前沿成本函数模型可以进一步简化为：

或者可以根据vi分布所具有的对称性表示为：

根据成本效率的定义，与随机前沿生产函数模型的估计类似，可以采用最大似然估计法对随机前沿成本函数模型进行估计，得到的成本效率或总经济效率可以表示为CEi=exp（-ui）。根据成本函数与生产函数之间所具有的对偶性以及成本效率和技术效率与配置效率相互之间存在的数量关系，可以进一步计算得到厂商生产的配置效率。

基于Frotier4.1软件，本书采用C-D随机前沿成本函数模型对中国各地区肉羊生产的成本效率进行最大似然估计，并在基础上进一步研究其配置效率及其影响因素，具体表达式为：

其中，cit表示第i个省（区）第t年的肉羊生产的总成本，已按各省价格指数统一折算成1999年的不变价格；p1it、p2it、p3it和p4it分别表示第i个省第t年的劳动力价格、仔畜（即羔羊）价格、精饲料价格和青粗饲料价格，qit表示第i个省第t年肉羊生产的主产品产量，T=1，2，…，19，为时间趋势变量；i和t同上；β为待估计参数；uit表示第i个省（区）肉羊生产成本效率损失情况的非负随机变量，且uit～iidN+vit～iidN（0，），uit、vit彼此相互独立。其中各要素投入价格均是通过对应的费用除以其投入量计算得到的。