（1）经济效率（Economic Efficiency，简称EE）。经济效率的概念最早是由Farrell（1957）提出的，他将经济效率分解为技术效率（Technical Efficiency，简称TE）和配置效率（Allocative Efficiency，简称AE）两部分。技术效率是指在既定的环境和技术条件下，生产者在既定投入下获得最大产出的能力，只有当一个生产者在投入既定的条件下能够实现产出的最大化时，才能说明该生产者是技术有效的，否则，就存在技术无效率；配置效率是指在既定的生产技术水平和价格下，生产者使用最佳投入要素比例的能力，如果一个生产者在现行的、既定的要素市场供求条件下，通过使用不同要素的数量比例而获得最大可能的净利润，那么他（它）就具有配置效率。一个经济决策单元如果同时具有配置效率和技术效率，那么它在经济上就是有效率的（Kalirajan ＆ Shand，1974）。

（2）生产率（Productivity）。生产率又可以称为“生产力”，指的是在生产过程中产出与投入的比率（李琮，2000）。早期的生产率主要指诸如劳动生产率、土地生产率、资本生产率等单要素生产率，而现代经济学中的生产率概念更为广泛，指的是全要素生产率（Total Factor Productivity，简称TFP），即除去劳动力、资本、土地等物质要素投入贡献之后的“余值”，这个“余值”包括效率的改善、技术进步以及规模效应，另外还包括没有识别（或者根本无法识别）的一些引起产量变化因素的作用（Denison，1974）。为了现阶段研究的需要和计算结果的进一步精确，通常将全要素生产率的变化归结为是由技术进步、纯技术效率、规模效率和综合技术效率的变化造成的。

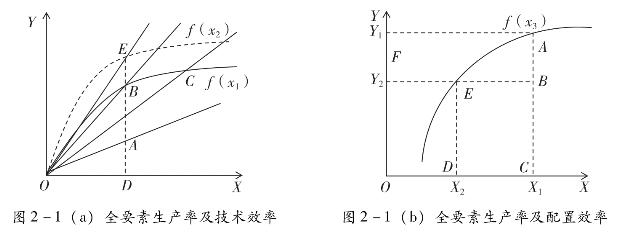
为更直观地理解肉羊生产技术效率、配置效率和全要素生产率的概念，本书以图2-1（a）和图2-1（b）做出说明，为进一步将问题简单化，只讨论一种投入和一种产出的情况。在图2-1（a）和图2-1（b）中，X轴代表某一种投入要素，Y轴代表相应的产出。f（x1）、f（x2）和f（x3）分别代表不同的生产前沿面，但都表示在现有的技术条件下，既定投入水平时产出能够达到的最优可能边界。当养殖主体在肉羊生产过程中存在效率损失（技术效率或者配置效率）时，肉羊的出栏活重或者养殖主体的净利润则位于生产前沿面内，如果生产前沿内的点距离前沿面越远，表明养殖主体肉羊生产的无效率水平越高。

(www.daowen.com)

图2-1　全要素生产率、技术效率和配置效率

在图2-1（a）中，A点、B点和E点的投入都是一样的，但产出却不相同。具体来看，在现有的技术水平下，A点在生产前沿面f（x1）以内，表示生产无效率点，而B点在生产前沿面f（x1）上，代表着生产有效率的点。两个点之间的距离代表技术效率损失的程度，距离越大，效率损失越多。随着时间的推移，肉羊的生产出现了技术进步，生产前沿面也随之上移，由原先的f（x1）上移到f（x2），即相同投入下可能的最大产出变大。此时，A点和B点都在新的生产前沿面f（x2）以内了，都是生产无效率点，而与A、B两点投入相同的E点此时在生产前沿面f（x2）上，为在出现了技术进步以后的新的生产有效率点，且A、B两点的技术效率分别为DA/DE和DB/DE。图2-1（a）中的全要素生产率即为从原点出发的射线的斜率。如果一个生产者从A点移到B点，斜率变大，意味着全要素生产率的提高，同时技术效率也得到了提高。从C点移到B点，技术效率不变，但是全要素生产率得到了提高。同样，随着技术的进步，生产者从B点移到E点，全要素生产率也会提高。另外，由图2-1（a）还可知，无论是技术效率提高还是技术进步，都会带来生产者全要素生产率的提高。如果技术进步的速度过快，可能同时伴随着技术效率的相对下降。

在图2-1（b）中，A点在生产前沿面f（x3）上，对应的要素投入量为X1，产出为Y1，但是可能会因为现实的生产技术水平低下或者规模不经济导致投入要素结构不合理等，使得实际的产出只能达到Y2，即B点的位置，此时投入要素的生产率为Y2/X1。若基于产出最大化考虑，最优产出应为Y1，然而，实际产出却只能达到Y2。由此可知，产出损失即为AB=|Y1-Y2|，此时的生产要素配置效率可以被表示为TE1=Y2/Y1=CB/CA=1-（BA/CA）；若基于投入最小化考虑，当实际产出为Y2时，如果不考虑外界效率损失的情况下，只需投入X2即可，即E点对应的位置。因此，B点存在明显的要素投入过量问题，所浪费的资源投入量为EB=|X1-X2|，此时生产要素配置效率可以被表示为TE2=X2/X1=FE/FB=1-（EB/FB）。