利用随机前沿生产函数评价技术创新效率的关键是投入产出指标的筛选。国内外学者在评价企业技术创新时，一般选择研发人数和研发费用作为投入指标。如冯根福、刘军虎等(2006)，刘云、杨湘浩(2012)选取研发经费作为资本支出指标，技术人员作为劳动支出指标。衡量技术创新产出的指标有许多，技术创新产出衡量指标较多，多以专利申请数和新产品营收为主，因销售收入统计口径和定义并不清晰，20世纪70年代后，专利数量成为技术创新产出的主要衡量指标。参考现有文献资料，本书生产函数的投入指标为企业当期的研发人员和费用，产出指标为当期申请专利数量。

参考朱有为等(2006)以及Coelli(1995)的模型，本书随机前沿生产函数模型为:(www.daowen.com)

其中，下标i和t分别表示企业和时间。Y、RD和RDP分别表示当期专利申请量、当期企业研发费用和研发人员。α和β分别代表企业研发费用和研发人员的产出弹性。b0表示待估常数项。Vit-Uit代表方程的随机误差项，具有复合结构。其中Vit指经济系统不可控因素冲击的噪声误差，假定其服从正态分布N(0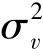，)，且独立于Uit。Uit为非负随机变量，考察研发活动中的技术无效率，假定其服从截尾正态分布N(Mit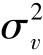，)。e-Mit用来表示企业i在t时期研发活动的技术效率，其数值越大说明技术效率越低，也就是说技术无效率程度越高，意味着等量投入研发费用和研发人员但获得的专利申请量却越少。