每个城市都有其各自的产业集聚模式，因此需要选用合适的特征来反映城市的产业集聚模式。

相关研究中，一般将专门化经济与多样化经济定为两个参数，但这并不符合两者的关系。因为，专门化经济与多样化经济并不是两种独立的事物，而是产业集聚模式某种特征的两个方面。更为符合逻辑的做法是，是将二者视为以产业份额来衡量产业集聚模式某种特征的正与负两种方向，以一个指标来代替，通常是选用绝对均衡数值法或相对均衡数值法。本书选用数值法中的Hi指数的改进形式作为衡量产业集聚模式的份额系数，详细算法见5.2.1节中的式（5-18）。

除了从产业份额来衡量产业集聚模式是专门化还是多样化，还需要从产业集聚的相关性和无关性的角度出发来衡量产业集聚模式的产业相关系数。虽然，有一些学者的研究中涉及这一方面，但根据本书3.4.2节及图3.5中的说明，很多研究对无关性和相关性处理的正确性还有待商榷。为了更加符合理论基础与现实情况，本书认为应该从5.1.3节的产业间关系法出发，依据产业间的投入产出关系，构建一个衡量城市内产业集聚的相关性与无关性的相关系数，计算方法见5.3节的式（5-19）。相关系数构造的理论依据是区域投入产出表衡量的区域内产业间的投入产出关系，两个产业在投入产出间关系越大，说明两个产业的关系更强。

衡量产业集聚中各产业间分布的专门化与多样性程度的份额系数，与衡量产业集聚中各产业间联系的相关性与无关性的相关系数，是产业集聚中集聚与分工的交互体现。在以往研究中，一般只关注产业集聚时不同产业的份额比例，强调产业内部的关系，而忽视了产业间的关系。本书认为，在考虑集聚系数的同时加入对相关系数的分析，能够更加符合现实中不同城市在产业集聚模式上存在的差异。

此外，对外开放程度也体现出一种城市与外部区域的关系，其对城市产业集聚模式与经济产出也有明显的影响，本书以城市正态分布标准化后的货运量来表示，以下简称开放系数。

综上所述，本书以份额系数、相关系数与开放系数来综合地评估一个城市的产业集聚模式特征。因此，分析一个城市产业集聚的形成机理，就要从城市的产业集聚模式的三个特征出发。(www.daowen.com)

首先，对于产业集聚模式的份额系数而言，根据7.1.3节所获结论，工业品生产规模、劳动力投入等因素对于专门化的产业集聚呈现负向作用，而这些因素都与城市规模正相关，因此可以假定城市规模的扩大会降低产业集聚的份额系数。另一方面，技术效率会使专门化的产业集聚呈现自增强作用，其会提升产业集聚的份额系数。

其次，对于产业集聚模式的相关系数而言，城市规模的扩张主要体现在其主要集聚产业的规模扩张上，而主要集聚产业的规模扩张将吸引相关产业的流入，从而形成相关性的产业集聚，因此可以假定城市规模的扩大会提高产业集聚的相关系数。

最后，对于产业集聚模式的开放系数而言，城市规模的扩张将扩大其产业原材料需求、产品销售，并延长其产业链的长度，这将促进城市的开放程度，因此可以假定城市规模的扩大会提高产业集聚的开放系数。

根据上述假定，本书以经济规模反映城市规模，因此构建产业集聚形成机理的3个解析模式分别为

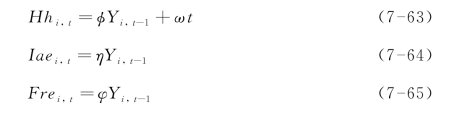
在式（7-63）—式（7-65）中，Hhi，t，Iaei，t与Frei，t分别为i城市第t年的份额系数、相关系数与开放系数。Yi，t-1为i城市第t-1年的产出；t是时间标量；ω用来衡量逐步增强的技术效率；φ，η，φ分别为Yi，t-1对Hhi，t，Iaei，t与Frei，t的影响系数；各参数预期的取值范围为φ≤0，ω≥0，η≥0，φ≥0。