产业地理集中现象测评的主体是单个产业，常见的评测方法有个别对象法、数值法、图示法、区域间关系法。其中，数值法依据方法构造的不同，又可以分为绝对均衡法、相对均衡法、组合法。这些方法的常见方法与指标举例及说明如表5.2所示。对产业地理集中现象的评测可从单个产业扩大至全部经济活动（产业），只需将单个产业的绩效指标xij替换为全部经济活动的绩效指标xi·。

表5.2　产业地理集中现象的评测方法及说明

1.个别对象法

个别对象法在考察产业地理集中现象时，并未考虑产业j在所有区域的分布情况，而只是重点考虑了个别区域（特别是对于产业j绩效较大的区域），常见的方法有城市首位律（Law of the Primate City）及各种城市指数。城市首位律由Jefferson（1939）提出，其在研究51个国家的前三位城市人口规模的比例关系时，发现最大城市与第二大城市的人口、经济、政治、社会、文化等各方面的绩效存在巨大差距，他将这种大城市“赢者通吃”的现象定义为城市首位律，并将最大城市定义为首位城市（Primate City）。后来，徐学强等（2009）、陈恩和谭小平（2009）、段七零（2011）、王蕊和范钦杰（2012）等学者先后采用2城市指数、3城市指数、4城市指数和11城市指数来衡量一个国家（或区域）前几位城市的绩效分布状况。可以发现，城市首位律及各种城市指数常见于经济地理研究中，因为不重视细分产业，在选择指标时，一些学者们常以xi·来代替xij，将对单个产业地理集中现象的研究上升至对全部经济活动地理集中的研究，但从方法的设计而言，城市首位律及各种城市指数是可以用于研究单个产业地理集中的，如陈恩和谭小平（2009）在研究中就计算了各行业的3城市指数。

城市首位律及各种城市指数虽然直观简便，但其致命的缺陷是只关注于绩效排名前几位区域的比例关系，而忽视了其他城市的绩效分布情况，难免有以偏概全之嫌。

2.绝对均衡数值法

数值法在构造评测产业地理集中现象的指标时，以整体区域的产业j的总绩效为参照系，一般是将xij除以x·j得到，然后根据对均衡不同的理解与评测基础，对进行不同的处理。

其中，绝对均衡法在评测每个产业的地理集中时，不涉及其他产业，是从绝对集中（Topographic Concentration）的视角出发（Bruhart，2005），以产业在所有区域的等比例分配作为绝对分散状态，并以此为参照系来评测特定产业j的地理集中水平。在指标构造时，绝对均衡法是直接以各个区域的来构造的。常见的绝对均衡法主要有碎化指数（CRj指数）、均匀度指数（UNIj）、OGj指数（Ogive Index）、赫芬达尔指数（Herfindahl Index，HIj指数）、熵指数（Entropy Index，ENj指数）以及位序-规模法则（Rank-Size Rule）中的分形数qj。

CRj指数由Wolfson（1994）提出，与城市首位律及各种城市指数相同，CRj指数常见于经济地理的分析中，一般用于整体绩效分布的分析，但也可以用于评测单一产业的分布现象。当用于单一产业分布的评测时，其指标形式即是各地区的平方根之和：

李小虎和张志斌（2011）修改了CRj指数，得出的碎化指数形式是的平方根之和：

OG指数由Tress（1938）提出用于测度区域的多样化，后被Bahl（1971），Hackbart（1975），Wasylenko（1978），Attaran（1987）用于测量区域的专门化，但通过对区域i与产业j标量的互换，OG也可以用于产业地理集中的评测。为了区别，评测产业地理集中称为OGj，评测区域产业集聚的称为OGi。OGj反映的是产业j在各区域比重与等比例分配1/m的差距，其指数形式为

当OGj指数为零时，说明产业j在各区域分布相等，产业集中程度最低，分散程度最高。OGj指数越大，则说明产业j在各区域分布越集中。

HIj指数则是直接对求平方和，其指数形式为

与OGj指数类似，HIj指数从小至大的变化反映出产业j在各区域分布的集中程度由弱变强，而分散程度则由强变弱。其实HIj指数可以由OGj指数线性变换得来：

OGj指数可视为Hij指数的线性变换形式（狄乾斌，2013）。

熵最初是由德国物理学家Clausius提出的热力学概念，被用于计算能量在空间中分布的均匀程度，后被广泛运用于生物学、信息论、概率论中（Shannon，1948）。Theil（1967）将其引入经济学分析中，用于收入分配的研究，因此熵指数又称泰尔（锡尔）熵指数（Cowell，1995）。20世纪70年代开始，以熵概念构造的ENj指数被用于区域经济分析（Hackbart，1975；Smith，1988；Aiginger，2004）。

在评测产业的地理集中时，ENj指数被用于研究产业在区域分布情况，其指数形式为

当产业j仅分布在一个区域时，ENj为零，此时产业j是完全集中的，而ENj越大，则说明产业j在区域间的分布越均匀。若将整体区域进行二次及以上的细分，ENj指数可以将产业地理集中分解各中间区域内的产业集中与各中间区域间的产业集中。

除了以为基础直接构造指标来评测产业地理集中的态势外，在经济地理、城市经济与城市规划研究领域，还有很多研究是以位序-规模法则与分形理论来开展的。分形理论（Fraetal Theory）是用来描述表面看来不规则却具有内在规律与自相似性（Self-Similarity）^[1]的空间形态或现象（Mandelbrot，1983）。Auerbach（1913），Lotka（1925），Singer（1936）等发现城市绩效分布的特征符合分形规律。城市（区域）的整体绩效xi·或某一产业的绩效xij与其位序指数的乘积为一个常数，经过线性变换后，其形式为

式（5-9）中，xij是整体区域内各细分区域按照j产业的绩效从大到小进行排序后第i位区域j产业的绩效；Rij是按照j产业排序的第i位城市位序，C为常数。通过对式（5-9）的估计，可以估算出j产业的qj，qj越大，j产业的地理分布越集中，qj越小，j产业的地理分布越分散（周彬学，2012）。

位序-规模法则被广泛地应用于国内外城市绩效分布规律的研究，一些学者对其提出了改进。如Rosen（1980）提出了规模-位序法则双对数关系的二次和三次形式。陈彦光（2004）提出了位序-规模的三参数模型。程开明和庄燕杰（2012）考虑了空间自相关性，构建了位序-规模法则的空间滞后模型。

3.相对均衡数值法

与绝对集中视角出发的绝对均衡法相比，相对均衡法在评测某个产业的地理集中现象时，是从相对集中（Relative Concentration）的视角出发（Bruhart，2005），以其他产业的地理分布为标准来评测。

绝对均衡法与相对均衡法的评测差别可以由图5.2说明，在运用绝对均衡法评测产业地理集中时，产业1与产业2均具有很强的地理集中现象，而运用相对均衡法评测产业地理集中时，产业1与产业2的各种指数均为零，即不存在产业集中现象。

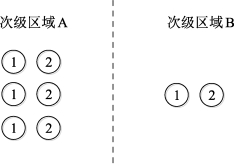
图5.2　产业地理集中绝对均衡法与相对均衡法的评测差别(www.daowen.com)

相对均衡法中，常见的指数有产业视角的区位（空间）基尼系数（Locational Gini Index，LGj指数）、赫希曼-赫芬达尔指数（Hirschman-Herfindahl Index，HHj指数）、全国平均指数（National Averages Index，NAj指数）、克鲁格曼相似指数（Krugman Similarity Index，SIj指数）、胡佛（Hoover）产业指数（HVj指数）、集中化指数（周一星，1986；成志芬，2007）与RAWLQj。

其中，HHj，NAj，SIj，HVj、集中化指数都与LGj指数（Marshall，1997；Krugman，1991）在思想与构造上有诸多相似之处，且可看做以单一产业实绩为计算指标的xij-xkj及以区域全部经济活动实绩为计算指标的xi·-xk·的区位基尼系数类似，只是绝对实绩与相对实绩、单一产业与全部经济活动的不同。这些函数均可被包涵在广义的LGj指数之下。这些指数在具体构造时的区别，其实只是对基尼系数的不同计算方法的区别。

一些研究中使用基尼平均差法（Gini'S Mean Difference Approach）来计算，指标的主体是的绝对值或平方和，反映的是某个产业地理分布与全部经济分布均值的差距之和（白重恩等，2004）。

如Hirschman对H指数的改进提出的HH指数，在用于分析产业地理集中，写为HHj指数，其指数形式为

而Bahl（1971），Dissart（2003）等人运用的NAj指数也可视为以各区域占全国经济活动比重bj的倒数对HH指数的修正，其形式为

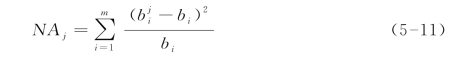
HHj指数、NAj指数都是以的平方和为基础构建，SIj指数、HVj指数则是以的绝对值为基础构建的。其形式分别为（Bernat Jr，2000；白重恩，2004）：

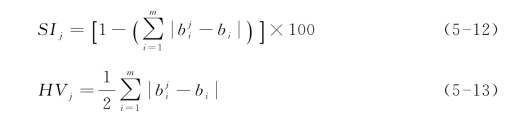
樊福卓（2007）文中的FIj指数即是HVj指数。

另一些研究中则使用协方差法（Covariance Approach）来计算，指标的主体是的绝对值或平方和，反映的是某个产业在两两区域间分布的差距。如赵继敏（2008）、张德常（2010）提出Gj指数的改进形式为

式（5-14）中，是区域k产业j的实绩占整体区域产业j的比重。

还有的研究中使用几何法（Geometric Approach），以区域个数（各区域按j产业的区位熵从小到大依次排序）为横轴，以产业j的区位熵累积数值为纵轴，计算洛伦兹曲线（Lorenz Curve）的围合面积，这其实是对上述数值法的几何图形体现（白重恩，2004；樊福卓，2007）。

另外，各研究中给出的系数也有差别，赵继敏（2008）将式（5-14）中的C设为n/2m2x，而张德常（2010）则将C设为n/4m（m-1）x。

除了Gj指数及相关指数外，还可以构造以区位熵为基础的产业地理集中评测指数。一般是将各区域j产业的LQij按照区域标量i加总，以反映j产业的分布情况。可将蒋媛媛（2011）提出的用以衡量区域产业集聚的RAWLQi进行更改，提出RAWLQj，指数形式为

Ellison（1997）从多个企业集聚概率的角度提出的EGγj指数，可视为一个组合型的指数，其形式为

可以看出，EGγj是由HIj与HHIj组成的，HIj与HHIj都是评测产业的地理集中现象的指标，因此EGγj也是用来评测产业的地理集中的，但是HIj为绝对均衡视角下衡量产业的地理集中的，即不考虑其他产业，而HHIj却是相对于其他区域来衡量产业地理集中的。由图5.2可以看出，二者在计算时可能会存在很大的差异，特别是对于全部经济活动集聚明显的中国。因此，某些学者认为EGγj具有内涵上的矛盾（樊福卓，2007）。

4.图示法

产业地理集中的评测还有图示法，包括无维度的饼状图、金字塔图与二维平面图、三维空间图。

无维度的饼状图、金字塔图在研究中的实用性不大，只能作为其他研究方法的补充。因为这些方法既不具备数值法中各种指标的标量性质（给出产业地理集中的标准）及进一步用于经验分析的作用，也不能将空间特征表现出来。二维平面图与三维空间图则可以将产业地理集中现象更为直观地表现出来。

二维平面图一般是运用各种图示方法将各产业在各区域的绩效分布运用密度地图表现，包括分级统计图法、等值线法、网格法等方法。分级统计图法、等值线法都是地理学中进行地图绘制的常用方法，其中分级统计图法是通过不同色级或不同疏密的晕线，来反映各产业的绩效在各区域的集中程度和分布差别；等值线法是运用绩效等值线表示绩效分布态势的渐变情况。陈述彭等（2002）认为等值线法由于假定绩效在区域内均匀分布，因此会掩盖实绩分布的真实性，他以“网格”作为中间载体，将卫星遥感像元与人口数据进行空间融合，将某一区域实绩（如县级制造业就业人口统计数据）分配到某一分辨率（如1 km栅格）的空间单元上。

三维空间图与二维平面图的本质差别不大，只是以峰度来反映二维平面图中以颜色、密度等来表示的区域绩效高低，因为具有三维空间的立体性，因此更加形象与直观。常见的有空间趋势面分析（Spatial Trend Surface Analysis，STSA），这种方法利用数学曲面来描述单个产业或全部经济活动的绩效在空间上的分布及变化趋势的方法。王伟（2009a，2009b）运用空间趋势面分析，对1995—2005年间的长三角、京津冀和珠三角经济空间的宏观形态进行了分析。

5.区域间关系法

数值法与二维平面图、三维空间图各具优势，数值法具备标量的可测度性并可以进一步进行经验分析，但数值法在构建指标时没有考虑区域间空间关系，因此在评测产业地理集中时可能与现实存在很大误差。通过图5.3中可以看出，在评测区域1与区域2某产业的地理集中现象时，因为区域1与区域2同样都在4个次级区域存在产业地理集中，而数值法在测算产业地理集中时将区域i视为同质的，不考虑其间的距离及其他关系，因此无论选用何种数值方法，计算出的两个区域的地理集中指数都是相同的。但是从实际情况出发，区域1的4个存在产业集中现象的次级区域，空间不具有临近性，而区域2的4个区域则是临近的。现实情况下，区域2的产业空间集中应该强于区域1。

图5.3　不考虑空间关系的数值法结论与现实不符

与数值法相比，二维平面图、三维空间图则可以将空间直观特征表现出来，但无法得出具体的数值，进行区域间与产业间对比，也不能进行进一步的经验分析。而区域间距离法则在一定程度上解决了数值法与图示法的矛盾，其在指标构建与分析时考虑了区域间的关系因素。常见的主要有SPj，Moran's I等指数。

SPj指数是由Krugman（1991）、Midelfart（2000）提出的，与一般数值法的指数相比，其考虑了区域间的距离。其形式为

式（5-17）中，uik为i区域与k区域间的距离，一般取区域的地理重心或j产业的绩效重心间的距离，常见的主要有直线距离、最近交通距离、时间距离与经济距离等。C为常数，黄新飞（2010）为将SPj指数控制在（0，1），取C为0.02。SPj指数越小，说明产业j在空间上越集中，反之，则越分散。

董青等（2010）、刘立平（2011）采用Geoda软件分别计算了1998—2007年5个年份的中国城市整体绩效分布的空间与局部Moran's I指数，Graham（2009）、贺灿飞（2011）提出了加入距离因素的市场潜力指数，也都是从空间的角度对产业地理集中进行分析研究。不过这些方法在运用时存在一些难点或不足，Moran's I指数需要借助空间分析软件，而市场潜力指数在指标设计中存在一些问题，以企业数量代替产值，并混淆了城市化与多样化经济（城市化经济）。