关于内生生育率下的人口增长，Becke et al.提供了一个迭代分析框架。［21］考虑到加总时可能出现的一些困难，巴罗和萨拉—伊—马丁建议在一个连续时间框架内对父母的生育行为进行分析，并据此构建了一个包含内生生育率特征的无限寿命家庭效用函数：［22］

其中，u（t）=u（xi（t），n（t））表示每个成年人的即期效用函数，xi表示产品i的消费量，n表示每个成年人生育的小孩数量。L（t）代表了t时的成年人数量，根据Becke et al.的设定，ε＞0，保证了利他性是孩子数量的递减函数。ρ表示主观贴现率。在式（1）中，主观贴现率的引入也反映了父母的利他主义程度。

代表性家庭由最初的一个成年人和他的后代组成。家庭向市场提供劳动和资产获得收入，并将所得用于消费、生育孩子和积累。拥有孩子能带给父母正的效用，并且这种效用随着孩子数量的增加是递减的。许多内生生育率文献都使用了柯布—道格拉斯类型的即期效用函数，这意味着孩子的数量为零时，再多的消费对父母都是无意义的。^[4]一个更为可取的假设是，尽管父母偏好于孩子的数量为正，但孩子并非是必需的。考虑到这些情况，我们给出的即期效用函数为：

这是对Dixit和Stiglitz（1977）分析产品多样化时使用的效用函数的一个扩展。其中，α和θ为决定孩子和其他产品替代弹性的参数。所不同的是，此处假设α＜θ，排除了孩子和消费的规模“报酬”不变和递增的特征。对于描述偏好的效用函数而言，这是一个更为真实的假设。况且，如若偏好不具有规模报酬递减的特征，在贴现率为正的情况下，家庭和个人更有激励在每一个时刻消费掉所有产出，长期分析有可能退化为一个静态问题。

在式（2）中，I=I（t）表示t时经济中的产品种类。通过式（2），我们可以对产品创新进行界定。简单地讲，产品创新导致I的增大。孩子和任一产品的消费都满足边际效用为正且递减的设定以及“稻田条件”，即当孩子或其他产品的数量趋于无穷大（或趋于0）时，其边际效用趋于0（或无穷大）。这些条件保证了父母偏好于多样化消费。因此，即便孩子并非是必需的，父母也会选择生育小孩。a和b的相对大小用来衡量孩子和消费的相对重要性，也反映了时代的特征，比如社会保障水平、要素市场的完善程度以及父母的价值观念等等。当a=0时，父母倾向于不要小孩。

k表示每个成年人拥有的资产。^[5]w表示工资率，r表示利率，E代表每个成年人的当期支出。假设资本的折旧率为零，式（3）和式（4）分别给出了家庭的动态预算约束方程和劳动人口的动态方程：^[6]

如果将式（2）直接代入式（1），并根据式（3）和式（4）构建汉密尔顿函数来求解这个动态问题，将面临两个控制变量和两个状态变量。再加上即期效用函数的加性特征，这将使得求解该问题变得异常复杂。过于复杂的求解过程和数学表达式极易掩饰相关的经济学含义。为了简化分析并得到直观的经济学解释，我们使用间接效用函数来代替式（2）。间接效用函数也有助于我们观察收入和价格（成本）变化时生育率和消费所发生的变化。

令E=cn+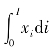，表示t时成年人的人均预算约束。其中，c表示生育一个小孩的成本，包括父母的时间投入和产品投入，并统一转化为产品进行度量。生育成本是时间的函数，随着技术创新而发生变化。在后面，我们将对生育成本与技术创新的关系进行讨论。根据式（2），家庭的最优生育水平和消费水平为：(www.daowen.com)

在上面的式子中，λ=（a/b）1/1-α，度量了孩子和消费的相对重要程度。当孩子的价格c上升时，父母选择减少小孩的数量而增加产品消费，支出水平的提高将引起生育率和消费水平的上升，这些都与标准的经济理论相一致。此外，式（5）和式（6）表明，产品种类的扩张将引起生育率和任一产品消费数量的下降。这是因为父母偏好于多样化消费，新产品的出现引起了支出的重新分配。定义：

并且，z1，z2通过c和I与时间相联系。据此有n=z1E，xi=z2E，并代入效用函数式（2），可得间接效用函数：

用式（9）替换式（2），由此得到无限寿命家庭效用函数：

其中，z（t）≡［az1（t）α+bI（t）z2（t）α］1/θ。将n=z1E代入动态预算方程式（3），有

此时，家庭的收入用于“支出”和积累，决策问题也同时由决定消费和生育率的时间路径演变为决定支出的最优时间路径的问题。根据式（10）、式（11）构建汉密尔顿方程：

横截条件为：=0。求解此动态问题可以得到：

其中，，分别表示每个成年人的人均有效支出水平和人均有效资本水平，并记-γA，根据式（13），可得：