1.指标体系的构建

根据前文中定义的经济增长质量，将其具体划分为经济效率、经济结构、经济运行及经济潜力四个评判维度。第一，经济效率维度。该维度主要测度经济增长过程中的投入产出关系。现有宏观经济研究中通常将投入要素分为资本、劳动和全要素，本文也试图从这三方面测度经济效率。其中，资本生产率和劳动生产率用来衡量资本、劳动单要素投入与产出之间的比率关系，全要素生产率用来测算所有结合投入要素与产出之间的比率关系。

第二，经济结构维度。本文重点考察反映经济增长质量的宏观结构，包括产业结构、需求结构、收入分配结构。此外，由于中国不但面临着所有国家和地区都会出现的区域经济不均衡，而且正处于从传统农业社会向现代工业社会转型的阶段，具有典型的二元经济结构特征。因此，将城乡二元经济结构和区域结构也纳入考量。在产业结构中，本文借鉴干春晖等（2011）的研究方法，采用第三产业产值与第二产业产值之比度量产业结构高级化，采用产业结构泰尔指数度量产业结构合理化。在需求结构中，采用投资率、消费率、投资消费比及居民政府消费比表征内需结构，外贸依存度则用来测度外需结构。需要指出，投资率、消费率指标并非越大越好或越小越好，而是应该控制在一个合适范围（贺铿，2006）。根据现有研究结果，本文将投资率和消费率的适度值分别设定为35%和60%。收入分配结构衡量国民收入在资本和劳动力要素之间的配置，采用劳动报酬占GDP比重度量。城乡二元经济结构通常采用二元对比系数、二元反差指数度量，本文再加入城市化率指标。区域经济差距通常采用区域差异系数与锡尔系数指标衡量，考虑到这两个指标的测算结果相似，本文只选取其一。此外，加入东西部人均收入比指标直接反映我国的区域差异。

第三，经济运行维度。宏观经济运行包括经济周期波动和系统性金融风险两方面。文献中对宏观经济周期波动的度量主要包括产出波动、价格波动和就业波动（钞小静等，2009）。遗憾的是，现有的权威就业数据统计并不完善，很多劳动力并未登记在册，因而这一数据并未反映真实的就业状况。考虑到无法获得实际失业率数据，本文放弃对就业波动的考察，仅从产出和价格两方面表征经济周期波动。产出波动指标选取经济增长波动系数和产出缺口，价格波动指标选取通货膨胀率和CPI指数。经济增长波动系数指标利用实际增长率与邻近五年的移动平均增长率间偏离度表示。系统性金融风险是潜在的经济波动因素。根据金融理论，金融风险通常包括利率风险、货币风险、信用风险、政策风险及国际收支风险。由于国家政策性金融风险不好度量，本文暂不考虑这一因素，仅从利率、货币及国际收支角度测度金融风险。利率风险测度指标选取存贷比，货币风险指标选取M2增速，国际收支风险指标选取经常项目赤字/GDP、外债/GDP。

第四，经济潜力维度。经济潜力维度衡量经济增长的可持续性，创新作为技术进步的源泉，被认为是经济持续增长的动力。因此，经济潜力维度包含制度创新和技术创新两个分项指标。制度创新用市场化指数代替，技术创新指标选取R&D强度、专利申请量、高技术产品出口额占GDP比重及国家科技拨款占国家公共财政支出比重来测度。市场化指数数据借鉴樊纲等（2011）、董晓宇等（2010）的研究成果。R&D强度指标缺失1990年以前的统计数据，考虑到长期以来政府财政科研支出是我国科研投入的主要形式，且通过将财政研发投入占GDP比重与R&D支出占GDP比重比较发现，两者的变动趋势相一致且数值相近，因此，1978—1990年的R&D强度由政府财政研发投入占GDP比重替代。

2.测度方法的选取

由于经济增长质量为多指标复合系统，因此，需要选择多指标综合评价方法将其合成为单一指数进行考察。多指标综合评价的核心在于指标权重的确定，赋权方法大体可分为主观赋权法（包括相对指数法、层次分析法等）和客观赋权法（包括熵值法、因子分析法、主成分分析法、投影寻踪模型等）两种。由于经济增长质量评价指标具有典型的高维、非线性特征，而传统多元分析方法建立在总体服从某种分布（如正态分布）的假定基础之上，实际中的数据往往不能满足该条件，因此需要用稳健的或非参数的方法解决，但“维数祸根”的存在使得非参数方法也很难奏效（李祚泳，1998）。

投影寻踪模型（Projection Pursuit Model，PPM），是由美国科学家Kruskal提出的一种用来分析和处理非线性非正态高维数据的新型数理统计方法，其基本思想是：将高维数据投影到低维子空间，寻找出能反映高维数据结构或特征的投影，在低维空间上对数据结构进行分析，以达到研究高维数据的目的。该方法的优点是对复杂高维数据变量的权重确定具有稳健性和客观合理性，能够克服传统多元统计分析方法基于正态分布的假设及处理高维数据稳健性差的缺陷。投影寻踪模型的构建思路是：通过建立以权重为优化变量的复杂非线性优化模型，将高维数据综合成以权重为投影方向的一维投影值（投影指标函数），在满足整体上投影点团之间尽可能分散而局部投影点尽可能密集的约束下，寻优获得目标函数最大化的最佳投影方向。投影寻踪模型成功的关键在于投影指标函数的优化，传统的优化方法是标准遗传算法（SGA）。但该算法在实际应用中存在早熟收敛、全局优化速度慢和解的精度差等缺点（金菊良等，2000）。基于实数编码的加速遗传算法（RAGA）在实现投影寻踪模型的过程中，克服了传统优化算法的弊端。因此，本文采用基于实数编码遗传算法的投影寻踪模型（PPM-RAGA）对1978—2016年中国经济增长质量进行测度。PPM-RAGA模型的构建步骤如下：

第一，评价指标的归一化处理。设各指标值的样本集为｛x*（i，j）|i=1～n，j=1～p｝，其中，x*（i，j）为第i个样本的第j个指标值，n为样本个数，p为指标个数。为消除各指标量纲效应，采用均值化方法对指标进行归一化处理：x（i，j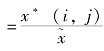），式中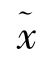，为第j个指标的平均值。

第二，投影目标函数f（a）的构造。PP方法就是将样本i的p维数据｛x*（i，j）|j=1～p｝综合成以a=｛a（1），a（2），a（3），…，a（p）｝为投影方向向量的一维投影值Z（i）：

优化投影指标时，要求投影值Z（i）尽可能多地提取x（i，j）中的变异信息，即Z（i）的标准差尽可能大，同时Z（i）的局部密度达到最大。投影目标函数可设置为：f（a）=SZDZ

式中，SZ为投影值Z（i）的标准差，DZ为投影值Z（i）的局部密度，即：(www.daowen.com)

式中，E（z）为序列Z（i）的平均值，R为局部密度的窗口半径，R的值可以根据试验来确定，一般可取0.1SZ，r（i，j）=|Z（i）-Z（j）|表示样本之间的距离，符号函数u（R-r（i，j））为单位阶跃函数，当R≥r（i，j）时函数值取1，否则取0。

第三，投影目标函数的优化。当各指标值的样本集给定时，投影目标函数f（a）只随投影方向而变化，不同的投影方向反映不同的数据结构特征，最佳投影方向是最大可能暴露高维数据某类结构特征的投影方向，因此，可以通过投影目标函数的最优化求解来计算最佳投影方向，即：

由于传统的优化方法难以解决a（j）为优化变量的复杂非线性优化问题，本文采用基于实数编码的加速遗传算法来实现高维全局寻优。

本文所采用的原始数据来源于《新中国六十年统计资料汇编》《中国统计年鉴》《中国科技统计年鉴》《中国国内生产总值历史核算资料（1952—2004）》《中国能源统计年鉴》《中国环境统计年鉴》及国家统计局网站数据库和世界银行数据库。基于PPM-RAGA模型确定的中国经济增长质量的基础指标及维度指数的权重见表2。

表2　经济增长质量指标体系

续表

由中国经济增长质量基础指标和维度权重可知，经济效率维度权重最高为0.734，经济结构维度的权重次之，为0.533。表明在1978—2016年间中国经济增长质量的变动更多体现在经济效率和经济结构两个维度变化上。经济运行和经济潜力维度权重相对较小，分别为0.223和0.357，表明这两个维度对经济增长质量的贡献度相对较小。

3.经济增长质量指数变动趋势

图1　1978—2016年中国经济增长质量各维度变动趋势

1978—2016年中国经济增长质量指数变动趋势如图1所示。总体上，经济增长质量四个维度的变动趋势呈现较大差异，中国经济增长质量是在四个维度的复杂相互作用贡献下，由低级向高级不断波动演进的。1978年以来中国经济增长质量总体呈波动上升态势，经济增长质量指数由1978年的1.16上升至2016年的2.532，上升幅度接近1.4。从具体维度来看，经济效率、经济运行和经济潜力均在波动中上升。其中，经济效率维度的波动幅度最大、上升幅度最小，总指数仅从1978年的1.668上升至2016年的2.024，上升0.3左右。经济运行维度在经历小段时间的波动下降后便开始不断上升，1978年经济运行维度指数为1.674，1988年下降至最低点0.858，随后便一直波动上升至2016年的2.316。经济潜力维度指数呈稳步上升趋势，从1978年的0.97显著提高至2016年的2.859，上升幅度1.9为四个维度中增幅最大的。四个维度中只有经济结构维度指数呈波动下降态势，从1978年的2.247下降至2016年的1.15，下降幅度超过1.0。