命题6-1的证明:

将零售商的反应函数F-（q 0）＝w 0erfT代入供应商的目标函数式（6-4）中，得到：

对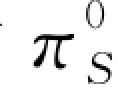（q 0）关于q 0分别求一阶和二阶导数可得：

因此，最优的订货量为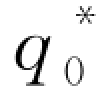＝qN，对应的最优批发价为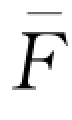＝（qN）e-rfT。

接着，简化银行的收支平衡条件，即式（6-2），得到：

引理6-1的证明:

注意到y 1＝（w 1q 1-b R）er1（L+T）＜q 1，因此

min{S（q 1），（w 1q 1-b R）er1（L+T）}＝min{X，y 1}

考虑到，因此式（6-8）显然成立。

命题6-2的证明:

首先，将式（6-9）代入式（6-10）中可得：

对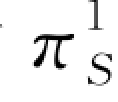（q 1）关于q 1分别求一阶和二阶导数可得：

其次，结合引理6-1可得：

推论6-1的证明:

当零售商在t∈（0，L）时刻预付款时，具体的决策时序变为：供应商在0时刻以贷款利率r S向银行融资生产成本；在t∈（0，L]时刻，零售商以贷款利率r t向银行融资并提前支付供应商的货款，供应商收到零售商的预付货款后偿还银行贷款；在L+T时刻销售结束，零售商偿还银行贷款。零售商的最优化问题为：

供应商的最优化问题为：

引理6-2的证明:

同引理6-1的证明，略。

命题6-3的证明:

对零售商的反应函数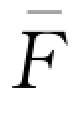（q 2）＝w 2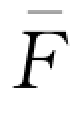（Y 2）两边关于w 2求导可得：

这里Y 2＝w 2q 2-b Rerf（L+T）。表达式（6-34）等价于：

即

进而可得：(www.daowen.com)

推论6-2的证明:

推论6-3的证明:

由推论6-2易得，略。

命题6-4的证明:

命题6-5的证明:

见正文，略。

引理6-3的证明:

对于约束条件式（6-21）中的（w 3q 3-b R）erf（L+T）＝E{min[S（q 3）+T（X），（w 3q 3-b R）er3（L+T）]}，其可简化为：

对式（6-38）关于q 3和w 3分别求导，得到：

以及

另一方面，零售商的期望利润表达式（6-20）等价于：

对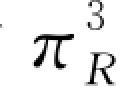（q 3）关于q 3求导并利用一阶必要条件可得：

对表达式（6-39）关于w 3求导可得：

g（y 3）w 3erf（L+T），因此V（q 3，y 3，δ，w 3）＞0。考虑到：

命题6-6的证明:

根据式（6-28），对π3S（w 3）关于w 3求导可得：结合表达式（6-40），并利用一阶必要条件则有：

推论6-4的证明:

令δ＝1，则对应的最优决策[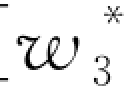（1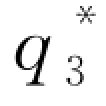），（1）]由下列方程组确定：

根据表达式（6-17）并结合引理6-2，可得：

另外，根据表达式（6-28）得：

即