在订货阶段，有三种情形：①两个零售商都提供资金补贴；②只有一个零售商提供资金补贴；③两个零售商都不提供资金补贴。记S表示提供资金补贴，N表示不进行资金补贴，为方便起见，可以用（X 1，X 2），X 1或X 2＝S，N表示这三种情形，即（S，S）表示零售商R 1和R 2都补贴，（S，N）表示零售商R 1补贴而零售商R 2不补贴，（N，N）表示零售商R 1和R 2都不补贴。

情形1：两个零售商都不进行资金补贴（N N情形）。

如果两个零售商都不进行资金补贴，零售商R i（i＝1，2）能够获得的最大订货量为B/2c。因此，零售商R i（i＝1，2）在第二阶段的最优化问题为：

在式（5-14）中，q i≤B/2c表示产能约束条件。由于R 1和R 2未对供应商进行资金补贴，因此两者的订货量不会超过B/2c，求解式（5-14），可以得到如下命题。

命题5-4.当两个零售商都不对供应商进行资金补贴时，第二阶段的均衡订货量为：

由于两个零售商进行古诺竞争，当二者都不进行资金补贴时，利用对称性，二者的均衡订货量是相同的。具体而言，当市场需求的实现值比较低时，供应商的资金水平可以满足零售商的订货量，此时第二阶段的均衡订货量为无资金约束时的均衡订货量，即为经典的古诺竞争均衡解。然而，当市场需求的实现值比较高时，供应商发生资金约束，只能对两个零售商均衡分配产能，这导致了两个零售商采购的数量不能满足市场需求。由此可见，零售商选择资金补贴是为了规避市场需求量较大，而供应商的资金水平比较低不能满足采购需求的风险。

情形2：只有零售商R 1进行资金补贴（SN情形）。

根据前面的假设，此种情形下R 1的单位采购成本为w，R 2的单位采购成本为w 0。不难写出R 1在第二阶段的最优化问题：

以及R 2在第二阶段的最优化问题：

参照Qi等（2015）的假设，本书假设补贴者对补贴额有绝对优先使用权。具体而言，零售商R 1补贴供应商ϕ1后，供应商的产能增加到（B+）/c，对于这部分产能，零售商R 1和R 2各自拥有B/2c的基本使用权；针对因补贴而增加的产能/c，供应商优先满足补贴者R 1的需求，因此R 1的总使用额可达到（B+2）/2c，而R 2能使用的最大额度仅为（B+）/c-q 1。(www.daowen.com)

这种优先满足补贴者的分配机制是为了保证补贴者有动力进行资金补贴。但是，考虑到剩余产能会被供应商用来服务竞争对手，即资金补贴的溢出效应，因此补贴者不会对供应商进行过度补贴。类似于情形1，可以得到两个零售商在第二阶段的均衡订货量依赖于具体的市场需求实现值。

命题5-5.给定市场规模α以及零售商R 1的资金补贴额ϕ1，第二阶段的均衡订货量满足：

值得注意的是，命题5-5中有一个潜在的假设：Φ/c+w＞w 0，即w 0-w＜Φ/c，这个假设意味着针对补贴的批发价优惠被限制在一定范围之内。当批发价优惠力度超过临界值Φ/c时，零售商R 1有动机对供应商进行大额度补贴，此种情形下均衡订货量为经典的古诺竞争订货量[（α-2w+w 0）/3，（α-2w 0+w）/3]。

命题5-5表明，在只有一个零售商选择进行资金补贴的情形下，当市场需求量适中的时候，会出现不对称的均衡订货量，进行资金补贴的一方获得较大订货量从而得到更多利润。基于此，竞争者也有可能选择补贴，以弥补订货不能被满足的困境。

情形3：两个零售商都进行资金补贴（SS情形）。

假设R 1和R 2分别向供应商补贴和，通常假设ϕ≥ϕ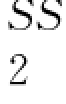，因此如果R 1无法达到最优化采购，R 2也一定无法达到最优化采购，反之不一定成立，二者的期望利润如下：

以及

命题5-6.给定市场规模α以及零售商R 1和R 2的资金补贴额（ϕ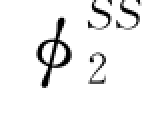，），如果两个零售商都选择资金补贴，则第二阶段的均衡订货量满足：

由命题5-6可以发现，即便两个零售商都选择资金补贴，还是存在不对称均衡。当市场需求不是很大时，补贴量多的一方会获得较多的采购量，从而获得更大的收益。考虑到这一点，两个零售商会基于补贴量进行博弈，博弈的结果就是两者的补贴量会相等。换而言之，如果两个零售商都选择补贴供应商，则最优的补贴额度必相等，否则至少有一个零售商偏离原有的补贴均衡。