引理4-1的证明:

当零售商无资金约束时，其期望利润表达式可写为：

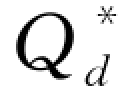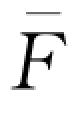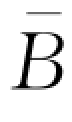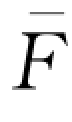容易得到此种情况下零售商的最优订货量为＝-1（w）。对应地，零售商获得无资金约束下的最优订货量所需要的最低资金水平＝w -1（w）。当零售商有资金约束，同时选择部分延期付款时，其期望利润表达式为：

这里y d＝（wQd-B）（1+r d），给定贷款利率r d，对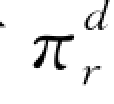（Qd）关于Qd求导并利用一阶必要条件可得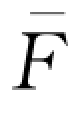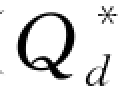（）＝w（1+r d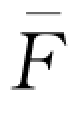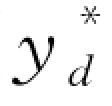）（）。特别地，当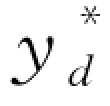＝0，即对应的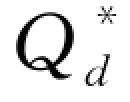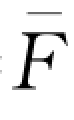＝-1[w（1+r d）]时，零售商仅使用自有资金无须延期付款，因此零售商选择延期付款模式所需的最高资金水平为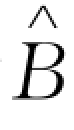（r d）＝w 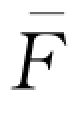-1[w（1+r d）]。当B＜（r d）时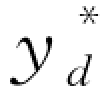，＞0，零售商选择延期付款；当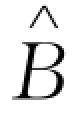（r d）≤B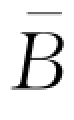＜时，零售商仅使用自有资金进行订货；当B≥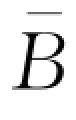时，零售商不受资金约束。

命题4-1的证明:

根据引理4-1，当零售商选择延期付款策略时，零售商的订货量满足：

考虑到y d＝（wQd-B）（1+Qd），因此式（4-36）等价于：

对式（4-37）两边关于y d求导，经过整理我们有：

另一方面，供应商的目标函数可简化为：

对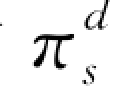（y d）关于y d求导，得到：

进一步结合式（4-38）并利用一阶必要条件，我们可得y d与Qd满足下式：

考虑到（wQd-B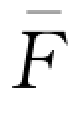）（Qd）＝wy d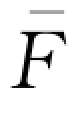（y d），上式可简化为：

因此，在不考虑供应商的下侧风险约束下，供应商和零售商的最优决策由式（4-7）确定。然而，当零售商的融资规模受到供应商的下侧风险约束，即约束条件（4-6）是紧的，供应商的最优信贷规模必在边界线y d＝α+F-1（β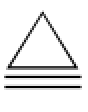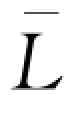）上取得，从而基于引理4-1，此时零售商的最优订货量必满足（wQd-B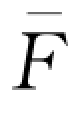）（Qd）＝w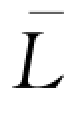 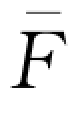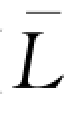（）。注意到方程（wQd-B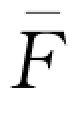）（Qd）＝w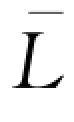 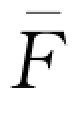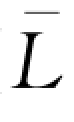（）有两个解，同时零售商没有动机订购过量的产品，否则订货成本将大大增加，因此最优的订货量为方程（wQd-B）（Qd）＝w 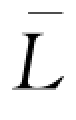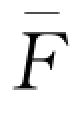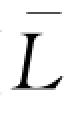（）较小的解。

引理4-2的证明:

首先，银行收支平衡约束条件式（4-1 6）等价于：

结合式（4-39）以及[u-v]+＝u-min{u，v}对于任意的u，v∈R总成立，因此零售商的目标函数可简化为：

对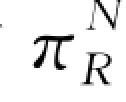（q 0）关于q 0求导，并利用一阶必要条件，可得无下侧风险约束下零售商的最优订货量为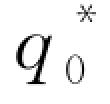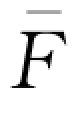＝-1（w）；另一方面，考虑银行的下侧风险约束：

命题4-3的证明:(www.daowen.com)

引理4-3的证明:

基于保险公司的补偿原则R 1＝[d 1-min（X，q 1）]+，因此可得：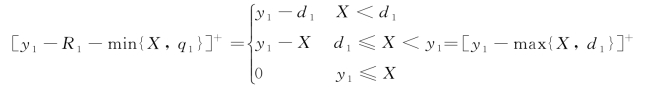

银行融资与保险混合模型中银行的下侧风险约束等价于：

Pro{[y 1-R 1-min{X，q 1}]+≥α}

＝Pro{[y 1-max{X，d 1}]+≥α}

＝Pro{y 1-d 1≥α|X＜d 1}F（d 1）+Pro{y 1-X≥α|X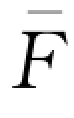≥d 1}（d 1）

基于上式，容易得到当d 1＜y 1-α时，Pro{[y 1-R 1-min{X，q 1}]+≥α}等价于F（d 1）+F（y 1-α）-F（d 1）＝F（y 1-α）；当y 1-α≤d 1≤y 1时，Pro{[y 1-R 1-min{X，q 1}]+≥α}＝0。

命题4-4的证明:

（1）由引理4-3发现，如果零售商购买信用保险，则其投保水平满足d 1＝y 1-α。由此，零售商的期望利润表达式可简化为：

根据式（4-20）和式（4-22），我们有：

注意到，F（x）dx以及min{X，y 1-R 1}＝min{X，y 1}，因此式（4-40）等价于：

对式（4-41）两端关于q 1求导，可得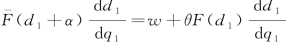，进而得到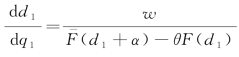。另一方面，对关于q 1求偏导，并利用一阶导数等于零的条件，容易得出：

（2）类似于命题4-3的证明，略。

（3）对式（4-41）和式（4-42）两端分别关于B求偏导，得到：

引理4-4与命题4-5的证明参见命题4-4的证明。