其中,y 1 (wq 1-B+P)(1+r 1)表示保险机制下零售商需向银行偿还的本息和。R 1=[d 1-min(X,q 1)]+表示零售商破产后,保险公司补偿给银行的金额。约束条件式(4-22)为基于期望保费原理的保险定价策略,其中θE(R)表示保险公司对保单承担的各种费用,主要包括:销售费用、税收、行政管理费用、利润和意外费用。特别地,当θ=0时,约束条件式(4-22)说明保险公司处于完全竞争的保险市场中,零售商所交的保费仅用来补偿损失:
(wq 1-B+P)(1+r 1)表示保险机制下零售商需向银行偿还的本息和。R 1=[d 1-min(X,q 1)]+表示零售商破产后,保险公司补偿给银行的金额。约束条件式(4-22)为基于期望保费原理的保险定价策略,其中θE(R)表示保险公司对保单承担的各种费用,主要包括:销售费用、税收、行政管理费用、利润和意外费用。特别地,当θ=0时,约束条件式(4-22)说明保险公司处于完全竞争的保险市场中,零售商所交的保费仅用来补偿损失:
因此,零售商的利润表达式可简化为:
![]()
引理4-3.关于银行的下侧风险约束,我们有:
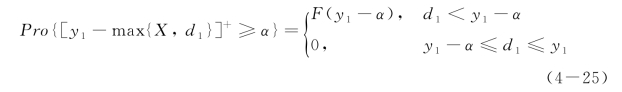
当零售商的投保水平大于临界值y 1-α时,保险公司转移了银行所有的损失风险,从而使银行下侧风险约束条件为松弛约束条件。当零售商的投保水平低于临界值y 1-α时,银行承担的损失风险关于零售商的投保水平递增。引理4-3对最优投保水平的决策起到关键作用。
命题4-4.存在唯一的临界值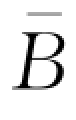 (θ)<
(θ)<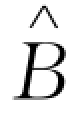 使得当零售商的资金水平低于
使得当零售商的资金水平低于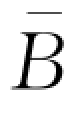 (θ)时,其选择购买保险,此种情况下,
(θ)时,其选择购买保险,此种情况下,
(1)零售商的最优订货与投保的联合决策(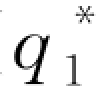 ,
,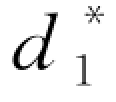 )由下面的方程组确定:
)由下面的方程组确定:
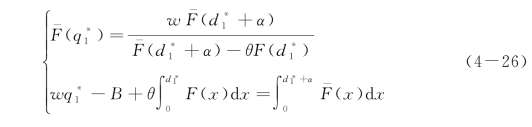 (www.daowen.com)
(www.daowen.com)
(3)零售商的最优订货量关于自有资金水平递减,而最优投保水平关于自有资金水平递增;银行设定的最优贷款利率关于零售商的资金水平递增。
考虑一种特殊情形:θ=0。基于表达式(4-26),容易得到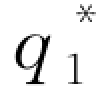 =
=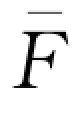 -1(w)。由此可见,当银行和保险公司均处于完全竞争的金融市场时,零售商的最优订货量为无资金约束下的最优订货量。而对于θ>0情形,显然
-1(w)。由此可见,当银行和保险公司均处于完全竞争的金融市场时,零售商的最优订货量为无资金约束下的最优订货量。而对于θ>0情形,显然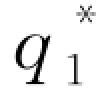 <
<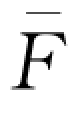 -1(w)。进一步地,考虑到零售商的最优订货量
-1(w)。进一步地,考虑到零售商的最优订货量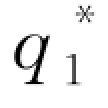 关于其自有资金水平B递减,因此必有
关于其自有资金水平B递减,因此必有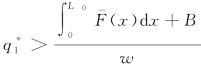 。由此可见,资金受约束的零售商可通过购买信用保险增加订货数量。然而,考虑到自身资金状况及保险公司的运营成本,零售商不会无条件地购买保险。特别地,当零售商的资金水平高于临界值B-(θ)时,零售商没有动机购买信用保险。
。由此可见,资金受约束的零售商可通过购买信用保险增加订货数量。然而,考虑到自身资金状况及保险公司的运营成本,零售商不会无条件地购买保险。特别地,当零售商的资金水平高于临界值B-(θ)时,零售商没有动机购买信用保险。
下面用数值分析对命题4-3和命题4-4进行验证。
算例4-4:假设市场需求服从均值为200的指数分布,供应商的批发价w=0.7,银行的风险厌恶系数(α,β)=(2,0.1),保险公司的风险负载因子θ=0.2。通过计算,零售商购买保险时的临界资金水平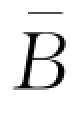 (θ)=1 6.57,银行进行下侧风险控制时的临界资金水平
(θ)=1 6.57,银行进行下侧风险控制时的临界资金水平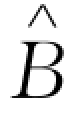 =28.15。零售商的资金水平对其最优订货量的影响如图4-5所示。
=28.15。零售商的资金水平对其最优订货量的影响如图4-5所示。
图4-5(a)中第一条虚线左侧的区域表示零售商的融资规模受到银行下侧风险的约束,零售商选择购买保险;第一条虚线与第二条虚线之间的区域表示零售商的融资规模受到银行下侧风险的约束,但零售商不购买保险;第二条虚线右侧的区域表示零售商的融资规模不受银行下侧风险的约束,零售商不购买保险。
首先,从图4-5(a)可以看出:当零售商的融资规模受到银行下侧风险约束时,零售商的最优订货量随着自有资金水平的增加而增加,当零售商的融资规模不受银行下侧风险约束时(即银行可视为风险中性),零售商的最优订货量与其自有资金水平无关。这是因为在下侧风险约束下,给定银行设定的最大融资规模,零售商的资金水平越高,订货量越大;当零售商的融资规模不受银行下侧风险约束时,由于银行处于完全竞争的金融市场中,因此零售商的运营决策不受自身资金水平的影响,此时,零售商的最优订货量为无资金约束下的最优订货量。进一步可观察到,零售商在下侧风险约束区域的最优订货量总是低于其在无下侧风险约束区域(即风险中性区域)的最优订货量。这说明在信息对称环境下,银行的风险规避因素会给零售商带来负效益。
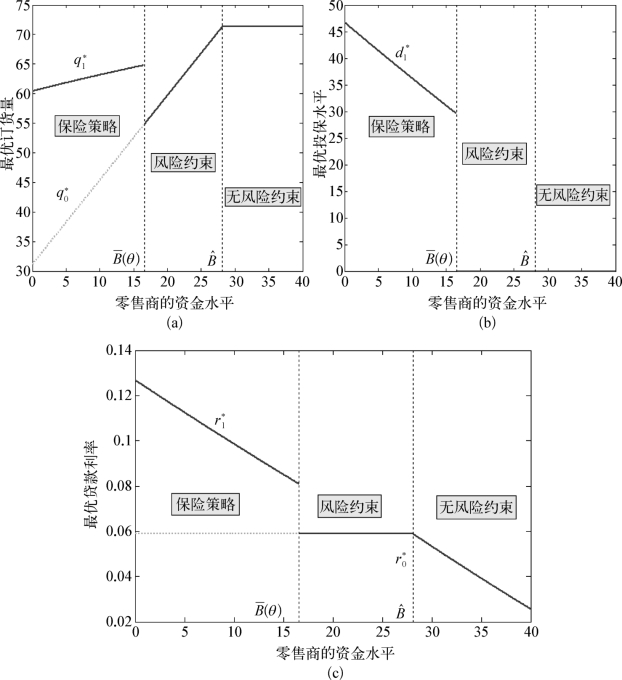
图4-5 信息对称情形下零售商的资金水平对最优决策的影响
其次,分析零售商的资金水平对最优投保水平的影响。从图4-5(b)可以看出:当零售商的资金水平低于B-(θ)=1 6.57时,零售商选择购买保险,此时最优投保水平关于零售商的资金水平递减,与命题4-6的结论一致;当零售商的资金水平高于B-(θ)=1 6.57时,考虑到投保成本及银行的风险厌恶程度,零售商没有动力购买保险,因此,最优投保水平为零。
最后,分析零售商的资金水平对最优贷款利率的影响。从图4-5(c)可以发现:在保险购买区域,即第一条虚线的左侧,购买保险情形下的最优贷款利率关于零售商的资金水平递减,同时高于不购买保险情形下的最优贷款利率,即![]() 。显然,这与通常的直觉并不一致,产生分歧的原因在于,我们假设银行根据下侧风险约束控制零售商的融资规模,当零售商不购买保险时,银行通过下侧风险约束将零售商的融资规模控制在一定水平上,使得对应的贷款利率也保持不变;而当零售商购买保险后,其融资规模得到扩大,银行有动机提高贷款利率以作为对自身面临的风险的补偿。类似地,当零售商的资金水平足够高,如图4-5(c)所示,当B>
。显然,这与通常的直觉并不一致,产生分歧的原因在于,我们假设银行根据下侧风险约束控制零售商的融资规模,当零售商不购买保险时,银行通过下侧风险约束将零售商的融资规模控制在一定水平上,使得对应的贷款利率也保持不变;而当零售商购买保险后,其融资规模得到扩大,银行有动机提高贷款利率以作为对自身面临的风险的补偿。类似地,当零售商的资金水平足够高,如图4-5(c)所示,当B>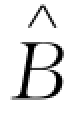 =28.15时,零售商的订货量保持在
=28.15时,零售商的订货量保持在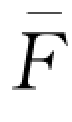 -1(0.2)=71.3的水平上,使其融资规模随自有资金水平的增大而减少,对应的贷款利率也随之降低。
-1(0.2)=71.3的水平上,使其融资规模随自有资金水平的增大而减少,对应的贷款利率也随之降低。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

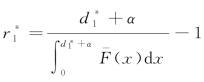 。
。





