引理3-1的证明:

命题3-1的证明:

引理3-2的证明:

基于表达式（3-8），当δw-c≥0时，πS≥0总成立。因此根据供应商的效用函数的定义，即式（3-1）可得此种情况下：

E[u（πS）]＝E（πS）

而当δw-c＜0时，可发现若X≥y L，则πS≥0；若X＜y L，则πS＜0。注意到y L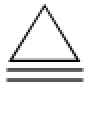（c-δw）q+y b，因此式（3-8）等价于：

基于式（3-1）并注意到δw-c＜0，因此：

命题3-2的证明:

构造Lagrange函数：

对L（y s，y b，u 1，u 2）分别关于y s，y b，u 1和u 2求一阶偏导数，得到：

可以写出KKT条件：

此时，根据式（3-29）和式（3-30），可得：

另一方面，对式（3-32）两边分别关于y b和y s求导，可得：

进而结合式（3-33）并对式（3-32）整理得到：

（2）u 1＝0和u 2＞0。

下面说明该情形不可能存在，用反证法。假设u 1＝0和u 2＞0成立，则根据KKT条件即式（3-30），有：

综上，只有情形（1）存在，因此情形（1）下的最优解即为（P1）问题的最优解。(www.daowen.com)

命题3-3的证明:

构造Lagrange函数：

可以写出KKT条件：

命题3-4的证明:

根据命题3-2，如果供应商通过设定信用契约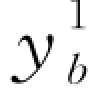（，）使得零售商需要提前支付较大比例的预付款，则供应商能够获得的期望效用为：

再根据命题3-3，如果设定信用契约（y′s，y′b），供应商获得的最优期望效用为：

引理3-3的证明:

参照Weng & Parlar（1 999），如果市场需求X服从正态分布N（μ，σ2），则下列等式成立：

其中q＝μ+σk 0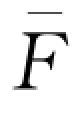，（x）为正态分布N（μ，σ2）的生成函数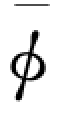，（t）为标准正态分布的生成函数。利用表达式（3-38），并结合式（3-18）不难得到式（3-1 9）。

命题3-5的证明:

将q＝（1-γ）γn/δw代入表达式（3-1 9）中，并对E（πR）关于γ求一阶导数，利用一阶必要条件即可得到命题3-5的结论。

命题3-6的证明:

当供应商提供全额的交易信用时，零售商的最优化问题为：

对E（πR）关于q求导并利用一阶必要条件即得式（3-20）。

命题3-7的证明:

类似引理3-3的证明，略。