为了更好地从运营角度刻画消费者行为，参照Weng & Parlar（1 999），假设需求市场X服从二项分布，记为X~B（n，p）。其中，n表示市场消费者的数量，p表示消费者购买产品的概率。根据假设3-4，当零售商提供价格折扣率γ，会有γf比例的消费者选择提前购买，因此零售商的订货量分为两部分：一部分用来满足提前预订的消费者需求，即γfn；另一部分用来满足常规销售阶段不确定的市场需求，即q-γfn。

注意到在预售阶段有γfn数量的消费者提前购买，因此常规销售阶段的市场消费者数量下降到（1-γf）n，使得常规销售阶段的市场需求依赖于价格折扣率γ，且服从二项分布B[（1-γf）n，p]，即X（γ）~B[（1-γf）n，p]。需要说明的是，当市场规模足够大时，二项分布B[（1-γf）n，p]逼近于正态分布。为了简化表达式，在下文中，我们只分析f＝1，λ＝1以及批发价w外生的情形，其他情形可用类似方法讨论。

在常规销售阶段，需求实现后，零售商获得的收益为min{X（γ），q-γn}，需要向供应商支付的剩余货款为（1-δ）wq。因此零售商的最优化问题为：

式（3-17）刻画了零售商的预付款约束，式（3-17）等号的左边表示零售商需要预付给供应商的货款，等号右边表示零售商通过预售策略获得的收益。换而言之，零售商通过向消费者提供预售以支付供应商的预付款。对于任意的y，z∈R以及随机变量X＞0，等式，以及当y＞z时，[min{X，y}-z]+＝min{X，y}-min{X，z}总成立。因此，零售商的目标函数等价于：

这里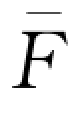（γ，x）表示正态分布的生成函数。

引理3-3.记φ（•）和ϕ（•）分别表示标准正态分布的密度函数和分布函数，则零售商的期望利润等价于：

(www.daowen.com)

需要说明的是，当δ＝0时，供应商对零售商提供全额的交易信用，此种情形下零售商不需要向消费者提供预售策略，从而使问题回归到传统的延期付款融资策略下零售商的最优决策问题。下列命题给出了零售商在全额交易信用策略下的最优订货决策。

命题3-6.当供应商向零售商提供全额交易信用时，零售商的最优订货量q∗|δ＝0满足：

考虑到表达式的复杂性，下面用一个数值算例说明预付比例δ对最优价格折扣率和最优订货量的影响。

算例3-2:假设市场规模n＝100，消费者的购买概率p＝0.4，供应商的批发价w＝0.6，供应商设定的预付款比例δ∈[0.02，1]。根据假设3-4，在预售阶段，会有100γ数量的消费者选择提前购买；在常规销售阶段，市场需求服从均值为100（1-γ），标准差为的正态分布，使用Matlab 2013a中fminbnd的命令求解最优的价格折扣率与最优订货量。

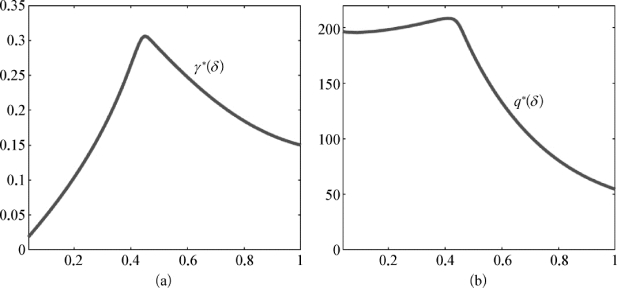
图3-6　预付比例对定价与订货的影响

（a）预付比例对最优价格折扣率的影响；（b）预付比例对最优订货量的影响

图3-6（a）和图3-6（b）分别反映了预付款比例δ对最优价格折扣率γ∗（δ）以及订货量q∗（δ）的影响。可以发现，γ∗（δ）是预付款比例δ的凹函数，当预付款比例较小或者较大时，零售商只需要提供较小的价格折扣即可满足指定的预付款要求。零售商的最优购买数量q∗（δ）关于δ的变化类似于γ∗（δ）关于δ的变化。特别地，当δ＜0.45时，q∗（δ）与γ∗（δ）关于δ递增；而当0.45＜δ＜1时，q∗（δ）与γ∗（δ）关于δ递减。这是因为当价格折扣率较低时，提前购买的消费者数量也较少，因此总的订货量也较少。