假设有一条由风险厌恶的供应商和风险中性的零售商组成的供应链，其中零售商是面临资金约束的，供应商是资金充足的。假设零售商的资金水平为零。零售商有两种主要的短期融资方式：对上游供应商延期付款融资以及向银行借贷。除此之外，零售商可通过预售策略获得短期融资。实践中，为了增加产品的销售量以及提高市场竞争力，供应商往往向零售商提供无贷款利率的延期付款（Seifert et al.，2013）。因此，对面临资金约束的零售商而言，延期付款融资相比于银行融资更有吸引力，从而使面临资金约束的零售商首先选择延期付款融资。如果延期付款融资的额度不能满足零售商的融资需求，它会再向银行或者下游消费者融资差额部分。

本章相关符号说明如表3-1所示。

表3-1　符号说明

本章基于资金约束的报童模型，即零售商以批发价w向供应商采购q单位的产品，并将产品以零售价p 0（规范化为1）销售到不确定的需求市场X，分别定义f（x），F（x）以及F-（x）＝1-F（x）为市场需求X的密度函数、分布函数和生成函数。供应商和零售商进行斯塔克尔伯格博弈，其中供应商是领导者。博弈时序如下：供应商对零售商提供信用契约（δ，w），这里δ表示零售商的预付款比例，如零售商向供应商预定q，零售商需预付δwq，剩余货款（1-δ）wq延期到需求实现后支付；基于信用契约（δ，w），零售商选择订货量q，并向银行或者下游消费者融资δwq用于支付预付款。这里，我们假设当零售商在接受信用契约（δ，w）与拒绝该契约情形下的期望收益相同时，其选择接受契约。

参照已有文献，如Kouvelis & Zhao（2012），Cai等（2014），本章使用如下假设：

假设3-1:假设需求分布服从失效率递增的性质（IFR），即失效率函数h（x）＝f（x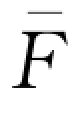）/（x）是递增的，使得广义失效率g（x）＝xh（x）也是递增的。

许多需求分布满足失效率递增的性质（Lariviere & Porteus，2001），如正态分布、指数分布、均匀分布、泊松（Poisson）分布、伽马（Gamma）分布等。

假设3-2:假设供应商具有损失厌恶性，为此引入一个损失厌恶的效用函数来量化供应商的风险厌恶性。这种效用函数在经济类及运营管理类文献中被广泛使用（Wang & Webster，2009；Zhang等，2015），具体形式如下：

这里π0是供应商利润的参照水平，不失一般性，假设π0＝0。参数λ取值范围为[1，+∞），其刻画了供应商的风险厌恶程度（后文中，我们对风险厌恶与损失厌恶不做区分），λ越大，意味着供应商越厌恶风险。特别地，当λ＝1时，供应商是风险中性的。(www.daowen.com)

假设3-3:假设零售商是有限责任的，即在需求实现后，如果零售商的销售收入无法偿还银行贷款或者供应商的剩余货款，零售商申请破产。

根据破产法，零售商优先偿还外源贷款，其次偿还内源贷款。因此，在延期付款与银行融资的混合策略中，如果零售商申请破产，则销售收入优先用来偿还银行贷款，其次是偿还供应商的剩余货款。

假设3-4:参照Weng & Parlar（1 999），在预售策略中，给定价格折扣率γ，存在γf比例的消费者选择提前购买产品。

系数f∈（0，+∞）反映了消费者对价格变动的敏感性，其中0＜f＜1表示消费者对价格变动非常敏感，而f≥1表示消费者对价格变动不敏感。

假设3-5:银行处于完全竞争的金融市场中，即银行的期望利润等于零。因此，下列等式成立：

式（3-2）中等号的左边表示银行对零售商放贷所带来的期望收益，其中δwq为零售商向银行的融资额度，δwq（1+r）表示零售商需要在销售季结束后向银行偿还的本息和，r表示银行贷款利率。式（3-2）中等号的右边表示银行的无风险收益（这里为了简化表达式，将银行的无风险利率简化为零）。为了方便起见，记y b＝δwq（1+r）。考虑到零售价被规范化为1，因此y b也表示零售商能够偿还银行贷款本息和所需要的最低销售数量。注意到y b＜q必成立（否则零售商没有向银行借贷的动机），因此式（3-2）等价于E[min{X，y b}]＝δwq。换而言之，当市场需求高于y b时，零售商能够偿还银行贷款；而当市场需求低于y b时，零售商破产。

为了简化表达式，本章假设供应商、零售商以及银行的无风险利率为零，忽略产品的残值和缺货成本。另外，为了关注面临资金约束零售商的融资与运营决策，假设供应商即刻进行生产，即供应商的生产时间为零。图3-1刻画了本章的理论结构，图3-1的左边刻画了3.3节的主要结构，图3-1的右边刻画了3.4节的主要结构。

图3-1　面向资金约束零售商的混合融资结构