（一）个人可自由支配时间、工作时间与闲暇时间

任何一个人都拥有一定的时间，比如，一天24小时，一年365天，这些时间成为个人总时间。在个人总时间中，一部分时间必须用于维持生命，如吃饭、睡觉等。个人可自由支配时间等于总时间减去维持生命所必须的时间。社会上不同的人对个人可自由支配时间的利用方式千差万别，为了揭示个人劳动力供给的一般规律，我们抽象掉这些差异，把个人可自由支配时间分为工作时间与闲暇时间两类。同样，为了研究问题的简便，定义工作时间为用于有酬工作的时间，个人可自由支配时间减去工作时间为闲暇时间。由于个人可自由支配时间是一定的，因而工作时间与闲暇时间为负相关。如何分配两种时间的比例，对劳动力供给有直接的影响。个人劳动力供给问题，实际上就是个人在工作时间与闲暇时间之间的选择问题。

（二）效用及效用函数

不同的个人，对可自由支配时间在工作时间和闲暇时间上的分配比例不尽相同，为了理解这种不同行为，需要引入效用这个概念。效用是经济学中的一个重要概念，在劳动力供给理论中，效用是指个人从工作时间和闲暇时间的组合中得到的满足程度。效用是一个主观概念，对于同一种工作时间和闲暇时间的组合，不同的人有不同的满意程度，即有不同的效用。比如，有的人愿意一天工作10小时，其他时间用于闲暇；而有的人则愿意一天工作4小时，而把更多的时间用于闲暇。正因为如此，产生了人们在分配工作时间和闲暇时间比例上的差异。

人们之所以要进行工作或闲暇时间的选择，从经济学的角度看，是因为人们从工作或闲暇中能够得到一定的满足，即效用。这样，工作、闲暇和效用之间就存在一定的联系。把这种联系用函数形式表现出来，这种函数被称为效用函数，它是用于反映效用与工作和闲暇时间之间数量关系的一种数学表达式。效用函数的一般表达式如下：

u＝f（y，h）

式中 u——效用水平；

y——工作时间所获得的收入；

h——闲暇时间。

（三）偏好与边际效用

如前所述，效用是一个主观概念，对于同一种工作时间和闲暇时间的组合，不同的人有不同的满意程度，即有不同的效用。这取决于个人的主观价值判断。所谓偏好，是指个人对某一事物的喜好。对于同样的事物，不同的个人有不同的偏好，偏好不同，同样的工作时间与闲暇时间所获得的效用也不同。

边际效用是指增加一单位货币收入（工作时间）或增加一单位闲暇时间所获得的效用。从效用函数出发，用偏微分的方法可以得到收入和闲暇的边际效用如下：

一般认为，边际效用具有递减趋势，称为边际效用递减规律。这意味着人们从每一增加的闲暇小时或收入中所增加的效用是下降的。一个人拥有的闲暇（或收入）越多，每增加一单位闲暇（或收入）中所增加的效用就越少。

（四）等效用曲线

等效用曲线是无差异曲线的一种，这里是指由取得相同效用水平的各种不同货币收入和闲暇时间组合的点所连成的曲线（见图3—1）。(www.daowen.com)

等效用曲线具有如下特征：（1）曲线离开原点越远，效用水平越高。图3—1中的三条等效用曲线的关系是U3＞U2＞U1。（2）同一个人的两条等效用曲线不能相交。相交意味着偏好的改变。（3）等效用曲线的斜率为负。说明在效用水平保持不变的条件下，要增加劳动收入，必须减少闲暇。曲线越陡峭，说明个人越重视闲暇。因为曲线越陡峭，斜率的绝对值越大，单位闲暇时间可以替代的收入越多，闲暇的价值越大。（4）等效用曲线凸向原点。上边陡峭，斜率大，下边平缓，斜率小。说明在闲暇少的时候，闲暇价值高，人们更重视闲暇；收入少的时候，单位收入可以替代更多的闲暇，收入价值高，人们更重视收入，体现边际效用递减规律。（5）不同的人有不同的等效用曲线群，体现人们的偏好的差异。重视闲暇的人，等效用曲线较陡直，重视收入的人，等效用曲线较平缓。

等效用曲线意味着收入与闲暇可以替代。

定义为等效用曲线上闲暇对收入的边际替代率，在效用函数中，效用对收入和闲暇求全微分，由于等效用曲线上的效用增量为0，移项整理即可以证明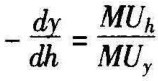，。它说明，闲暇对收入的边际替代率与闲暇的边际效用同方向变化，闲暇的边际效用越高，单位闲暇可以替代的收入越多；与收入的边际效用反方向变化，收入的边际效用越高，单位闲暇可以替代的收入越少。

（五）预算约束线与闲暇价格

预算约束线是指个人可自由支配时间的总价值量。用公式表示为：

y0＝y＋h·w

式中 y——工资收入；

h——闲暇时间；

w——闲暇价格。

以工资率作为闲暇价格，是由于人们增加一小时的闲暇，就必须减少一小时的工资。因此，工资率可以用来度量单位闲暇的价值。

将上式变形为y＝y0－h·w，它是一条直线，称为预算约束线（见图3—2）。预算约束线是个人选择效用水平的一个限制条件。由于取得较高的效用水平，必须以较多的收入和闲暇为前提条件，从预算约束线可以看出，人们的收入和闲暇都是有限的，因此，人们只能在有限的收入和闲暇的约束下来选择自己的效用水平。

图3—1 等效用曲线

图3—2 预算约束线