在实际工作中，汽车配件经营企业经常要对市场需求进行预测。市场需求预测根据收集到的统计资料、会计资料或观察值，利用数学表达式或者建立数学模型，反映需求与各种变量之间的关系，对市场需求进行预测。市场需求预测的方法主要有算术平均法、移动平均法、指数平滑法、一元线性回归法等。

算术平均法和移动平均法虽然预测精度不是很高，但因其简便实用，所以实际工作中经常采用。下面简要介绍算术平均法和移动平均法。

1.算术平均法

算术平均法是通过一组已知的统计资料或观察值求取平均数来进行预测的方法。

其计算公式为

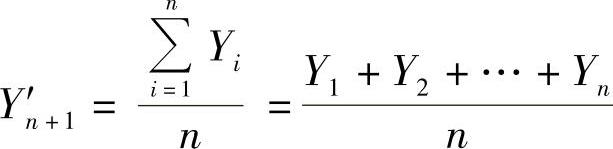
式中 Y′_n+1——第n+1期销售量的预测值；

Y_i——第i期的实际销售量；

n——所选期数。

下面举一个实例：

×××汽车配件商店前10个月离合器片的销售量依次为56、68、49、58、61、72、58、64、57、67件。利用算术平均法预测第11个月销售量为

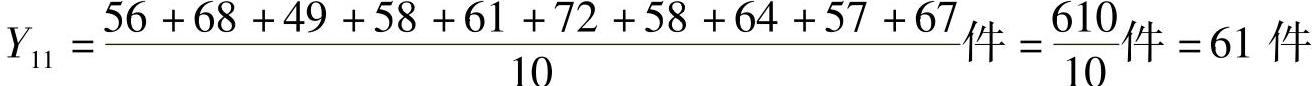
由上述计算可知，该汽车配件商店第11个月的离合器片销售量预计为61件。

2.移动平均法

移动平均法是根据已有的时间序列统计数据加以平均化，以此推断未来发展趋势的方法。所谓移动平均，就是将已有的时间序列数据分段平均、逐期移动，经移动平均后就能消除由于周期性变动或突然事件的影响因素。这种方法一般只适用于变化不大的短期预测对象。

移动平均法可分为一次移动平均法、二次移动平均法和加权移动平均法三种形式。

（1）一次移动平均法

一次移动平均法是通过一次移动平均进行预测，它按选定段的大小，对已有的时间序列数据逐段平均，每次移动一个时段。具体做法就是把最后一期的移动平均值作为下一期的预测值。其计算公式为

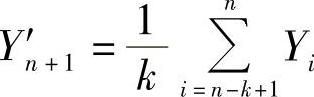
式中 Y′_n+1——n+1期的一次移动平均预测值；

Y_i——第i期的实际值；

k——移动跨期。

下面举一个实例。

×××汽车配件商店前11个月销售额见表7-1。

表7-1 ×××汽车配件商店销售额与预测值

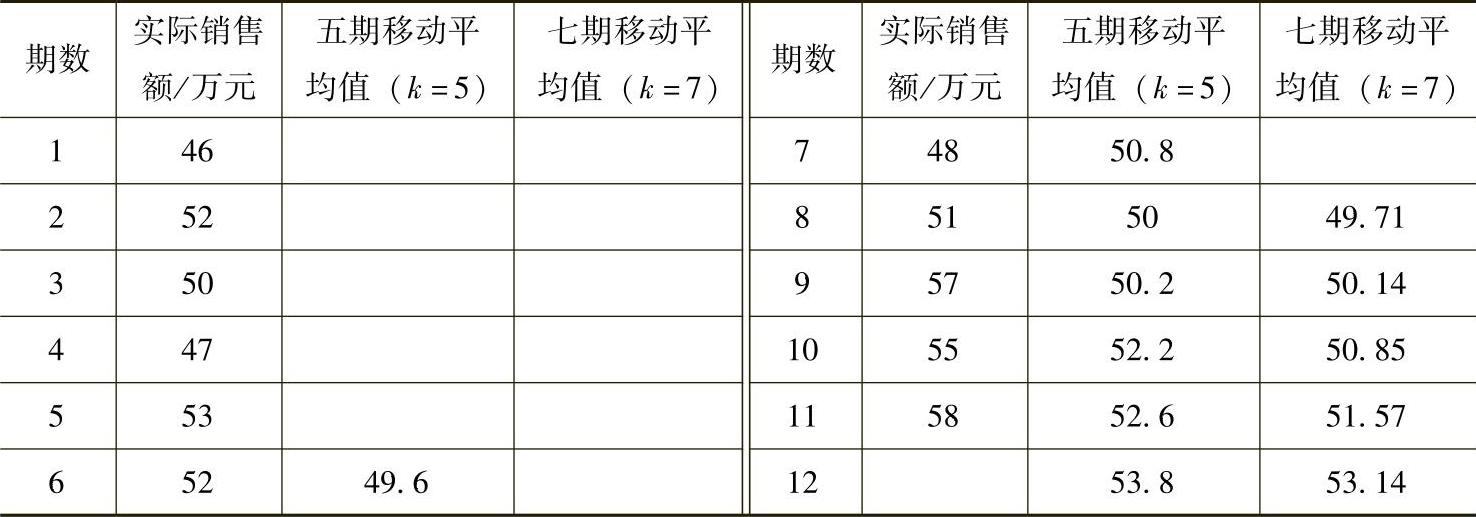
现分别以5个月和7个月作为移动跨期，预测第12个月的销售额。计算结果列于上表。

那么，当k=5时，则第12个月的预测值为

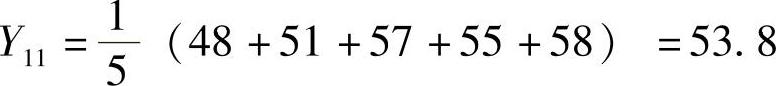(www.daowen.com)

当k=7时，则第12个月的预测值为

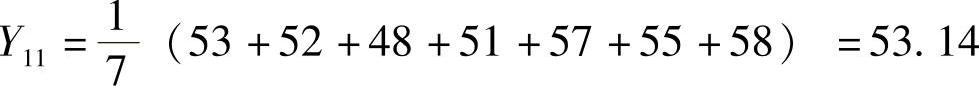
应用一次移动平均法时要注意的问题是移动跨期k的取值，k取值不同，移动平均值也不同。k取值大，预测值的趋势性比较平稳，但落后于可能发展的趋势；k取值小，移动平均值反映实际趋势较敏感，但预测值的趋势性起伏比较大。k的取值到底多大，应视具体情况而定。

（2）二次移动平均法

二次移动平均法是在一次移动平均法的基础上，为得到时间序列数据的明显线性趋势，采用相同的k值，对一次移动平均值再进行一次平均移动。

二次移动平均值的计算公式如下：

式中Y″_n+1——n+1期的二次移动平均值；

Y_i′——i期的一次移动平均值；

k——移动跨期。

仍以表7-1的数据为例，设k=3，用二次移动平均法预测结果见表7-2。

表7-2 二次移动平均法预测结果

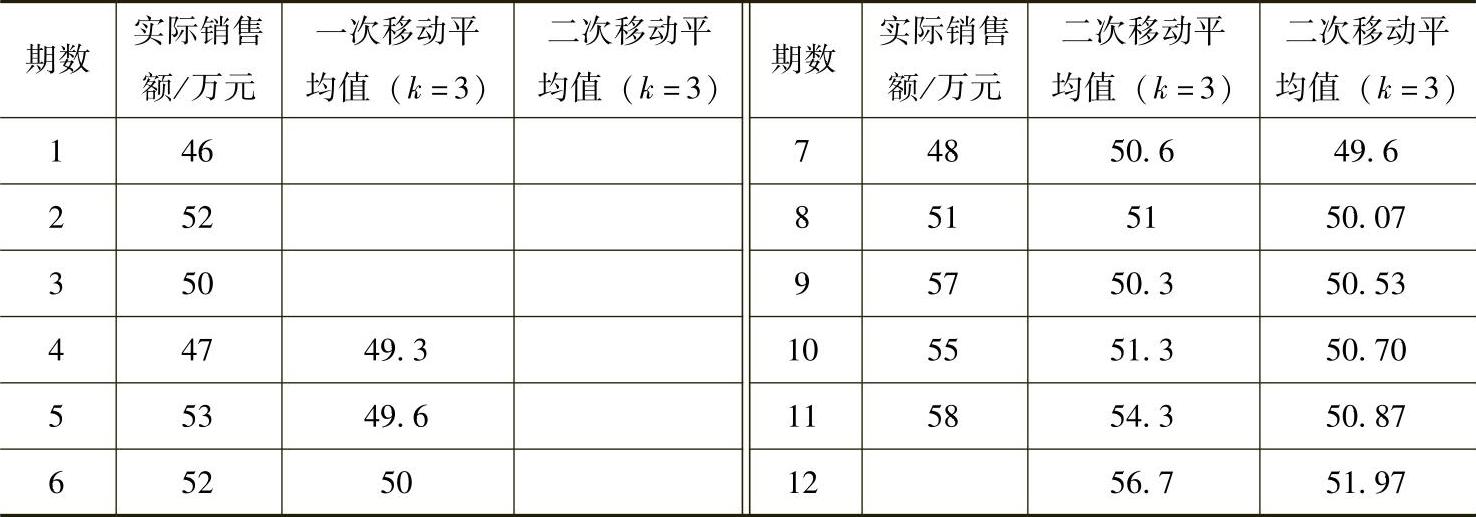
从表7-2中可以看出，用一次移动平均法预测的数值有起伏，而二次移动平均法预测的数值没有什么起伏，呈明显的线性趋势。

（3）加权移动平均法

加权移动平均法就是根据同一个移动段内不同时间的数据对预测值的影响程度，分别给予不同的权数，然后再进行平均移动以预测未来值。加权移动平均法不像简单平均移动法那样，在计算平均值时对移动期内的数据同等看待，而是根据愈是近期数据对预测值影响愈大这一特点，不同地对待移动期内的各个数据。对近期数据给予较大的权数，对较远的数据给予较小的权数，这样来弥补简单移动平均法的不足。

加权移动平均法的计算公式如下：

式中 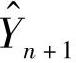——第n+l期加权平均值：

Y_i——第i期实际值：

x_i——第i期的权数（权数的和等于1）；

n——本期数；

k——移动跨期。

仍以表7-2的数据为例，用加权移动平均法求预测值。

设k=5，x₇=0.1，x₈=0.1，x₉=0.2，x₁₀=0.2，x₁₁=0.4，那么第12月的预测值为

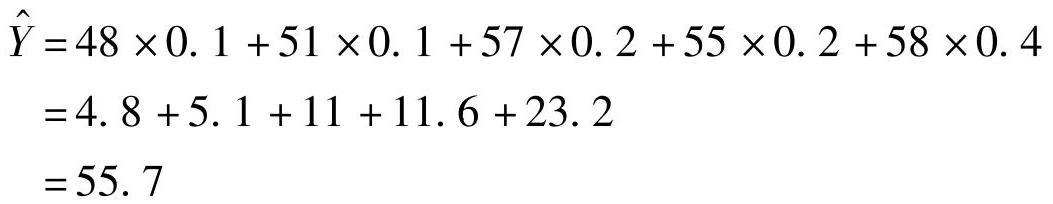
用加权移动平均法求预测值，对近期的趋势反映较敏感，但如果一组数据有明显的季节性影响时，用加权移动平均法所得到的预测值可能会出现偏差。因此，有明显的季节性变化因素存在时，最好不要加权。