下面以二维图形为例解释常见的两分类问题。首先看以下三种不同的情形。从图6-3中可以看出两类样本分布间隔较大，很容易找到一条直线将两类样本分离，这属于线性可分问题，对应的支持向量机线性可分，模型主要就是求解其最大间隔分类面。

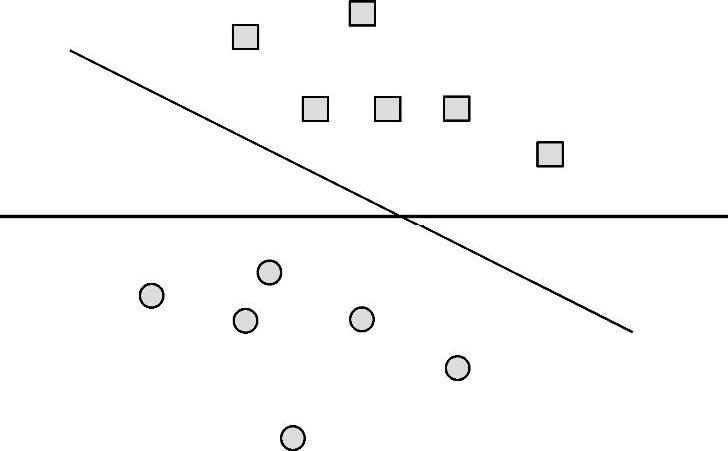
图6-3 线性可分支持向量机

图6-4描述的是线性不可分情形，用一条直线虽不能完全地分离样本集，但大致上仍能把两类样本集分离，此时仍采用线性分类机予以解决，只需在模型中加入对错分样本的惩罚项。

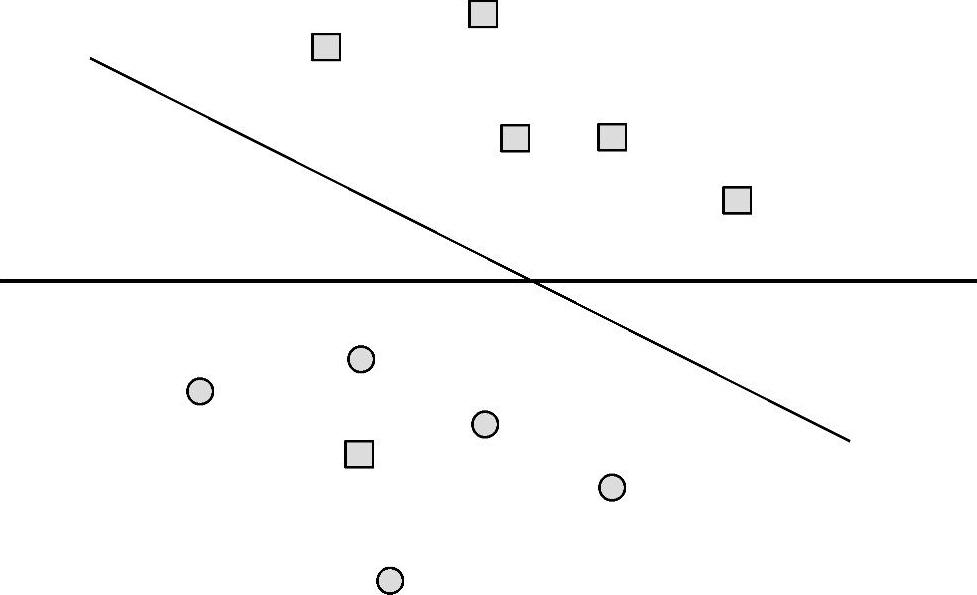
图6-4 线性不可分支持向量机

图6-5则描述了非线性可分的情形，此时用一条直线加以划分两样本集时会产生很大的误差，而若采用曲线（非线性）分类器则可顺利地分离两样本集，这就是非线性可分的问题。通过引入核函数将原先低维空间中非线性可分的样本集映射到高维特征空间中，再在高维空间中采用线性分类器将映射后的样本集加以划分。

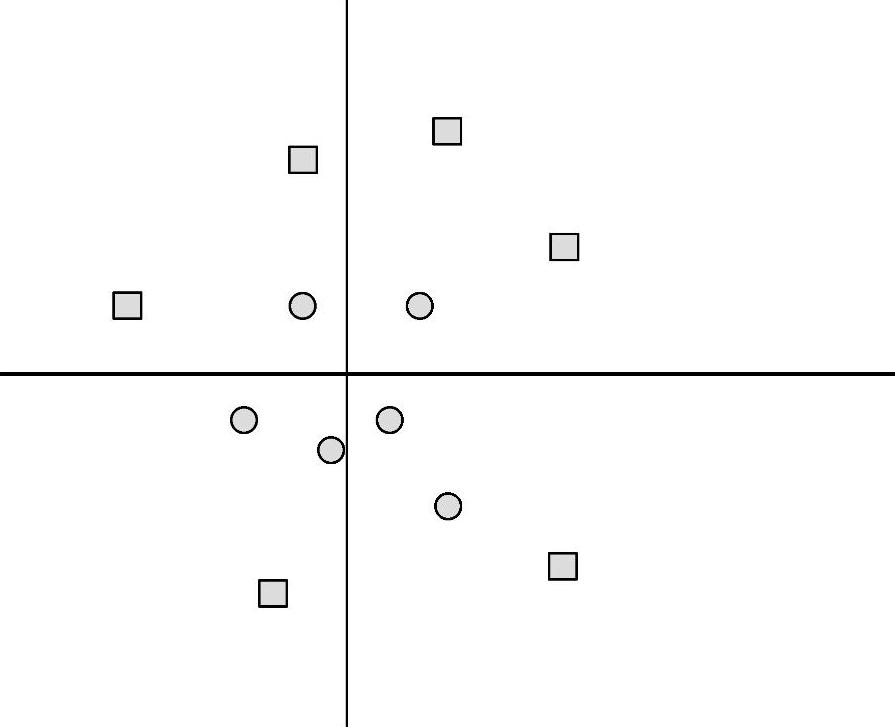
图6-5 非线性可分支持向量机

Vapink分别在1995和1998年提出C-SVM算法和v-SVM算法。为了便于比较，下面列出C-SVM算法主要的步骤和方法。

给定训练样本集{（x_i，y_i），i=1，2，…，l}，x_i∈R^d，y_i∈{−1，+1}，对于这样的分类问题，我们首先引进从输入空间Rⁿ到Hilbert空间H的变换：ϕ：Rⁿ→H，x→ϕ（x），然后在Hilbert空间H中构造原始问题：

约束条件：

y_i[（w⋅x_i）+b]≥1−ξ_i，i=1，2，…，l，ξ_i≥0 （6-2）

其中，C＞0是一个常数，它控制对错分样本的惩罚程度，控制分数机制的复杂性和不可分离点数之间的平衡，C越大表示对错误的惩罚越重。它也是算法中唯一可以调节的参数。

可以看出模型式（6-2）为典型的二次规划问题，只是问题的规模巨大，且绝大多数不具有稀疏性，使得典型的二次规划求解算法不能直接应用。支持向量分类机常用的求解方法是通过先求解其对偶问题的解，再利用该对偶问题的解来表示原始问题的解，从而确定原始分类问题的最优判别函数。采用Lagrange乘子法求解这个具有线性约束的二次规划问题，得到的对偶问题为

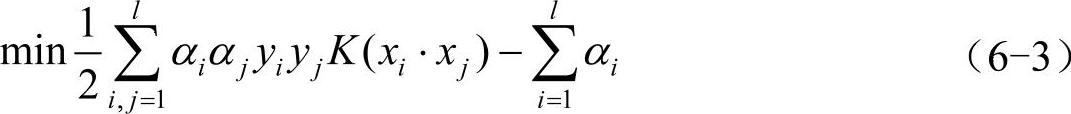
约束条件：

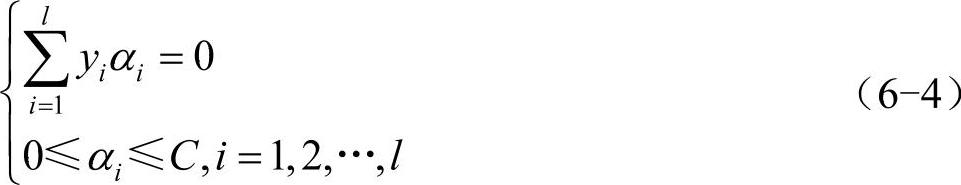
其中，K（x_i，x_j）是核函数，K（x_i，x_j）=ϕ（x_i）•ϕ（x_j），通过求解上述对偶问题得最优解α^∗=（α^∗₁，…，α^∗_l）^T，选取α^∗的一个正分量0＜α^∗_j＜C，并据此计算阈值：

b^∗=y_j-∑y_iα^∗_iK（x_i，x_j） （6-5）

最后构造决策函数：

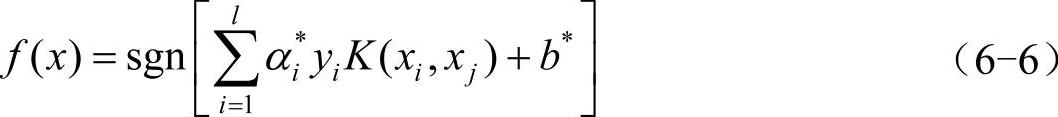
该算法称为C-支持向量分类机。

v-SVM算法要解决的原始问题为(www.daowen.com)

约束条件：

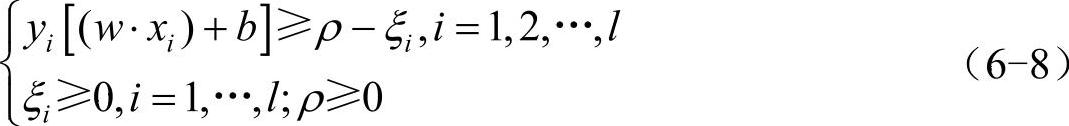
它的对偶问题为

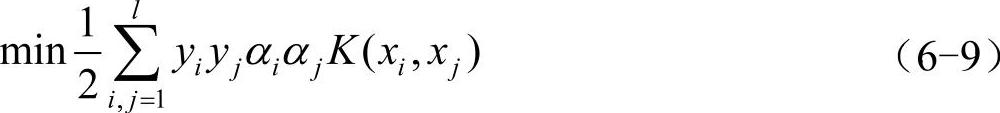
约束条件：

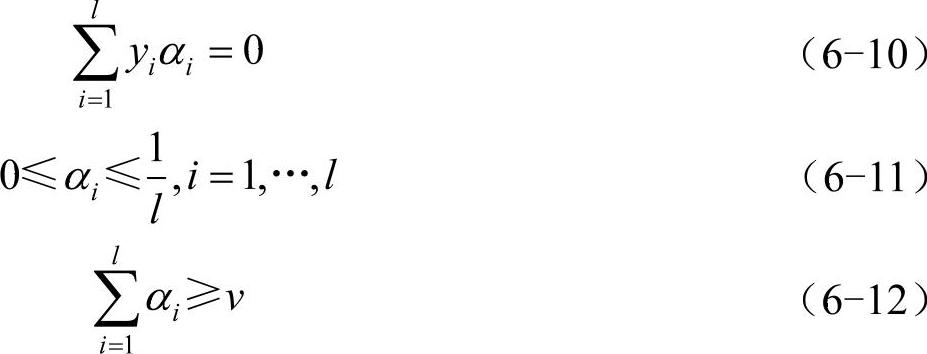
求解，即得其最优解：

α^∗=（α^*₁，...，α^*_l）^T

选取j∈S₊={i∣α^*_i∈（0，1/l），y_i=1}，k∈S₋={i∣α^∗_i∈（0，1/l），y_i=−1}，计算：

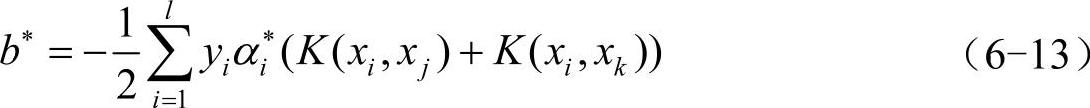
v-SVM分类中的参数v与C-SVM分类中的参数C相比，不仅具有更直观的意义，而且便于选择。

由于目前缺少连锁零售企业供应链真实门店数据，及门店风险等级评价标准。因此本节采用来源于北京工商大学水质监测实验室，其中包括pH酸碱度、溶解氧、氨氮等9项监测指标，模拟供应链门店风险等级评价数据。一共15个数据样本，选取其中12个样本作为训练集，另外三个样本作为测试集。

对样本数进行最小-最大标准化，其归一化，将原始数据规整到区间[0，1]。归一化后数据见表6-1。

表6-1 归一化后样本数据

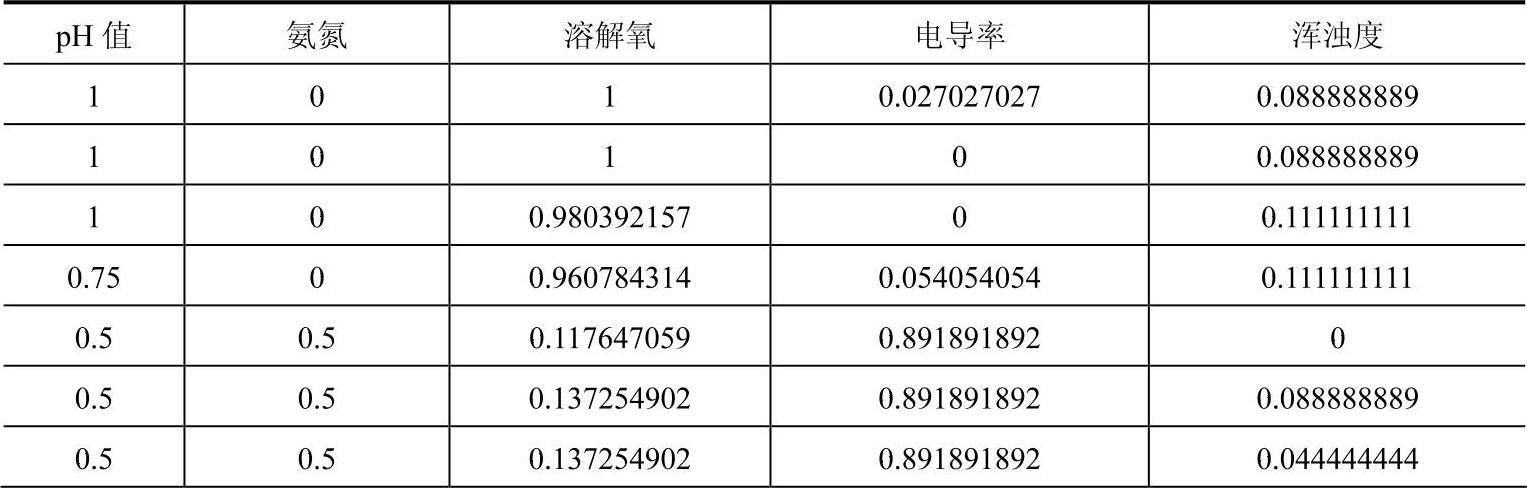
（续）

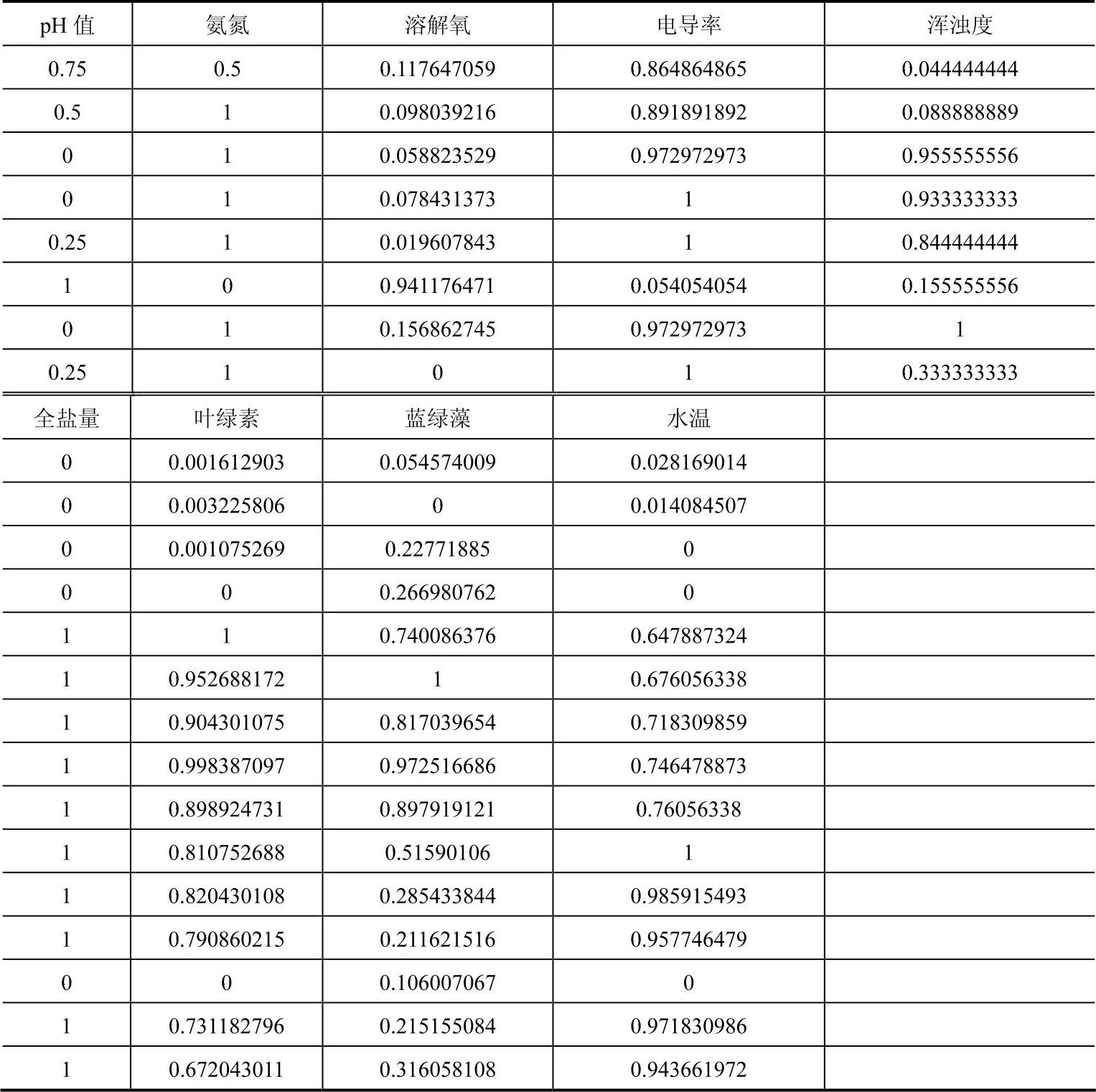
将训练集导入matlab，调用libsvm工具箱，模型选用C-SVM，核函数选用径向基函数，对于小样本分类惩罚参数c与核函数参数g均设置为1。训练完导入测试集，得到分类测试结果见表6-2。

表6-2 分类测试结果

通过实验结果可以看到SVM模型将样本13归为了Ⅳ类水，分析样本13各项指标的数据，这里只看氨氮、溶解氧、水温三项指标根据地表水环境质量国家标准中的评价标准，样本13应该归为Ⅲ类水，而综合考虑其他6项指标，尤其是浑浊度高达54，所以SVM模型将样本13归为了Ⅳ类水。

由以上研究结果可知，对于分类问题，评价标准的确定关系重大，此外在任何一个研究分类综合评价的标准里，每项指标对评价结果的影响权重都应该是不相同的，所以如何设置SVM模型里各项输入指标对连锁零售企业供应链风险评价分类结果的影响权重将成为日后继续研究的主要问题。