支持向量机（Support Vector Machine，SVM）是由Vapnik（1995）首先提出的，像多层感知器网络和径向基函数网络一样，支持向量机可用于模式分类和非线性回归。

支持向量机的主要思想是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。支持向量机的理论基础是统计学习理论，更精确地说，支持向量机是结构风险最小化的近似实现。这个原理基于这样的事实：学习机器在测试数据上的误差率（即泛化误差率）以训练误差率和一个依赖于VC维数（Vapnik-Chervonenkis dimension）的项的和为界，在可分模式情况下，支持向量机对于前一项的值为零，并且使第二项最小化。因此，尽管它不利用问题的领域内部问题，但在模式分类问题上支持向量机能提供好的泛化性能，这个属性是支持向量机特有的。

支持向量机具有以下的优点：

1）通用性：能够在很广的各种函数集中构造函数；

2）鲁棒性：不需要微调；

3）有效性：在解决实际问题中总是属于最好的方法之一；

4）计算简单：方法的实现只需要利用简单的优化技术；

5）理论上完善：基于VC推广性理论的框架。

在支持向量x_i和输入空间抽取的向量x之间的内积核这一概念是构造支持向量机学习算法的关键。支持向量机是由算法从训练数据中抽取的小的子集构成。

支持向量机的体系结构如图6-1所示。

其中K为核函数，其种类主要如下：

1）线性核函数：K（x，x_i）=x^Tx_i；(www.daowen.com)

2）多项式核函数：K（x，x_i）=（γx^Tx_i+r）^p，γ＞0；

3）径向基核函数：，γ＞0；

4）两层感知器核函数：K（x，x_i）=tanh（γx^Tx_i+r）。

图6-1 支持向量机体系结构

SVM是从线性可分情况下的最优分类面发展而来的，基本思想可用图6-2的两维情况说明。图中，圆点和叉点代表两类样本，H为分类线，H₁、H₂分别为过各类中离分类线最近的样本且平行于分类线的直线，它们之间的距离叫作分类间隔（margin）。所谓最优分类线就是要求分类线不但能将两类正确分开（训练错误率为0），而且使分类间隔最大。前者是保证经验风险最小（为0），后者是为了使置信风险最小，从而使实际风险最小，这是保证结构风险最小化原则的具体实现。推广到高维空间，最优分类线就成为最优超平面（Optimal Hyperplane）。

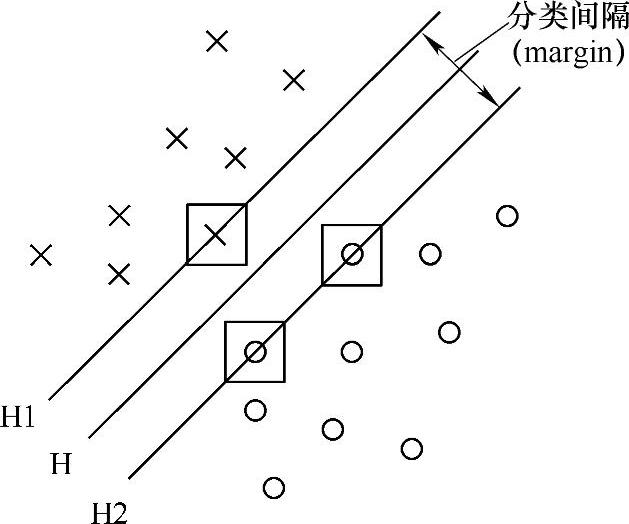
图6-2 线性可分情况下的最优分类线

分类的作用和根本目的在于，面对某一具体事物时将其正确地归于某一类，然后用同一种方法去处理同一类中的不同事物。将某一事物正确归入某一类的方法即分类方法，研究分类方法首先要确定分类标准，而对任何事物都不存在纯客观的分类标准，任何分类都带有主观性，因此对不同的分类标准会产生不同的分类方法。

支持向量机是针对模式识别问题提出来的，它的理论最初来自于对数据分类问题的处理。对于数据分类问题，如果采用传统的神经网络方法来实现，其机理可以简单地描述为，系统随机产生一个超平面并移动它，直到训练集中属于不同分类的点正好位于平面的不同侧面。这就决定了用神经网络方法进行数据分类最终获得的分割平面将相当靠近训练集中的点，从而出现“过学习”现象，造成神经网络方法的泛化性能较差。因此在SVM方法中引入了最优超平面，寻找一个满足分类要求的分割平面，并使训练集中的点距离该分割平面尽可能远，也就是使分割平面两侧的空白区域最大。

SVM方法中的大部分算法都是针对分类和预测这两类问题提出的。随着对支持向量机研究的深入，许多研究人员提出了一些支持向量机的变形算法，按照他们的算法结构特征归纳为如下系列，如C-SVM系列、v-SVM系列、W-SVM（weighted SVM）系列、LS-SVM（least-square SVM）和One-class SVM等算法。这些算法主要是通过增加函数项、变量或系数等方法使公式变形，产生出各种有某一方面优点或者一定应用范围的算法。下文中将着重介绍C-SVM系列与v-SVM系列的分类算法。