门店需求来自于市场的变化，反映消费者选择商品的情况，对商品来说分为独立需求和相关需求。独立需求是指客户对某种库存商品的需求与其他种类的商品无关，表现出对这种商品需求的独立性；而对于相关需求，客户对任一商品的需求则是对其他商品直接需求的结果，通常属于零部件的需求。举例来说，零售门店所销售的大部分成品以及商店运作所需资源均属于独立需求，但工厂生产成品所需的零部件与原料是相关需求。独立需求与相关需求有着很大的区别，前者一般受市场环境等随机因素的影响，具有不确定性和波动性强烈的特点，其表现是人为无法估计的变化特征，因此独立需求量只有通过预测统计才能得到，也就是根据分析历史资料得到，而后者是受到市场等外部因素和相关产品需求两个因素的影响，具体方法是需要从独立需求中推导出来关系，再推导出来的相关规律自动地计算出具有相关需求特点的商品需求量。

从企业管理的角度来看，企业自身不能控制独立需求的随机性变化，因为独立需求只随市场变化。独立需求与产品的其他信息，例如库存信息、订货状况、配送网络、生产计划都没有关系，在零售门店消费者对日用品、食品等产品的需求都是由每个消费者根据自身的需求决定的。在连锁零售企业中销售的常规产品都显现出这种特性。门店所销售的商品间相对独立，一般没有相关性，是面对市场大众化消费者的，而消费者挑选商品的随机性很强，不容易确定一个消费者选定一种商品同时选择另一种的概率，因此本文在针对连锁零售企业门店所普遍面临独立需求市场，而选择了对独立需求商品的预测研究。

与传统统计学相比，统计学习理论（Statistical Learning Theory，SLT）是一种专门研究小样本情况下数据分析的理论。V.Vapnik等人从20世纪六七十年代开始致力于此方面研究，到90年代中期，随着其理论的不断发展和成熟，也由于神经网络等学习方法在理论上缺乏实质性进展，统计学习理论开始受到越来越广泛的重视。

我国早在20世纪80年代末就有学者注意到统计学习理论的基础成果，但之后较少研究。直到1995年，清华大学的张学工教授对统计学习的理论系统地引进后才又逐渐为人们所关注，并在实用算法、设计和实现方面已取得丰硕的成果。统计学习理论是建立在一套较坚实的理论基础之上的，为解决有限样本问题提供了一个统一的框架，能将很多方法纳入其中，有望帮助解决在小样本数据分析问题中的难题。同时，在这一理论基础上发展了一种新的通用学习方法——支持向量机（SVM），它在处理小样本数据显现了优于其他方法的性能，成为继神经网络研究之后的研究热点。1999年，Vapnik对统计学习理论和SVM进行系统地回顾^[50]；1997年，Vapnik、GolowishS、SmolaA系统地阐述了SVM在函数拟和、回归估计、信号处理方面的应用^[51]；1998年，BurgesC.J.C介绍了SVM在模式识别、数据挖掘、知识发现方面的应用；2003年，MeyerD对SVM的分类和回归特性进行分析。SVM显示良好的优越性。

对于样本集：（x_i，y_i），i=1，…，n，x∈R^d，y∈{−1，1}，支持向量机的算法归结为下面的二次规划问题：

利用Lagrange优化方法可以把上述规划问题转化为对偶形式：

其中，。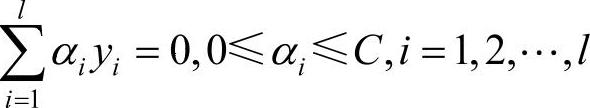

根据最优化理论，只有少量样本的α_i不为零，即为支持向量，这就是支持向量机名称的由来。用满足Mercer条件的核函数K（x_i，x_j）来代替内积运算（x_i，x_j），可实现线性算法的非线性化。(www.daowen.com)

目前对支持向量机的研究可归结为几个大的方向：

1）提高SVM的计算速度，便于处理大规模问题，如序列最小化算法，如Scholkopf和KnirschP提出缩减集方案等；

2）利用最优化技术改进支持向量机形式，简化计算过程，如线性SVM，以及Suykens JAK、Vandewalle等提出最小二乘SVM等；

3）依据结构风险最小化原则和支持向量机的某些思想提出的新的算法，如Scholkopf等提出的v-SVM，及Manga-sarian等提出的广义SVM等算法；

4）利用结构风险最小原则、核思想和正则化技术等改造传统的线性算法，构造出相应的核形式，目前核形式的支持向量机已经成为最新的研究热门。Smola较早对核形式问题进行研究，David V对当前SVM的核形式技术进行总结。

支持向量机中基于核的学习方法已在许多实际的应用领域中表现出令人振奋的技术性能，目前对它的研究正方兴未艾，新的算法不断地被提出，成为支持向量机研究的最新热门。