在连锁零售企业供应链中，无论是制造商还是供应商、零售商，都要追求资金的最快周转，都与库存管理的水平有极大的关系。因此，在整个供产销环节中，库存成为一个关键性的因素。

一般来讲，人们设置库存的目的是为了防止短缺，但在供应链管理环境下，库存不再是维持生产和销售的必然选择，而是作为一种平衡供应链的机制或可认为是一个缓冲器。通过加强库存控制，来提高供应链的系统性和集成性，增强企业的敏感性和对市场的反应能力。当然，它同时还具有分摊订货费用、缩短订货提前期、稳定生产、防止生产中断及快速满足用户需求的作用。然而，尽管库存出于种种考虑而存在，但它其实是一种无奈的结果。库存是由于人们无法预测未来的供需变化，才不得已采取的应付外界变化的手段，也正是因为人们无法使所有的工作都做到尽善尽美和确有把握，才产生一些人们并不想要的冗余和囤积。因此，供应链管理的终极目标就是要实现供应链上的供应商、制造商和零售商的零库存，其库存控制的目的就是要在满足顾客服务要求的前提下，通过对企业库存水平的控制，力求尽可能降低库存成本，提高物流系统的效率，以增强企业的市场竞争力和快速反应能力。但是传统的库存控制方式很难满足企业的现实要求，相对供应链管理环境下的库存控制而言，传统库存控制主要是解决两方面的问题，即“订货量”和“订货时间”的问题。

“订货量问题”就是确定一次进货的数量，以尽可能降低由订货费用与储存费用构成的库存总费用问题。订货费用与储存费用之间存在着矛盾，小批次、大批量订货意味着订购费用的降低和储存费用的增加。“订货时间问题”是确定合理的订货时间以降低储存费用并防止缺货的问题。减少商品库存时间与防止缺货也是一对矛盾，过早订货会增加商品库存时间，从而导致库存费用的增加；反之，又会发生缺货现象，从而导致企业经济效益和信誉损失。因此，寻找最佳订货量与最佳订货时间就成为库存控制的关键问题。

考虑供应链中简单的生产订货问题，订货时间固定，而订货量可以预先优化推导出来。为对应外部不确定需求，企业既可以选择自己生产产品，也可以通过外部第三方订货（如在线市场）来满足。其中，企业自己生产的部分考虑了生产时间滞后，并认为是不确定的。

不确定环境下的供应链生产订货动态模型为

式（5-38）为供应链生产订货库存的标量方程，该系统采用偏差描述，所谓偏差量即系统实际运作量与标称量之差。其中状态变量x_k表示为供应链在k时刻的库存。u_1，k为k时刻第三方供应商提供的订货量，为控制变量；u_2，k为k时刻制造商提供的生产订货量，为控制变量；这里考虑了制造商生产时的时滞作用，u_2，k-τ为制造商滞后提供的生产订货量；d_k为k时刻需求，为外部输入，是不确定变量；时滞参数τ有一个默认约定，即τ的取值应该确保系统的控制是稳定的。

供应链生产订货部分的运作成本为(www.daowen.com)

其中，z_k为k时刻供应链生产订货部分的运作总成本；c_h、c_o和c_m分别为确定性库存成本、订货成本和生产成本；Δc_h、Δc_o和Δc_m分别为不确定性成本。

将式（5-38）和式（5-39）写为矩阵参数形式，即

式（5-40）描述了一个供应链生产订货动态系统，其中状态方程式x_k+1中，控制时滞和外部输入是不确定的。输出方程z_k中，成本参数是不确定的。

供应链生产订货动态系统，实际上就是考虑在生产时滞、成本参数等不确定条件下，等到一个供应链稳定的生产订货控制策略，这就是所要研究的系统的鲁棒H∞控制。

供应链鲁棒H∞控制的意义是通过依据当前库存x_k推导出合适的生产订货控制u_k，抑制供应链的不确定性，使得供应链的运作总成本z达到一个较为理想的水平。γ则是供应链对于上述扰动的抑制程度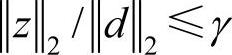，，γ越小，系统的性能越好。这一结果相当于供应链从需求d_k到输出成本z_k产生的牛鞭效应，即外部输入需求d的波动放大效应传导到输出成本z时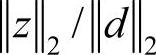，将会越来越小。应用鲁棒H∞控制策略，将得到在参数、系统时滞和外部输入扰动条件下的生产订货控制u_k，抑制牛鞭效应，并且使供应链运作成本达到一个相对小的结果。

采用LMI方法求解鲁棒H∞控制策略的过程，实际上是一个寻优过程，因此衡量系统性能的γ是人为设定的，不同的γ值所得到的控制策略也不相同。当对系统性能提出很高要求时，即γ很小，采用LMI方法很有可能无法找到可行解。尽管如此，解决该类鲁棒问题LMI方法依据不失为一种好的求解方法。