鲁棒控制（RobustControl）方面的研究始于20世纪50年代。在过去的20年中，鲁棒控制一直是国际自控界的研究热点。所谓鲁棒性，是指标称系统所具有的某一种性能品质对于具有不确定性的系统集的所有成员均成立，如果所关心的是系统的稳定性，那么就称该系统具有鲁棒稳定性；如果所关心的是用干扰抑制性能或用其他性能准则来描述的品质，那么就称该系统具有鲁棒性能。

连锁零售企业供应链系统是由多个作为自治实体的供应商、制造商、分销商、零售商的连续性供应、生产、销售活动和物流服务企业的离散性运输活动相互作用而组成的混合系统。其中不考虑生产环节，从运输配送开始到销售，大部分环节可以看作离散事件系统进行建模与仿真。这样，就可以用离散系统的数学模型来描述。

对连续系统而言，系统的数学模型可以用微分方程来表示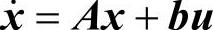，。如果把离散序列，看成连续系统中的采样结果，那么就可以得到离散系统的差分表达式，Δx=x（k+1）−x（k）。

时滞系统是指系统中存在一处或几处的信号传递有时间延迟的系统。在连锁零售企业供应链系统中生产过程、订单执行、配送等环节，物流、信息流在途过程中的传递、流动都有时间延迟。这样，连锁零售企业供应链系统本质上就是时滞系统。此外，对于一个具体环节，时滞可能由监测采样（传送）周期或过程造成，也可能由执行人员和执行元件造成，或者由它们共同造成。严格地说，连锁零售企业供应链系统中时滞是普遍存在的，只有大小的不同。时滞系统是指系统的时间滞后特性不能忽略的系统。Riddalls C E等（2002）分析了一个具有客户销售层，服务包装层，生产制造层，原料供应层等的多层供应链系统，研究表明时间滞后明显产生牛鞭效应。本质上连锁零售企业供应链系统作为一个多层离散时间系统，供应链的时间滞后，不仅包括面向顾客的订货交付时间延迟，也包括供应链中包装、生产、原料供应等物流过程的时间滞后，是一个多滞后时间常数的复杂串并联系统。

由控制理论中非最小相位系统的定义可知，时滞系统属于非最小相位系统，其稳定较差，这是由于非最小相位系统的过大的相位滞后使得输出响应变得缓慢。因此，若控制对象是非最小相位系统，其控制效果特别是快速性一般比较差，而且校正也困难。

由此可见，连锁零售企业供应链系统的典型牛鞭效应问题之所以难以有效地调控解决，从其数学模型与控制本质上分析就属于一个理论难题。

1981年，加拿大著名学者Zames在其论文中引入了H∞范数作为目标函数进行优化设计，标志着H∞控制理论的诞生。Zames考虑了这样一个SISO系统的设计问题：假设干扰信号属于某一有限能量的已知信号集，要求设计一个反馈控制器，使闭环系统稳定，且干扰对系统的影响最小。要解决这样的问题就必须在能够使闭环系统稳定的所有控制器中选出一个控制器使之相应的灵敏度函数的H∞范数最小。目前在供应链管控领域主要采用H∞理论在处理多种不确定性上有优势，鲁棒H∞控制理论是在H∞空间通过某些性能指标的无穷范数优化而获得具有鲁棒性能的控制器的一种控制理论。H∞范数的物理意义是它代表系统获得的最大能量增益。

为了辅助理解鲁棒H∞控制策略在已知系统内外部参数和扰动等不确定因素方面的作用，这里给出一些研究应用工作的主要数学结论。详细证明可参看邱若臻老师的文献与专著。

李志虎（2003），考虑一个具有时滞特性的线性离散时间系统，可得

其中，x（k）∈Rⁿ为状态变量；u（k）∈R^m为控制输入变量，z（k）∈R^p为被调输出变量；w（k）∈R^l为扰动输入变量；A、A₁、B、B₁、B_ω和C、D均为相应维数常数矩阵；ΔA、ΔA₁、ΔB、ΔB₁、ΔC、ΔD均为不确定实值矩阵函数，它们表示了系统中随时间变化的参数的不确定性；τ₁、τ₂为未知正整数，表示系统的时滞，并且满足0＜τ_i≤τ^∗，i=1，2（τ^∗已知）；ϕ（k）为系统状态x（k）的初始条件。

这个动态模型在供应链系统中应用，仅需赋予系统矩阵A、控制矩阵B、输出矩阵C、直接传递矩阵D具体代表的物理意义与参数值，也就是要注意与应用背景的结合即可。这里忽略应用背景，仅假设系统的参数不确定性具有如下形式：

其中，E_i，G_i（i=1，2，3）为已知的适合维数的常数矩阵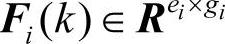；为满足下述不等式约束条件的未知函数矩阵：

其中，I_gi为g_i×g_i单位矩阵。

定义：若存在对称正定矩阵P、Q₁、Q₂以及正常数α使得对于任意（x（k），k）∈Rⁿ×R任意允许的不确定性，李雅普诺夫函数

关于k的前向差分满足：

则不确定离散时滞系统式（5-16）（u（k）=0，ω（k）=0）是二次稳定的。

对于系统式（5-16），如果存在线性状态反馈控制律：

u（k）=Kx（k） （5-21）

其中，K∈R^m×n，使得满足下列条件，则不确定离散时滞系统式（5-16）被称为是具有H∞范数界γ可镇定的。

①闭环系统是二次稳定的；

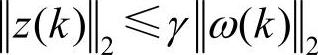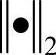②给定正常数γ，在零初始条件下，满足H∞范数约束条件，其中为标准的l₂[0，∞）范数。(www.daowen.com)

引理5-1 给定适当维数的矩阵E，G，F，且F^TF≤I，则对任意标量μ＞0，有

EFG+G^TF^TE^T≤µEE^T+µ^-1G^TG

引理5-2 给定适当维数的矩阵γ、E_b和G_b，其中γ是对称的，如果存在正常数µ_i（i=1，2，…，N），使得

其中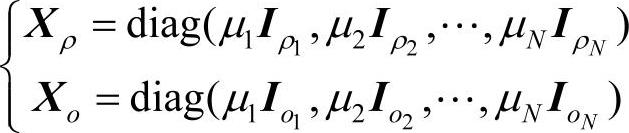

则对所有满足F^T_dF_d≤I_o的F_d=diag（F₁，F₂，…，F_N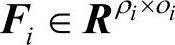），，i=1，2，…，N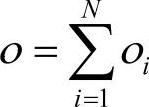，，下式成立：

具体证明从略。

定理5-1当系统式（5-16）采用反馈控制律式（5-21）时，对给定的正常数γ及容许的不确定式（5-17）、式（5-18），若存在正常数α，对称正定矩阵P、S₁、S₂以及矩阵K，使得

成立，其中A_c=A+BK+ΔA+ΔBK，C_c=C+DK+ΔC+ΔDK，则闭环系统是二次稳定的，并且具有H∞范数界γ。

定理5-2 给定正常数γ，如果存在正常数ε_i，i=1，2，…，6和对称正定矩阵Z、V₁、V₂以及矩阵W使得下面的LMI成立：

其中，

则系统是具有H∞范数γ可镇定，相应的反馈控制律u（k）=WZ^-1x（k）。

H∞鲁棒控制理论是在H∞空间（即Hardy空间）通过某些性能指标的无穷范数优化而获得具有鲁棒性能的控制器的一种控制理论。H∞空间是在开右半平面解析且有界的矩阵函数空间，其与黎卡提方程可采用如下定理解。

对于稳定传递函数G（s）=C（sI-A）^-1B，定义哈密顿矩阵：

式中，γ＞0，则下述条件是等价的：

1）；

2）H在虚轴上没有特征值；

3）黎卡提方程XA+A^TX+γ²XBB^TX+C^TC=0具有半正定解X≥0。

H∞范数代表了系统对峰值有界信号的传递特性，对应研究为持续有界干扰抑制问题。在某些场合下可以表示系统参数受扰动的情况下，依然保持H∞范数小于某个界。

H∞控制是一种具有很好鲁棒性的设计方法，可直接在状态空间进行设计，具有计算精确和最优化等优点，为具有模型摄动的不确定性MIMO系统提供了一种既能保证控制系统的鲁棒稳定性，又能优化某些性能指标的控制器设计方法。