控制理论中系统的稳定性是决定一个系统实际可用与否的首要条件，供应链的稳定性可以认为是指在外界作用下，供应链具有能够在一定范围内自我调节，从而保持和恢复原来的有序状、原有的结构与功能的能力。以Towill（1996）和Disney（2000）为代表的学者将供应链系统的稳定性作为一个独立的问题提出，引起了众多学者的重视。

考虑到保持供应链稳定性是防范供应链风险的有效途径，是弱化“牛鞭效应”的重要手段。近年来，国内外（Disney SM（2002）、马新安等（2002）、R.D.H.WARBURTON（2004））学者基于控制理论的研究，对于一些具有典型延迟环节或切换系统结构的供应链系统已明确给出了稳定性边界或稳定区间。

王晶等（2009）针对一个两级信息共享（Demand Information Sharing，DIS）供应链系统模型，应用控制理论中的劳斯判稳依据建立系统参数稳定性条件图，指出了稳定性区域的大小反映了供应链系统的抗干扰能力，供应链成员应根据供应链对稳定性和动态响应的目标调整系统参数，提高供应链的整体性能。这一研究有效地揭示了供应链系统的动态特性，能够对供应链成员的决策提出有效的管理建议。

龙建新等（2007）在供应链中借鉴和改进了控制理论的z域模型，利用系统框图识别系统的结构特征以及各个变量之间的相互关系的特性，对闭环供应链中的牛鞭效应分析，指出生产提前期和回收延迟时间对牛鞭效应有影响，且存在最优值。此方法对于仅存在信息回馈的非物资回收逆向供应链系统同样具有参考价值。

黄健等（2005）研究了一条具有多条平行分销线路的复杂供应链网络的动态稳定性。运用线性稳定性分析，得出了该模型的线性稳定性，并结合仿真得到；若将上游节点企业的库存考虑进订购策略，则将使得供应链更加不稳定。反之，若将下游企业的库存考虑进订购策略，同时若采用预期库存水平的加权平均值来调整订货率，则将使得供应链更加稳定；同时可以看出，供应链网络结构越复杂，其稳定性就会越低。

一般的实际系统都具有不确定性，当不确定性在一组给定的范围内发生变化时，如果能够保证反馈控制系统的稳定性、渐进调节和动态特性不受影响，则称该系统是具有鲁棒性的。供应链系统的运作过程中的时滞、参数和外部输入等不确定性问题，借鉴控制理论中鲁棒优化、鲁棒控制等知识对供应链不确定问题进行了研究，并取得了一定成果。

从2005年开始，东北大学黄小原团队借鉴了控制理论的一些研究方法分析供应链系统，指出了鲁棒性问题研究在供应链管理中具有重要的实践意义和理论意义。分析了供应链系统的外部联接、突发事件和内部运作不确定性的两种表现形式，而后评述和分析了供应链的不确定性模型和鲁棒运作策略，最后就供应链鲁棒性研究提出几个值得思考的问题。后续团队成员采用H∞控制方法，对供应链中的牛鞭效应进行抑制。先后建立具有供应链末端需求扰动的状态空间动态系统，建立具有供应链末端需求扰动的上游订货波动的扰动指标，以此描述牛鞭效应。而后应用H∞控制理论提出供应链牛鞭效应的控制理论方法，其本质就是考察供应链末端需求波动最差条件下，如何采取一个良好的控制策略，使牛鞭效应减到最低程度。并且以一个供应链多层时滞系统为对象进行了供应链牛鞭效应的H∞控制仿真实验，进行了仿真验证。

郭海峰等[2008]针对目前，出于环保节能等原因的考虑，已售出商品的回收、再制造等逆向物流问题与正向物流相互作用，再制造系统中的牛鞭效应的控制问题。采用H∞控制方法，提出顾客需求波动最差条件下制造商平滑生产控制策略，以抑制牛鞭效应。由仿真计算的结果可知，再制造生产产生的逆向物流加剧了供应链的牛鞭效应。

葛汝刚等[2009]结合供应链发展中的自行回收再制造和外包业务的发展，以及实际运行中需要依据成本变换控制策略的需要，设计了具有外包选择的切换信号，建立了具有外包选择的闭环供应链切换系统模型。应用切换系统控制理论，给出了控制律，并进行了仿真实验和分析。

这些研究成果对通过研究保持供应链系统的稳定对于削弱牛鞭效应、改善供应链整体绩效具有重要意义。

系统鲁棒性的提出是由于现代控制理论的许多成果在理论上很漂亮，但实际应用并不成功。主要原因是忽略了对象的不确定性，并对系统所存在的干扰信号作了苛刻的要求。

考虑如下一个对图5-4增加了扰动信号的单输入单输出（SingleInputSingle Output，SISO）系统的设计问题：对于属于一个有限能量的干扰信号，设计一个控制器使得闭环系统稳定且干扰对系统期望输出影响最小。

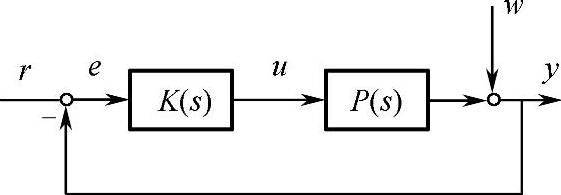
图5-4 不确定性存在的SISO闭环系统框图

图中，K（s）为控制器，w为干扰信号，r为参考输入，u为控制输入，e为控制误差信，y为输出信号。系统的开环和闭环传递函数为

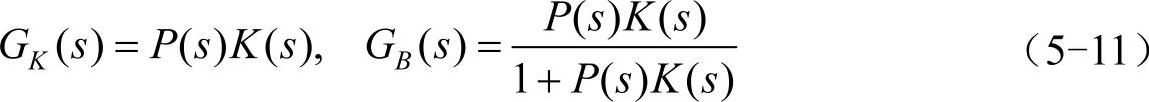
如果P（s）不够精确，具有误差表示为P（s）=P₀（s）+ΔP（s），那么相应的开环和闭环传递函数也具有误差：

G_K（s）=G_K0（s）+ΔG_K（s），G_B（s）=G_B0（s）+ΔG_B（s） （5-12）(www.daowen.com)

其中，G_K0（s）=P₀（s）K（s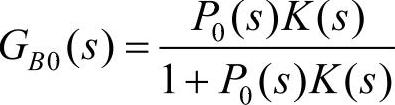），，分别为开环和闭环传递函数的标称函数，简单地推导可得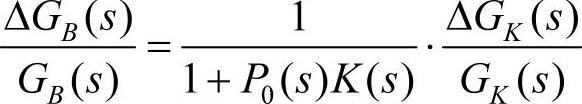，定义一个新的传递函数为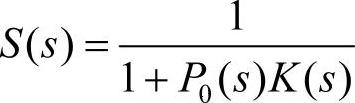：，则此函数体现了开环传递特性的相对偏差ΔG_K（s）G_K（s）到闭环传递特性ΔG_B（s）G_B（s）的增益。因此，在设计控制器K时，如果能够使S的增益足够小，即S（s）＜ε，ε为充分小正数，则闭环特性的偏差将会抑制在工程允许的范围内。

上面定义的传递函数S（s）称为系统的灵敏度函数。实际上S（s）还等于干扰w到输出的闭环传递函数，因此减小S（s）的增益就等价于减小干扰对控制误差的影响。

引入定义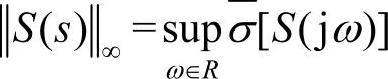，其中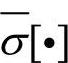表示求取对应的最大奇异值，即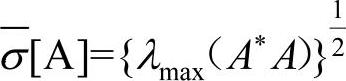，A^∗为A的共轭转置阵，λ_max为最大特征值。

鲁棒H∞控制问题即为对于给定的ε＞0，设计控制器K（s）使得闭环系统稳定且满足。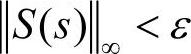

鲁棒H∞理论中考虑干扰信号是不确定的，而是属于一个可描述集：

L₂中包含的是能量有限的干扰信号。考虑抑制干扰w（t）∈L₂对系统性能的影响，为此引入γ表示干扰抑制水准的标量，计算求取控制器K使得满足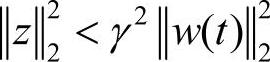，∀w（t）∈L₂，y为输出信号。定义频率特性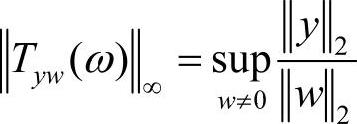：，其中，T_yw（s）由w至y的闭环传递函数，则此式等价于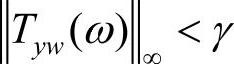，求使γ为最小的控制器K，这一过程实质就是H∞最优设计问题。

对于系统的传递函数G（s），若其在右半平面无极点，定义下面的范数为传递函数的H∞范数：

其中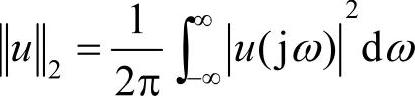，，则。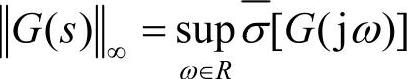

H∞鲁棒控制理论的实质是为多输入多输出（MIMO）且具有模型摄动的系统提供了一种频域的鲁棒控制器设计方法。H∞鲁棒控制理论很好地解决了常规频域理论不适于多输入多输出（Mult：-Input，Mult：-Output，MIMO）系统设计及线性二次高斯（LQG）理论不适于模型摄动情况两个难题，其计算复杂的缺点已因计算机技术的飞速发展及标准软件开发工具箱的出现而得到克服，故近十年来已成为控制理论的一个热点研究领域，并取得了大量的实际应用成果。

针对MIMO时域系统自治模型，

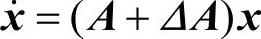，y=（F+ΔF）x，其中ΔA=EΔF，Δ为任意满足Δ^TΔ≤I的实矩阵，E、F为已知矩阵。

定理：对任意的Δ，Δ^TΔ≤I，A+EΔF稳定当且仅当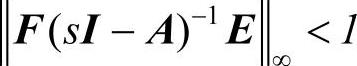，则系统的鲁棒控制问题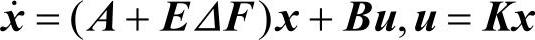

即为设计K使得A+BK+EΔF稳定，也即